26 April 2021

I have never had a computer science class. I'd say I'm behind those people who graduated in the field for 48 months. I had to spend some time trying to understand what a CS student's bookshelf is like.

Although it's said that nothing is given so freely as advice, with a wish that what I listed up here is useful not only for myself but also for people, here I'm writing this article that is meant to provide a comprehensive map.

I'd stick to OPEN DATA STRUCTURES and PROJECT EULER mentioned at the bottom of this page, and use the rest of them as supplementary resources.

P.S. 25 November 2021

All is said and done, just take the FREE LECTURES OF PROFESSOR ROBERT SEDGEWICK on Coursera.

Useful materials

🎞️🎞️🎞️ Youtube playlist containing all videos listed in this page.

Computer architecture

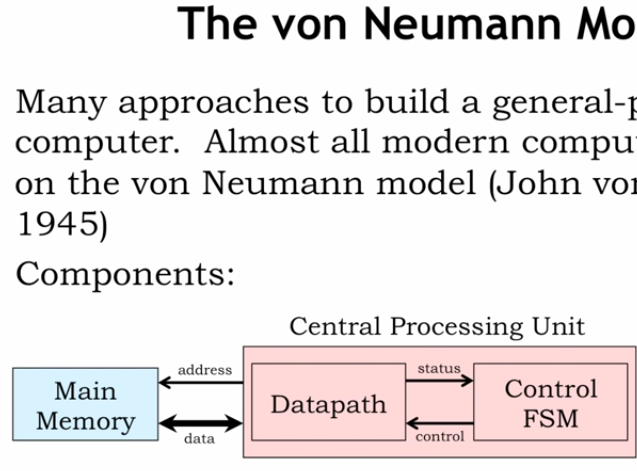
🎞️ MIT, 9.2.3 The von Neumann Model
CPUs have the dedicated ADDRESS BUS in addition to the data bus.

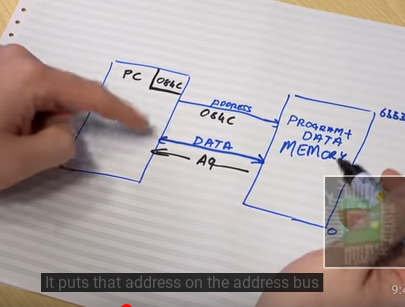
🎞️ Inside the CPU - Computerphile
Address bus (2)

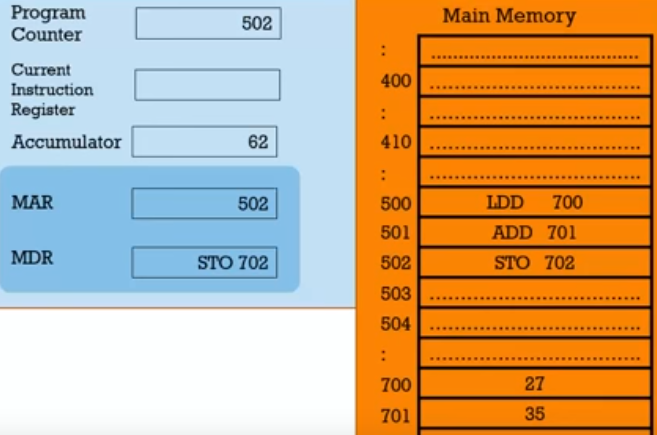
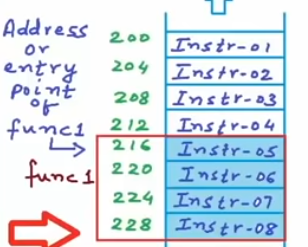
🎞️ Introduction to Von Neuman Architecture (Fetch-Decode-Execute) Cycle
Instructions LDD, ADD, STO, and data 27, 35 are stored in memory.
Addressing is the only way to tell the difference between them.
It's quite less than Javascripts' ===, the type considering equality.

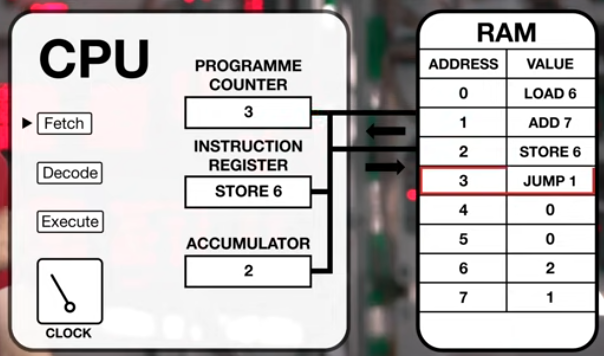
🎞️ Tom Scott, The Fetch-Execute Cycle: What's Your Computer Actually Doing?
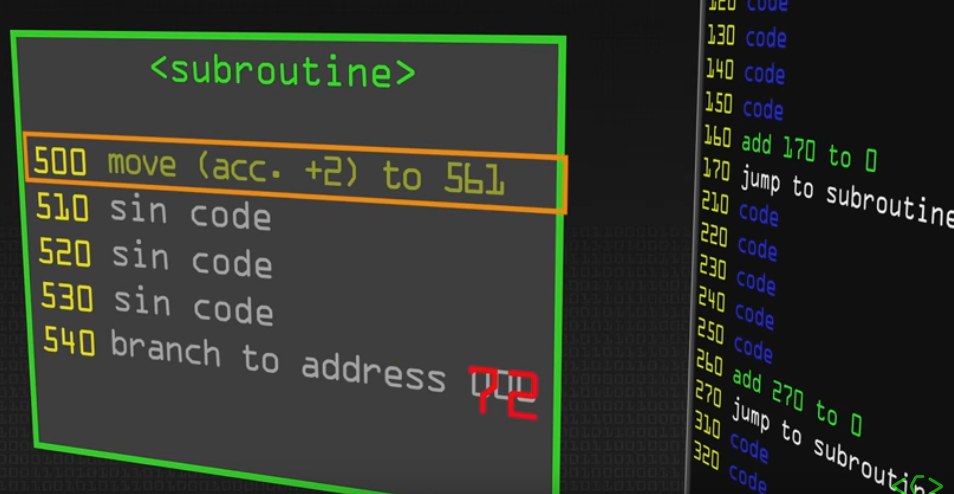
There's JUMP instruction, which will be described for the genesis of the subroutine later.

🎞️ The Calculator Wars: A video history of Japan's electronic industry (Part 3)
The bit part of the 64bit and 32bit CPU describes the addressible memory breadth. What is called usize/uintptr type, unsigned integer, 64bit length in the case of a x86_64 CPU.
Intel 4004 a 4bit processor. The capacity of an address will be mentioned in Open Data Structures as the word length.

🎞️ そろばんで３度目の日本一　西宮市の中３女子
The arithmetics with a set of circuits in CPU must be the same mechanism to a series of skills that the hands perform on a bit-wise abacus in fundamentals.

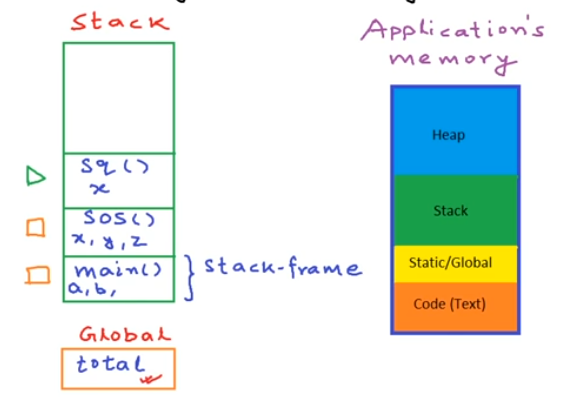
🎞️ Pointers and dynamic memory - stack vs heap
There are regions called STACK FRAMES for each function call.

🎞️ freeCodeCamp.org, Pointers in C / C++ [Full Course]
Jumping is enabled by means of the technique called function pointers, which allows us to use LOOP for example.
You might prefer to watch CS50 written below first.

• P.S. 22 November 2021
  "process is a logical container", "slice of CPU time", "process needs memory'
  🎞️ Processes and threads - Gary explains
  "system calls", "processes must be able to invoke certain routines at fixed addresses in the OS's portion of memory"
  🎞️ Operating System Basics
  "there is not only one process associated with this chromium browser"
  🎞️ Process Management (Processes and Threads)
  "event queue", "callbacks"
  🎞️ What is the JavaScript event loop really all about - Java Brains
  "Change the root directory of the current process to the specified path."
  std::os::unix::fs::chroot
• P.S. 7 December 2022
  readelf command in Linux with Examples
  Understanding the Linux /proc/id/maps File
  Position-independent code

🎞️ Wheeler Jump - Computerphile
Stories behind the subroutines

Software development

🎞️ CS50 2020 - Lecture 4 - Memory
Confirm the garbage values in memory and the undefined behaviour in C.

🎞️ CS50 2020 - Lecture 3 - Algorithms
Finding and comparison

🎞️ CS50 2020 - Lecture 5 - Data Structures
The physical restriction on the consective allocation extension, for the area is possibly already claimed by the other.

🎞️ Junmin Lee, Golang Tutorial 3 - Golang pointers explained, once and for all
Memory and the pointer in summary

Data structures and algorithms

🎞️ Fyi, MIT, Instruction-level Parallelism

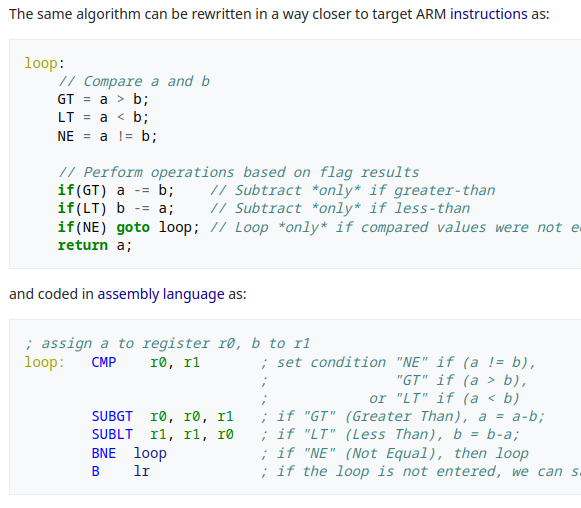
Fyi, ARM architecture - conditional execution - Wikipedia

🎞️ freeCodeCamp, Data Structures Easy to Advanced Course - Full Tutorial from a Google Engineer
Comprehensive step by step tutorial about data structures. This allowed me to be familiar with their names and ready to read books about them.

• https://github.com/williamfiset/data-structures
• https://github.com/williamfiset/Algorithms

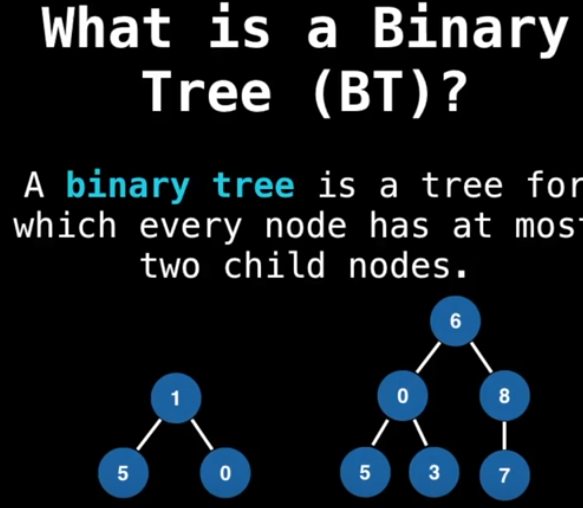
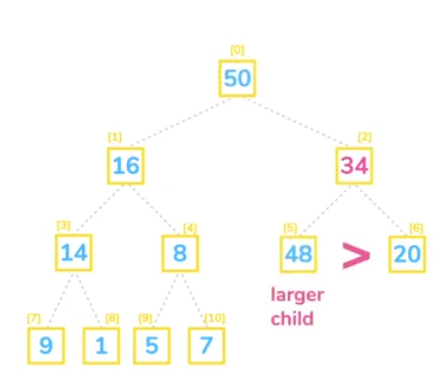
🎞️ Spanning Tree, What is Binary Heap
There is sort of confusion in nomenclature, and watching these videos by Brian from CS50 at that time helped me to understand the 8h data structure tutorial.

🎞️ Spanning Tree, What Are Bloom Filters?

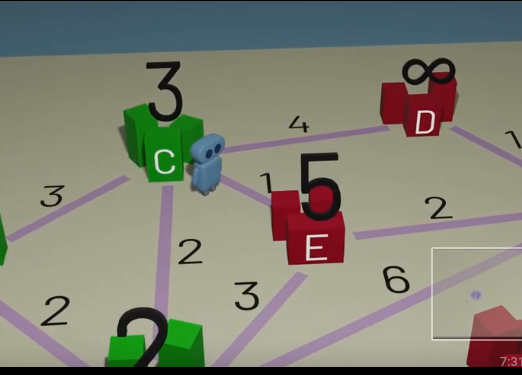
🎞️ Spanning Tree, How Dijkstra's Algorithm Works

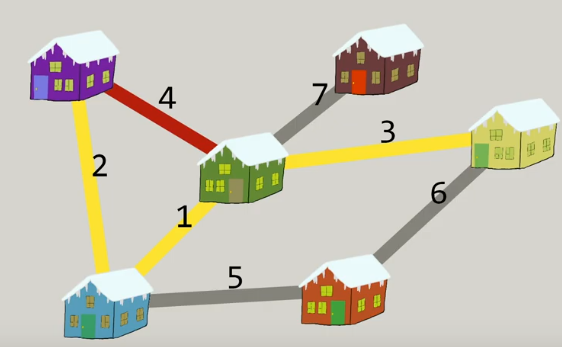
🎞️ Spanning Tree, How Do You Calculate a Minimum Spanning Tree?

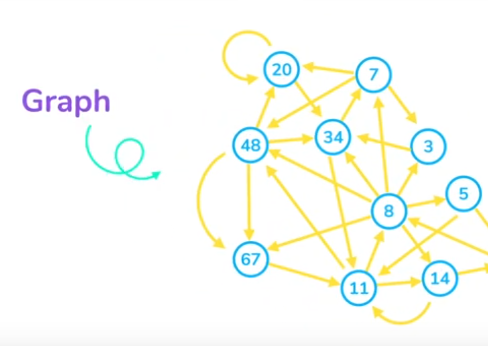
🎞️ Junmin Lee, Graph data structure and graph representation (Part 1 of 2)
It was helpful for me to watch this video at that point so as not to sink in the confusion.

🎞️ Junmin Lee, Data Structures and Algorithms in Go - Heaps

📖 Open Data Structures
It took me a while to know there was this book.

• https://github.com/patmorin/ods/tree/master/java
• https://github.com/spinute/ods-go
• https://github.com/o8vm/ods rust

📖 Introduction to Algorithms, 3rd Edition (The MIT Press)
I couldn't find this book in my shallow previous research. I append this book here on 13 June 2021.

📖 Princeton University, Algorithms (4th Edition)
It seems to me that you wouldn't want this book if you already have Introduction to Algorithms, 3rd Edition. P.S. there's a complete online course.

• 2.4 Priority Queues
• github.com/kevin-wayne/algs4

📖 Algorithms in a Nutshell: A Practical Guide 2nd Edition
I flipped through all the pages. I'd stick to Open Data Structures.
It seems to me that you wouldn't want this book if you already have Introduction to Algorithms, 3rd Edition.

Additionally, it was comprehensive too. But I'd better stick to Open Data Structures.

• Lecture Notes for Data Structures and Algorithms (School of Computer ScienceUniversity of Birmingham)

📖 WILLEY, Data Structures and Algorithms in Java, 6th Edition
In fact I read only 4 out of 15 chapters. But it was nice to know about the generics dynamic dispatch and the parameters in Java are passed by value, such as badReset(Counter c) {c = new Counter();} //reassign local name c to a new Counter.

📖 SAMS, Data Structures and Algorithms in Java 2nd Edition
I haven't read it and probably it's not required if you have Open Data Structures.

Mathematics

🎞️🎞️🎞️ Youtube playlist

🖊️ Project Euler
I solved 33 questions so far and it helped me to remember mathematics and to know algorithms.

• https://euler.stephan-brumme.com/
• https://www.nayuki.io/page/project-euler-solutions
• https://www.mathblog.dk/project-euler-solutions/
• https://www.xarg.org/puzzles/
• https://github.com/XiaoTaoWang/Project-Euler
• https://blog.dreamshire.com/category/project-euler-solutions
• P.S. 9 December 2022 ガウスとオイラーの整数論の世界　～中学入試算数が語るもの～

📖 The Concise Oxford Dictionary of Mathematics

📖 Mathematics Dictionary (5th ed) James & James

• archive.org (1949)
• 朝倉書店 数学辞典 (世田谷区図書館所蔵)

📖 Schaum's Outline of Mathematical Handbook of Formulas and Tables, Fifth Edition

• 1300 Math Formulas PDF

📖 Collins Dictionary of Mathematics, by E. J. Borowski and J.M. Borwein

Compiler design

I haven't read them but it seems there are some chapters for data structures.

📖 Advanced Compiler Design and Implementation

📖 Compilers: Principles, Techniques, and Tools 2nd Edition

Further reading...

📖 Algorithms and Data Structures, Niklaus Wirth

• Algorithms and Data Structures (1985)
• Algorithms and Data Structures = Programs (1976)

📖 Algorithms in C, Robert Sedgewick

• セジウィック:アルゴリズムC 第1~4部 ―基礎・データ構造・整列・探索 (世田谷区図書館所蔵)

📖 A Simple Introduction to Graph Theory, Brian Heinold

📖 Introduction to Graph Theory (5th Edition) Robin J. Wilson

• maths.ed.ac.uk (1996)
• グラフ理論入門 (品川区図書館所蔵)

📖 アルゴリズム辞典 1994 (世田谷区図書館所蔵)

📖 C言語による最新アルゴリズム事典 (ソフトウェアテクノロジー) 奥村 晴彦

📖 最短経路の本 (世田谷区図書館所蔵)

📖 Cracking the Coding Interview: 189 Programming Questions and Solutions 6th Edition

📖 Brilliant.org Community Wiki

Dangling pointers and the alignment of composite data

• doc.rust-lang.org/nomicon/repr-rust.html
• doc.rust-lang.org/reference/type-layout.html
• web.mit.edu/rust-lang_v1.25/arch/amd64_ubuntu1404/share/doc/rust/html/book/second-edition/ch04-03-slices.html#string-slices

Network interface controller, subnets and gateways

• en.wikipedia.org/wiki/Network_interface_controller
• docs.microsoft.com/en-us/azure/developer/terraform/hub-spoke-on-prem

P.S. 7 December 2022 📖 ［試して理解］Linuxのしくみ

PS

Data structures and algorithms might be easier than the non-pedagogical programming in a sense for its internal perfection and predictability.

I mean, I can imagine you are using Postman to check against a service that was provided by some organisation so that you can confirm the functionalities are implemented as described in their documents after experiencing irregular behaviours; you are collating the version of a Kubernetes' application in debugging for a runtime error that couldn't be detected with mock tests; or you are in a tunnel to find out idioms unheard of to write a passable Gradle script or an industrial level quality test code with the most up-to-date Mockito library with an extension that is also unheard of.

A warning says I must not click the back button in the browser. A question form doesn't have the option to choose for my answer. This kind of problem occurs regardless of using a computer or a sheet of paper.

As for me, having been stuck in quotidian affairs, I'm poor in certain things to be certified, which is not what I'm proud of. It definitely happens that you are busy with the handling of Authorization metadata of gRPC but have no chance to implement a MySQL of your own.

struct ArithmeticProgression {
    first: i32,
    last: i32,
    diff: i32,
}

impl ArithmeticProgression {
    fn arithmetic_series(&self) -> i32 {
        assert!(self.diff != 0);
        assert!(
            (self.first > self.last) == (0 > self.diff),
            "The relationship between the first element and the last element \
            with the negativity of the common difference is incoherent."
        );
        let terms = (self.last - self.first) / self.diff + 1;
        assert!(
            self.first + self.diff * (terms - 1) == self.last,
            "The length between the first element, \
            the common difference and the last element is incoherent."
        );
        (self.first + self.last) * terms / 2
    }
}

fn main() {
    let a = ArithmeticProgression {
        first: 0,
        last: 999,
        diff: 3,
    }
    .arithmetic_series();
    let b = ArithmeticProgression {
        first: 0,
        last: 995,
        diff: 5,
    }
    .arithmetic_series();
    let ab = ArithmeticProgression {
        first: 0,
        last: 999 - 999 % 15,
        diff: 15,
    }
    .arithmetic_series();
    println!("{}", a + b - ab);
    assert_eq!(a + b - ab, 233168);

    assert_eq!(
        ArithmeticProgression {
            first: 2,
            last: 14,
            diff: 3
        }
        .arithmetic_series(),
        2 + 5 + 8 + 11 + 14
    );
    assert_eq!(
        ArithmeticProgression {
            first: 3,
            last: 12,
            diff: 3
        }
        .arithmetic_series(),
        3 + 6 + 9 + 12
    );
    assert_eq!(
        ArithmeticProgression {
            first: 1,
            last: 10,
            diff: 1
        }
        .arithmetic_series(),
        (1 + 10) * (10 / 2)
    );
    assert_eq!(
        ArithmeticProgression {
            first: -10,
            last: 10,
            diff: 1
        }
        .arithmetic_series(),
        0
    );
    assert_eq!(
        ArithmeticProgression {
            first: -4,
            last: 2,
            diff: 1
        }
        .arithmetic_series(),
        -4 - 3
    );
    assert_eq!(
        ArithmeticProgression {
            first: 5,
            last: -1,
            diff: -2
        }
        .arithmetic_series(),
        5 + 3 + 1 - 1
    );
    assert_eq!(
        ArithmeticProgression {
            first: 6,
            last: 0,
            diff: -2
        }
        .arithmetic_series(),
        6 + 4 + 2
    );
    assert_eq!(
        ArithmeticProgression {
            first: 6,
            last: 2,
            diff: -2
        }
        .arithmetic_series(),
        6 + 4 + 2
    );
    assert_eq!(
        ArithmeticProgression {
            first: -6,
            last: 0,
            diff: 2
        }
        .arithmetic_series(),
        -6 + -4 + -2
    );
    assert_eq!(
        ArithmeticProgression {
            first: -6,
            last: -2,
            diff: 2
        }
        .arithmetic_series(),
        -6 + -4 + -2
    );
}

package main

import (
	"fmt"
)

func arithmeticSeries(n uint32) uint32 {
	d := 999 / n
	return n * d * (d + 1) / 2
}

func Example() {
	ans := arithmeticSeries(3) + arithmeticSeries(5) - arithmeticSeries(15)
	fmt.Println(ans)
	// Output: 233168
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg)
  }
}

function arithmeticSeries(n: number): number {
  assert(Number.isInteger(n));
  assert(Math.sign(n) === 1, "Tried a negative n or division by zero.");
  const d = 999 / n | 0;
  return n * d * (d + 1) / 2 | 0;
}

const ans = arithmeticSeries(3) + arithmeticSeries(5) - arithmeticSeries(15);
console.log(ans);
assert(ans === 233168);

struct TripleBox {
    i: u64,
    j: u64,
    k: u64,
}

impl TripleBox {
    fn shift(&mut self) {
        self.i = self.j + self.k;
        self.j = self.k + self.i;
        self.k = self.i + self.j;
    }
}

fn main() {
    let mut sum = 0;
    let mut tb = TripleBox { i: 0, j: 1, k: 1 };
    while tb.i <= 4_000_000 {
        sum += tb.i;
        tb.shift()
    }
    println!("{}", sum);
    assert_eq!(sum, 4613732)
}

struct LuckyClover {
    a: u64,
    b: u64,
    c: u64,
    d: u64,
}

impl LuckyClover {
    fn multiply(&mut self, other: &LuckyClover) {
        let a = self.a * other.a + self.b * other.c;
        let b = self.a * other.b + self.b * other.d;
        let c = self.c * other.a + self.d * other.c;
        let d = self.c * other.b + self.d * other.d;
        self.a = a;
        self.b = b;
        self.c = c;
        self.d = d;
    }
    fn identity_matrix() -> LuckyClover {
        LuckyClover {
            a: 1,
            b: 0,
            c: 0,
            d: 1,
        }
    }
}

fn main() {
    let multiplier = LuckyClover {
        a: 1,
        b: 1,
        c: 1,
        d: 0,
    };
    let cubed = {
        let mut i = LuckyClover::identity_matrix();
        i.multiply(&multiplier);
        i.multiply(&multiplier);
        i.multiply(&multiplier);
        std::mem::drop(multiplier);
        i
    };
    let mut sum = 0;
    let mut fibmatrix = LuckyClover::identity_matrix();
    while fibmatrix.b <= 4_000_000 {
        sum += fibmatrix.b;
        fibmatrix.multiply(&cubed);
    }
    println!("{}", sum);
    assert_eq!(sum, 4613732)
}

• Binary Exponentiation - CP-Algorithms

package main

import "fmt"

type Matrix struct {
	a, b, c, d uint64
}

func (m *Matrix) multiply(o Matrix) {
	m.a, m.b, m.c, m.d =
		m.a*o.a+m.b*o.c,
		m.a*o.b+m.b*o.d,
		m.c*o.a+m.d*o.c,
		m.c*o.b+m.d*o.d
}

func identityMatrix() Matrix {
	return Matrix{a: 1, b: 0, c: 0, d: 1}
}

func cube() Matrix {
	i := identityMatrix()
	fib := Matrix{a: 1, b: 1, c: 1, d: 0}
	i.multiply(fib)
	i.multiply(fib)
	i.multiply(fib)
	return i
}

func Example() {
	i := identityMatrix()
	c := cube()
	sum := uint64(0)
	for i.b <= 4_000_000 {
		sum += i.b
		i.multiply(c)
	}
	fmt.Println(sum)
	// Output: 4613732
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg)
  }
}

class Matrix {
  a: number;
  b: number;
  c: number;
  d: number;
  constructor() {
    this.a = 1;
    this.b = 0;
    this.c = 0;
    this.d = 1;
  }
  multiplyLiteral(o: { a: number; b: number; c: number; d: number }) {
    const a = this.a * o.a + this.b * o.c;
    const b = this.a * o.b + this.b * o.d;
    const c = this.c * o.a + this.d * o.c;
    const d = this.c * o.b + this.d * o.d;
    this.a = a;
    this.b = b;
    this.c = c;
    this.d = d;
  }
  multiplyMatrix(o: Matrix) {
    this.multiplyLiteral(o);
  }
}

function cube(): Matrix {
  let i = new Matrix();
  const fib = { a: 1, b: 1, c: 1, d: 0 };
  i.multiplyLiteral(fib);
  i.multiplyLiteral(fib);
  i.multiplyLiteral(fib);
  return i;
}

let i = new Matrix();
const c = cube();
let sum = 0;
while (i.b <= 4_000_000) {
  sum += i.b;
  i.multiplyMatrix(c);
} 
console.log(sum);
assert(sum === 4613732);

• pow mod - e26.md

fn divide_fully(n: &mut u64, d: u64, side: &mut u64) {
    if *n % d != 0 {
        return;
    }
    while {
        *n /= d;
        *n % d == 0
    } {}
    *side = (*n as f64).sqrt() as u64;
}

fn largest_prime_factor(mut n: u64) -> u64 {
    assert!(n > 1);
    let mut side = (n as f64).sqrt() as u64;
    let basic_primes = [2u64, 3, 5];
    for &d in &basic_primes {
        divide_fully(&mut n, d, &mut side);
        if n == 1 {
            return d;
        }
    }
    let mut divisor = 5u64;
    for i in [2u64, 4].iter().cycle() {
        divisor += *i;
        if divisor > side {
            break;
        }
        divide_fully(&mut n, divisor, &mut side);
        if n == 1 {
            return divisor;
        }
    }
    n
}

fn main() {
    let ans = largest_prime_factor(600851475143u64);
    assert_eq!(ans, 6857);
    println!("{}", ans);
    assert_eq!(largest_prime_factor(60), 5);
    assert_eq!(largest_prime_factor(5), 5);
    assert_eq!(largest_prime_factor(17), 17);
    assert_eq!(largest_prime_factor(6), 3);
    assert_eq!(largest_prime_factor(15), 5);
    assert_eq!(largest_prime_factor(25698751364526), 328513);
    assert_eq!(largest_prime_factor(13195), 29);
}

fn largest_prime_factor(mut n: u64) -> u64 {
    assert!(n > 1);
    let mut divisor = 2u64;
    while n != 1 {
        if n % divisor == 0 {
            n /= divisor;
        } else {
            divisor += 1;
        }
    }
    divisor
}

fn main() {
    let ans = largest_prime_factor(600851475143u64);
    assert_eq!(ans, 6857);
    println!("{}", ans);
    assert_eq!(largest_prime_factor(60), 5);
    assert_eq!(largest_prime_factor(5), 5);
    assert_eq!(largest_prime_factor(17), 17);
    assert_eq!(largest_prime_factor(6), 3);
    assert_eq!(largest_prime_factor(15), 5);
    assert_eq!(largest_prime_factor(25698751364526), 328513);
    assert_eq!(largest_prime_factor(13195), 29);
}

package main

import (
	"fmt"
	"log"
	"math"
)

func divideFully(n *uint64, d uint64, side *uint64) {
	if *n%d != 0 {
		return
	}
	for ok := true; ok; ok = *n%d == 0 {
		*n /= d
	}
	*side = uint64(math.Sqrt(float64(*n)))
}

type Divisor struct {
	d uint64
	f uint8
}

func (d *Divisor) increment() {
	d.d += uint64(2) << d.f
	d.f ^= 1
}

func largestPrimeFactor(n uint64) uint64 {
	if n < 2 {
		log.Fatal("n must be > 1.")
	}
	side := uint64(math.Sqrt(float64(n)))
	for _, d := range []uint64{2, 3, 5} {
		divideFully(&n, d, &side)
		if n == 1 {
			return d
		}
	}
	d := Divisor{d: 5}
	for {
		d.increment()
		if d.d > side {
			break
		}
		divideFully(&n, d.d, &side)
		if n == 1 {
			return d.d
		}
	}
	return n
}

func Example() {
	ans := largestPrimeFactor(600851475143)
	fmt.Println(ans)
	// Output: 6857
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

class Divisor {
  d: number;
  #f: number;
  constructor() {
    this.d = 5;
    this.#f = 0;
  }
  increment() {
    this.d += 2 << this.#f;
    this.#f ^= 1;
  }
}

function divideFully(n: number, d: number, side: number): [number, number] {
  if (n % d != 0) {
    return [n, side];
  }
  do {
    n /= d | 0;
  } while (n % d === 0);
  return [n, Math.sqrt(n) | 0];
}

function largestPrimeFactor(n: number): number {
  assert(Number.isInteger(n));
  assert(n > 1);
  let side = Math.sqrt(n) | 0;
  for (const d of [2, 3, 5]) {
    [n, side] = divideFully(n, d, side);
    if (n === 1) {
      return d;
    }
  }
  const d = new Divisor();
  while (true) {
    d.increment();
    if (d.d > side) {
      break;
    }
    [n, side] = divideFully(n, d.d, side);
    if (n === 1) {
      return d.d;
    }
  }
  return n;
}

let ans = largestPrimeFactor(600851475143);
console.log(ans);
assert(ans === 6857);

fn is_palindrome(a: u32) -> bool {
    let mut t = a;
    let mut b = 0u32;
    while t > 0 {
        b *= 10;
        b += t % 10;
        t /= 10;
    }
    a == b
}

fn update_largest_palindrome_product(lpp: &mut Option<u32>, with: u32) {
    match lpp.as_mut() {
        Some(v) => *v = with,
        None => *lpp = Some(with),
    }
}

fn scan_b(a: u32, largest_pp: &mut Option<u32>) {
    for b in (a..=999).rev() {
        let p = a * b;
        if p <= largest_pp.unwrap_or_default() {
            return;
        }
        if is_palindrome(p) {
            update_largest_palindrome_product(largest_pp, p);
        }
    }
}

fn main() {
    let mut largest_pal_pro: Option<u32> = None;
    for a in (110..=990).rev().step_by(11) {
        scan_b(a, &mut largest_pal_pro);
    }
    let ans = largest_pal_pro.unwrap();

    println!("{}", ans);
    assert_eq!(ans, 906609);
}

package main

import "fmt"

func isPalindrome(p int) bool {
	t := int(p)
	q := 0
	for t > 0 {
		q = q*10 + t%10
		t /= 10
	}
	return p == q
}

func scanB(a, lpp int) int {
	for b := 999; b >= a; b-- {
		p := a * b
		if p <= lpp {
			return lpp
		}
		if !isPalindrome(p) {
			continue
		}
		if p > lpp {
			lpp = p
		}
	}
	return lpp
}

func Example() {
	lpp := 0
	for a := 990; a >= 110; a -= 11 {
		lpp = scanB(a, lpp)
	}
	fmt.Println(lpp)
	// Output: 906609
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

function isPalindrome(p: number): boolean {
  let t = Number(p);
  let q = 0;
  while (t > 0) {
    q = q * 10 + t % 10;
    t = t / 10 | 0;
  }
  return p === q;
}

function scanB(a: number, lpp: number): number {
  for (let b = 999; b >= a; b--) {
    const p = a * b;
    if (p <= lpp) {
      return lpp;
    }
    if (isPalindrome(p)) {
      lpp = Math.max(lpp, p);
    }
  }
  return lpp;
}

let lpp = 0;
for (let a = 990; a >= 110; a -= 11) {
  lpp = scanB(a, lpp);
}
console.log(lpp);
assert(lpp === 906609);

• https://en.wikipedia.org/wiki/Divisibility_rule#Divisibility_by_7

fn gcd(mut a: u64, mut b: u64) -> u64 {
    assert!(a != 0 && b != 0);
    while b != 0 {
        let r = a % b;
        a = b;
        b = r;
    }
    a
}

fn lcm(a: u64, b: u64) -> u64 {
    a * b / gcd(a, b)
}

fn main() {
    let mut acc = 2u64;
    for n in 3..=20u64 {
        acc = lcm(acc, n);
    }

    println!("{}", acc);
    assert_eq!(acc, 232792560);
}

#[derive(Clone)]
struct Factor {
    prime: u32,
    occurrence: u32,
}

fn increment_occurrence(factors: &mut [Option<Factor>; 20], p: u32) {
    if let Some(f) = factors[p as usize].as_mut() {
        f.occurrence += 1;
        return;
    }
    factors[p as usize] = Some(Factor {
        prime: p,
        occurrence: 1,
    });
}

fn list_factors(mut n: u32) -> [Option<Factor>; 20] {
    assert!(n <= 20);
    let mut factors: [Option<Factor>; 20] = Default::default();
    let mut d = 2u32;
    while n > 1 {
        while n % d == 0 {
            increment_occurrence(&mut factors, d);
            n /= d;
        }
        d += 1;
    }
    factors
}

fn merge(factors: &mut [Option<Factor>; 20], b: &[Option<Factor>; 20]) {
    for it in b.iter().zip(factors.iter_mut()) {
        match it {
            (Some(bf), None) => *it.1 = Some(bf.clone()),
            (Some(bf), Some(f)) if bf.occurrence > f.occurrence => {
                f.occurrence = bf.occurrence
            },
            _ => continue,
        }
    }
}

fn main() {
    let mut factors: [Option<Factor>; 20] = Default::default();
    for n in 2..=20u32 {
        let local_factors = list_factors(n);
        merge(&mut factors, &local_factors);
    }
    let mut acc = 1u32;
    for o in &factors {
        if let Some(f) = o {
            acc *= f.prime.pow(f.occurrence);
        }
    }

    println!("{}", acc);
    assert_eq!(acc, 232792560);
}

package main

import (
	"fmt"
	"log"
)

func gcd(a, b uint64) uint64 {
	if a == 0 || b == 0 {
		log.Fatal("gcd(0) is undefined.")
	}
	for b != 0 {
		a, b = b, a%b
	}
	return a
}

func lcm(a, b uint64) uint64 {
	return a * b / gcd(a, b)
}

func Example() {
	acc := uint64(2)
	for n := uint64(3); n <= 20; n++ {
		acc = lcm(acc, n)
	}
	fmt.Println(acc)
	// Output: 232792560
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

function gcd(a: number, b: number): number {
  assert(Number.isInteger(a) && Number.isInteger(b));
  assert(Math.sign(a) === 1 && Math.sign(b) === 1);
  let t: number;
  while (b != 0) {
    t = Number(a);
    a = b;
    b = t % b;
  }
  return a;
}

function lcm(a: number, b: number): number {
  return a * b / gcd(a, b);
}

let acc = 2;
for (let n = 3; n <= 20; n++) {
  acc = lcm(acc, n);
}
console.log(acc);
assert(acc === 232792560);

struct Sequence {
    n: u64,
}

impl Sequence {
    fn sum_of_squares(&self) -> u64 {
        self.n * (self.n + 1) * (2 * self.n + 1) / 6
    }
    fn sum(&self) -> u64 {
        (1 + self.n) * self.n / 2
    }
}

fn main() {
    let s = Sequence{n: 100};
    let sum = s.sum();
    let diff = sum * sum - s.sum_of_squares();

    println!("{}", diff);
    assert_eq!(diff, 25164150);
}

package main

import "fmt"

type Sequence struct {
	n uint64
}

func (s *Sequence) sumOfSquares() uint64 {
	return s.n * (s.n + 1) * (2*s.n + 1) / 6
}

func (s *Sequence) sum() uint64 {
	return (1 + s.n) * s.n / 2
}

func Example() {
	s := Sequence{n: 100}
	sum := s.sum()
	diff := sum*sum - s.sumOfSquares()
	fmt.Println(diff)
	// Output: 25164150
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

interface Sequence {
  n: number;
}

function sumOfSquares(s: Sequence): number {
  return s.n * (s.n + 1) * (2 * s.n + 1) / 6;
}

function sum(s: Sequence): number {
  return (1 + s.n) * s.n / 2;
}

const s: Sequence = { n: 100 };
const su = sum(s);
const diff = su * su - sumOfSquares(s);
console.log(diff);
assert(diff === 25164150);

• Sieve of Eratosthenes, number square, view multiples and prime numbers - visnos.com

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn rule_out_from_previous_position(sieve: &mut Vec<bool>, prime: usize, pp: usize) {
    use std::cmp::max;
    let begin = max((((pp - 1) / prime) + 1) * prime, prime * prime);
    for i in (begin..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn extend(sieve: &mut Vec<bool>, primes: &Vec<usize>) {
    let previous_len = sieve.len();
    sieve.extend(vec![true; previous_len]);
    for &p in primes {
        rule_out_from_previous_position(sieve, p, previous_len);
    }
}

fn main() {
    let mut counter = 2u32;
    let mut sieve = vec![true; 10000];
    let mut primes: Vec<usize> = vec![];
    let mut cursor = 5usize;
    let mut ite = [2usize, 4].iter().cycle();
    let n = 'exploration: loop {
        while cursor < sieve.len() {
            if !sieve[cursor] {
                cursor += ite.next().unwrap();
                continue;
            }
            counter += 1;
            if counter == 10001 {
                break 'exploration cursor as u64;
            }
            &primes.push(cursor);
            rule_out(&mut sieve, cursor);
            cursor += ite.next().unwrap();
        }
        extend(&mut sieve, &primes);
    };

    println!("{}", n);
    assert_eq!(n, 104743);
}

fn is_prime(n: u64) -> bool {
    if n < 2 {
        return false;
    }
    if n == 2 || n == 3 || n == 5 {
        return true;
    }
    for d in &[2u64, 3, 5] {
        if n % *d == 0 {
            return false;
        }
    }
    let side = (n as f64).sqrt() as u64;
    let mut d = 5u64;
    for i in [2u64, 4].iter().cycle() {
        d += *i;
        if d > side {
            break;
        }
        if n % d == 0 {
            return false;
        }
    }
    true
}

fn main() {
    let mut n = 0u64;
    let mut counter = 0u32;
    while counter < 10001 {
        n += 1;
        if is_prime(n) {
            counter += 1;
        }
    }
    
    println!("{}", n);
    assert_eq!(n, 104743);
}

• Q.3 Largest prime factor

package main

import "fmt"

type Index struct {
	i int
	f uint8
}

func (i *Index) increment() {
	i.i += 2 << i.f
	i.f ^= 1
}

func ruleout(sieve []bool, p int) {
	for i := p * p; i < len(sieve); i += p {
		sieve[i] = true
	}
}

func ruleoutFromPosition(sieve []bool, prime, position int) {
	pos := (((position - 1) / prime) + 1) * prime
	sq := prime * prime
	if pos < sq {
		pos = sq
	}
	for i := pos; i < len(sieve); i += prime {
		sieve[i] = true
	}
}

func extend(sieve *[]bool, primes []int) {
	previousLen := len(*sieve)
	*sieve = append(*sieve, make([]bool, previousLen)...)
	for _, p := range primes {
		ruleoutFromPosition(*sieve, p, previousLen)
	}
}

func Example() {
	counter := 2
	sieve := make([]bool, 10000)
	primes := []int{}
	i := Index{i: 5}
Exploration:
	for {
		for i.i < len(sieve) {
			if sieve[i.i] {
				i.increment()
				continue
			}
			counter++
			if counter == 10001 {
				break Exploration
			}
			primes = append(primes, i.i)
			ruleout(sieve, i.i)
			i.increment()
		}
		extend(&sieve, primes)
	}
	fmt.Println(i.i)
	// Output: 104743
}

https://stackoverflow.com/questions/23304854/how-do-you-determine-if-a-variable-is-a-slice-or-array

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

class Index {
  i: number;
  #f: number;
  constructor() {
    this.i = 5;
    this.#f = 0;
  }
  increment() {
    this.i += 2 << this.#f;
    this.#f ^= 1;
  }
}

function ruleoutFromPosition(
  sieve: boolean[],
  prime: number,
  position: number,
) {
  const sq = prime * prime;
  const head = (((position - 1) / prime | 0) + 1) * prime;
  for (let i = Math.max(sq, head); i < sieve.length; i += prime) {
    sieve[i] = false;
  }
}

function ruleout(sieve: boolean[], p: number) {
  for (let i = p * p; i < sieve.length; i += p) {
    sieve[i] = false;
  }
}

function extend(sieve: boolean[], primes: number[]) {
  const previousLen = sieve.length;
  sieve.push(...Array(previousLen).fill(true));
  for (const p of primes) {
    ruleoutFromPosition(sieve, p, previousLen);
  }
}

let counter = 2;
let sieve = Array(10000).fill(true);
let primes = [];
const i = new Index();
exploration:
while (true) {
  while (i.i < sieve.length) {
    if (!sieve[i.i]) {
      i.increment();
      continue;
    }
    counter++;
    if (counter === 10001) {
      break exploration;
    }
    primes.push(i.i);
    ruleout(sieve, i.i);
    i.increment();
  }
  extend(sieve, primes);
}
console.log(i.i);
assert(i.i === 104743);

• https://en.wikipedia.org/wiki/Logical_connective#Overview
• https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Bitwise_XOR

• https://www.khanacademy.org/computing/computer-science/cryptography

fn main() {
    let thousand_digits = "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450";
    let zero = '0' as u8;
    let digits = thousand_digits
        .chars()
        .map(|c| c as u8 - zero)
        .collect::<Vec<u8>>();
    let mut max = 0u64;
    for i in 0..digits.len() - 13 {
        let tmp = digits[i..i + 13].iter().map(|&d| d as u64).product();
        max = std::cmp::max(max, tmp);
    }

    println!("{}", max);
    assert_eq!(max, 23514624000);
}

fn main() {
    let thousand_digits = "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450";
    let zero = '0' as u8;
    let digits = thousand_digits
        .chars()
        .map(|c| c as u8 - zero)
        .collect::<Vec<u8>>();
    let mut product = digits[0..=12].iter().map(|&d| d as u64).product::<u64>();
    let mut max = product.clone();
    for i in 13..digits.len() {
        let outgoing = digits[i - 13];
        if outgoing == 0 {
            product = digits[i - 12..=i].iter().map(|&d| d as u64).product();
        } else {
            product /= outgoing as u64;
            product *= digits[i] as u64;
        }
        max = std::cmp::max(max, product);
    }

    println!("{}", max);
    assert_eq!(max, 23514624000);
}

With go and javascript, the memorization made it faster.

package main

import "fmt"

// 22810 ns/op
func ExampleA() {
	thousandDigits := "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450"
	zero := int('0')
	runes := []rune(thousandDigits)
	digits := make([]int, len(runes))
	for i, r := range runes {
		digits[i] = int(r) - zero
	}
	max := 0
	for i := 0; i < len(digits)-13; i++ {
		product := digits[i]
		for _, v := range digits[i+1 : i+13] {
			product *= v
		}
		if max < product {
			max = product
		}
	}
	fmt.Println(max)
	// Output: 23514624000
}

// 10994 ns/op
func ExampleB() {
	thousandDigits := "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450"
	zero := int('0')
	runes := []rune(thousandDigits)
	digits := make([]int, len(runes))
	for i, r := range runes {
		digits[i] = int(r) - zero
	}
	product := 1
	for _, v := range digits[0:13] {
		product *= v
	}
	max := int(product)
	for i := 13; i < len(digits); i++ {
		outgoing := digits[i-13]
		if outgoing == 0 {
			product = digits[i]
			for _, v := range digits[i-12 : i] {
				product *= v
			}
		} else {
			product /= outgoing
			product *= digits[i]
		}
		if max < product {
			max = product
		}
	}
	fmt.Println(max)
	// Output: 23514624000
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

// 118 us
function a() {
  const thousandDigits =
    "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450";
  const zero = "0".charCodeAt(0);
  const chars = Array.from(thousandDigits);
  const digits = chars.map((c) => c.charCodeAt(0) - zero);
  let max = 0;
  for (let i = 0; i < digits.length - 13; i++) {
    const product = digits.slice(i, i + 13).reduce((acc, v) => acc * v);
    max = Math.max(max, product);
  }
  console.log(max);
  assert(max === 23514624000);
}

// 52 us
function b() {
  const thousandDigits =
    "7316717653133062491922511967442657474235534919493496983520312774506326239578318016984801869478851843858615607891129494954595017379583319528532088055111254069874715852386305071569329096329522744304355766896648950445244523161731856403098711121722383113622298934233803081353362766142828064444866452387493035890729629049156044077239071381051585930796086670172427121883998797908792274921901699720888093776657273330010533678812202354218097512545405947522435258490771167055601360483958644670632441572215539753697817977846174064955149290862569321978468622482839722413756570560574902614079729686524145351004748216637048440319989000889524345065854122758866688116427171479924442928230863465674813919123162824586178664583591245665294765456828489128831426076900422421902267105562632111110937054421750694165896040807198403850962455444362981230987879927244284909188845801561660979191338754992005240636899125607176060588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450";
  const zero = "0".charCodeAt(0);
  const chars = Array.from(thousandDigits);
  const digits = chars.map((c) => c.charCodeAt(0) - zero);
  let product = digits.slice(0, 13).reduce((acc, v) => acc * v);
  let max = Number(product);
  for (let i = 13; i < digits.length; i++) {
    const outgoing = digits[i - 13];
    if (outgoing == 0) {
      product = digits.slice(i - 12, i + 1).reduce((acc, v) => acc * v);
    } else {
      product /= outgoing;
      product *= digits[i];
    }
    max = Math.max(max, product);
  }
  console.log(max);
  assert(max === 23514624000);
}

a();
b();

• Q.39 Integer right triangles

fn main() {
    let mut ans = None;
    'exploration: for m in 2..=(499f32.sqrt() as u32) {
        for n in 1..m {
            let a = m * m - n * n;
            let b = 2 * m * n;
            let c = m * m + n * n;
            if a + b + c == 1000 {
                ans = Some(a * b * c);
                break 'exploration;
            }
        }
    }

    println!("{:?}", ans);
    assert_eq!(ans.unwrap(), 31875000);
}

package main

import (
	"fmt"
	"math"
	"testing"
)

func Example() {
	var ans uint32
Exploration:
	for m := uint32(2); m <= uint32(math.Sqrt(float64(499))); m++ {
		for n := uint32(1); n < m; n++ {
			a := m*m - n*n
			b := 2 * m * n
			c := m*m + n*n
			if a+b+c == 1000 {
				ans = a * b * c
				break Exploration
			}
		}
	}
	fmt.Println(ans)
	// Output: 31875000
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

let ans = 0;
exploration:
for (let m = 2; m <= (Math.sqrt(499) | 0); m++) {
  for (let n = 1; n < m; n++) {
    const a = m * m - n * n;
    const b = 2 * m * n;
    const c = m * m + n * n;
    if (a + b + c === 1000) {
      ans = a * b * c;
      break exploration;
    }
  }
}
console.log(ans);
assert(ans === 31875000);

• Q.7 10001st prime

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut [bool; 2_000_001], prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn main() {
    let mut sieve = [true; 2_000_001];
    let sqrt = ((sieve.len() - 1) as f64).sqrt() as usize;
    let mut sum = 2u64 + 3;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            sum += index.i as u64;
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            sum += index.i as u64;
        }
        index.increment();
    }

    println!("{}", sum);
    assert_eq!(sum, 142913828922);
}

mod index {
    pub struct Index {
        pub i: usize,
        ite: Box<dyn Iterator<Item = usize>>,
    }
    impl Index {
        pub fn increment(&mut self) {
            self.i += self.ite.next().unwrap();
        }
        pub fn new() -> Self {
            Self {
                i: 5,
                ite: Box::new(vec![2usize, 4].into_iter().cycle()),
            }
        }
    }
}

fn rule_out(sieve: &mut [bool; 2_000_001], prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn main() {
    let mut sieve = [true; 2_000_001];
    let sqrt = ((sieve.len() - 1) as f64).sqrt() as usize;
    let mut sum = 2u64 + 3;
    let mut index = index::Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            sum += index.i as u64;
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            sum += index.i as u64;
        }
        index.increment();
    }

    println!("{}", sum);
    assert_eq!(sum, 142913828922);
}

package main

import (
	"fmt"
	"math"
	"testing"
)

type Index struct {
	i int
	f uint8
}

func (i *Index) increment() {
	i.i += 2 << i.f
	i.f ^= 1
}

func ruleout(sieve []bool, p int) {
	for i := p * p; i < len(sieve); i += p {
		sieve[i] = true
	}
}

func Example() {
	n := 2_000_000
	sieve := make([]bool, n+1)
	side := int(math.Sqrt(float64(n)))
	i := Index{i: 5}
	sum := 2 + 3
	for i.i <= side {
		if !sieve[i.i] {
			ruleout(sieve, i.i)
			sum += i.i
		}
		i.increment()
	}
	for i.i < len(sieve) {
		if !sieve[i.i] {
			sum += i.i
		}
		i.increment()
	}

	fmt.Println(sum)
	// Output: 142913828922
}

function assert(condition: any, msg?: string): asserts condition {
  if (!condition) {
    throw new Error(msg);
  }
}

class Index {
  i: number;
  #f: number;
  constructor() {
    this.i = 5;
    this.#f = 0;
  }
  increment() {
    this.i += 2 << this.#f;
    this.#f ^= 1;
  }
}

function ruleout(sieve: boolean[], p: number) {
  for (let i = p * p; i < sieve.length; i += p) {
    sieve[i] = false;
  }
}

const n = 2_000_000;
let sieve = Array(n + 1).fill(true);
const side = Math.sqrt(n) | 0;
let sum = 2 + 3;
const i = new Index();
while (i.i <= side) {
  if (sieve[i.i]) {
    sum += i.i;
    ruleout(sieve, i.i);
  }
  i.increment();
}
while (i.i < sieve.length) {
  if (sieve[i.i]) {
    sum += i.i;
  }
  i.increment();
}
console.log(sum);
assert(sum === 142913828922);

fn main() {
    let matrix = MATRIX;
    let mut max = 0u32;

    // →
    for y in matrix {
        for x in 3..matrix.len() {
            if let (Some(a), Some(b), Some(c), Some(d)) =
                (y.get(x - 3), y.get(x - 2), y.get(x - 1), y.get(x))
            {
                max = std::cmp::max(max, a * b * c * d);
            }
        }
    }

    // ↓
    for x in 0..matrix.len() {
        for y in 3..matrix.len() {
            if let (Some(a), Some(b), Some(c), Some(d)) = (
                matrix.get(y - 3).and_then(|r| r.get(x)),
                matrix.get(y - 2).and_then(|r| r.get(x)),
                matrix.get(y - 1).and_then(|r| r.get(x)),
                matrix.get(y).and_then(|r| r.get(x)),
            ) {
                max = std::cmp::max(max, a * b * c * d);
            }
        }
    }

    // ↘
    for x in 3..matrix.len() {
        for y in 3..matrix.len() {
            if let (Some(a), Some(b), Some(c), Some(d)) = (
                matrix.get(y - 3).and_then(|r| r.get(x - 3)),
                matrix.get(y - 2).and_then(|r| r.get(x - 2)),
                matrix.get(y - 1).and_then(|r| r.get(x - 1)),
                matrix.get(y).and_then(|r| r.get(x)),
            ) {
                max = std::cmp::max(max, a * b * c * d);
            }
        }
    }

    // ↙
    for x in 3..matrix.len() {
        for y in 0..matrix.len() - 3 {
            if let (Some(a), Some(b), Some(c), Some(d)) = (
                matrix.get(y + 3).and_then(|r| r.get(x - 3)),
                matrix.get(y + 2).and_then(|r| r.get(x - 2)),
                matrix.get(y + 1).and_then(|r| r.get(x - 1)),
                matrix.get(y).and_then(|r| r.get(x)),
            ) {
                max = std::cmp::max(max, a * b * c * d);
            }
        }
    }

    println!("{}", max);
    assert_eq!(max, 70600674);
}

const MATRIX: [[u32; 20]; 20] = [
    [08, 02, 22, 97, 38, 15, 00, 40, 00, 75, 04, 05, 07, 78, 52, 12, 50, 77, 91, 08,],
    [49, 49, 99, 40, 17, 81, 18, 57, 60, 87, 17, 40, 98, 43, 69, 48, 04, 56, 62, 00,],
    [81, 49, 31, 73, 55, 79, 14, 29, 93, 71, 40, 67, 53, 88, 30, 03, 49, 13, 36, 65,],
    [52, 70, 95, 23, 04, 60, 11, 42, 69, 24, 68, 56, 01, 32, 56, 71, 37, 02, 36, 91,],
    [22, 31, 16, 71, 51, 67, 63, 89, 41, 92, 36, 54, 22, 40, 40, 28, 66, 33, 13, 80,],
    [24, 47, 32, 60, 99, 03, 45, 02, 44, 75, 33, 53, 78, 36, 84, 20, 35, 17, 12, 50,],
    [32, 98, 81, 28, 64, 23, 67, 10, 26, 38, 40, 67, 59, 54, 70, 66, 18, 38, 64, 70,],
    [67, 26, 20, 68, 02, 62, 12, 20, 95, 63, 94, 39, 63, 08, 40, 91, 66, 49, 94, 21,],
    [24, 55, 58, 05, 66, 73, 99, 26, 97, 17, 78, 78, 96, 83, 14, 88, 34, 89, 63, 72,],
    [21, 36, 23, 09, 75, 00, 76, 44, 20, 45, 35, 14, 00, 61, 33, 97, 34, 31, 33, 95,],
    [78, 17, 53, 28, 22, 75, 31, 67, 15, 94, 03, 80, 04, 62, 16, 14, 09, 53, 56, 92,],
    [16, 39, 05, 42, 96, 35, 31, 47, 55, 58, 88, 24, 00, 17, 54, 24, 36, 29, 85, 57,],
    [86, 56, 00, 48, 35, 71, 89, 07, 05, 44, 44, 37, 44, 60, 21, 58, 51, 54, 17, 58,],
    [19, 80, 81, 68, 05, 94, 47, 69, 28, 73, 92, 13, 86, 52, 17, 77, 04, 89, 55, 40,],
    [04, 52, 08, 83, 97, 35, 99, 16, 07, 97, 57, 32, 16, 26, 26, 79, 33, 27, 98, 66,],
    [88, 36, 68, 87, 57, 62, 20, 72, 03, 46, 33, 67, 46, 55, 12, 32, 63, 93, 53, 69,],
    [04, 42, 16, 73, 38, 25, 39, 11, 24, 94, 72, 18, 08, 46, 29, 32, 40, 62, 76, 36,],
    [20, 69, 36, 41, 72, 30, 23, 88, 34, 62, 99, 69, 82, 67, 59, 85, 74, 04, 36, 16,],
    [20, 73, 35, 29, 78, 31, 90, 01, 74, 31, 49, 71, 48, 86, 81, 16, 23, 57, 05, 54,],
    [01, 70, 54, 71, 83, 51, 54, 69, 16, 92, 33, 48, 61, 43, 52, 01, 89, 19, 67, 48,],
];

struct Square {
    _matrix: [[u32; 20]; 20],
    _x: usize,
    _y: usize,
    _width: usize,
}

impl Square {
    fn new(matrix: [[u32; 20]; 20]) -> Self {
        assert!(matrix.len() == 0 || matrix.len() == matrix[0].len());
        Self {
            _x: 0,
            _y: 0,
            _matrix: matrix,
            _width: matrix.len(),
        }
    }
    fn width(&self) -> usize {
        self._width
    }
    fn set_cursor(&mut self, x: usize, y: usize) {
        self._x = x;
        self._y = y;
    }
    fn east_product(&self, adj_len: usize) -> Result<u32, ()> {
        if self._x + adj_len > self._matrix.len() {
            return Err(());
        }
        let p = (0..adj_len)
            .map(|a| self._matrix[self._y][self._x + a])
            .product::<u32>();
        Ok(p)
    }
    fn south_product(&self, adj_len: usize) -> Result<u32, ()> {
        if self._y + adj_len > self._matrix.len() {
            return Err(());
        }
        let p = (0..adj_len)
            .map(|a| self._matrix[self._y + a][self._x])
            .product::<u32>();
        Ok(p)
    }
    fn south_east_product(&self, adj_len: usize) -> Result<u32, ()> {
        if self._y + adj_len > self._matrix.len() {
            return Err(());
        }
        if self._x + adj_len > self._matrix.len() {
            return Err(());
        }
        let p = (0..adj_len)
            .map(|a| self._matrix[self._y + a][self._x + a])
            .product::<u32>();
        Ok(p)
    }
    fn south_west_product(&self, adj_len: usize) -> Result<u32, ()> {
        if self._y + adj_len > self._matrix.len() {
            return Err(());
        }
        if self._x < adj_len - 1 {
            return Err(());
        }
        let p = (0..adj_len)
            .map(|a| self._matrix[self._y + a][self._x - a])
            .product::<u32>();
        Ok(p)
    }
}

fn main() {
    let mut square = Square::new(MATRIX);

    let mut max = 0u32;
    for i in 0..square.width() {
        for j in 0..square.width() {
            square.set_cursor(i, j);
            if let Ok(p) = square.east_product(4) {
                max = std::cmp::max(max, p);
            }
            if let Ok(p) = square.south_product(4) {
                max = std::cmp::max(max, p);
            }
            if let Ok(p) = square.south_east_product(4) {
                max = std::cmp::max(max, p);
            }
            if let Ok(p) = square.south_west_product(4) {
                max = std::cmp::max(max, p);
            }
        }
    }

    println!("{}", max);
    assert_eq!(max, 70600674);
}


const MATRIX: [[u32; 20]; 20] = [
    [08, 02, 22, 97, 38, 15, 00, 40, 00, 75, 04, 05, 07, 78, 52, 12, 50, 77, 91, 08,],
    [49, 49, 99, 40, 17, 81, 18, 57, 60, 87, 17, 40, 98, 43, 69, 48, 04, 56, 62, 00,],
    [81, 49, 31, 73, 55, 79, 14, 29, 93, 71, 40, 67, 53, 88, 30, 03, 49, 13, 36, 65,],
    [52, 70, 95, 23, 04, 60, 11, 42, 69, 24, 68, 56, 01, 32, 56, 71, 37, 02, 36, 91,],
    [22, 31, 16, 71, 51, 67, 63, 89, 41, 92, 36, 54, 22, 40, 40, 28, 66, 33, 13, 80,],
    [24, 47, 32, 60, 99, 03, 45, 02, 44, 75, 33, 53, 78, 36, 84, 20, 35, 17, 12, 50,],
    [32, 98, 81, 28, 64, 23, 67, 10, 26, 38, 40, 67, 59, 54, 70, 66, 18, 38, 64, 70,],
    [67, 26, 20, 68, 02, 62, 12, 20, 95, 63, 94, 39, 63, 08, 40, 91, 66, 49, 94, 21,],
    [24, 55, 58, 05, 66, 73, 99, 26, 97, 17, 78, 78, 96, 83, 14, 88, 34, 89, 63, 72,],
    [21, 36, 23, 09, 75, 00, 76, 44, 20, 45, 35, 14, 00, 61, 33, 97, 34, 31, 33, 95,],
    [78, 17, 53, 28, 22, 75, 31, 67, 15, 94, 03, 80, 04, 62, 16, 14, 09, 53, 56, 92,],
    [16, 39, 05, 42, 96, 35, 31, 47, 55, 58, 88, 24, 00, 17, 54, 24, 36, 29, 85, 57,],
    [86, 56, 00, 48, 35, 71, 89, 07, 05, 44, 44, 37, 44, 60, 21, 58, 51, 54, 17, 58,],
    [19, 80, 81, 68, 05, 94, 47, 69, 28, 73, 92, 13, 86, 52, 17, 77, 04, 89, 55, 40,],
    [04, 52, 08, 83, 97, 35, 99, 16, 07, 97, 57, 32, 16, 26, 26, 79, 33, 27, 98, 66,],
    [88, 36, 68, 87, 57, 62, 20, 72, 03, 46, 33, 67, 46, 55, 12, 32, 63, 93, 53, 69,],
    [04, 42, 16, 73, 38, 25, 39, 11, 24, 94, 72, 18, 08, 46, 29, 32, 40, 62, 76, 36,],
    [20, 69, 36, 41, 72, 30, 23, 88, 34, 62, 99, 69, 82, 67, 59, 85, 74, 04, 36, 16,],
    [20, 73, 35, 29, 78, 31, 90, 01, 74, 31, 49, 71, 48, 86, 81, 16, 23, 57, 05, 54,],
    [01, 70, 54, 71, 83, 51, 54, 69, 16, 92, 33, 48, 61, 43, 52, 01, 89, 19, 67, 48,],
];

They both store data in a linear contiguous array where accessing or iterating is both an O(1) operation so there's no difference in performance.

Performance of Rust vector (Vec<T>) versus array ([T; n]) [closed]

• Q.3 Largest prime factor

struct TriangleNumber {
    _nth: u64,
    _primes: Vec<u64>,
    _num_div_even: u64,
    _num_div_odd: u64,
}

trait Divisors {
    fn number_of_divisors(&self) -> u64;
}

impl TriangleNumber {
    fn new() -> Self {
        Self {
            _nth: 3,
            _num_div_even: 2,
            _num_div_odd: 2,
            _primes: vec![2, 3],
        }
    }
    fn num(&self) -> u64 {
        self._nth * (self._nth + 1) / 2
    }
    fn _divide_fully(&self, n: &mut u64, d: u64, side: &mut u64, count: &mut u64) {
        if *n % d != 0 {
            return;
        }
        let mut exp = 0u64;
        while {
            *n /= d;
            exp += 1;
            *n % d == 0
        } {}
        *side = (*n as f64).sqrt() as u64;
        *count *= exp + 1;
    }
    fn _num_of_divisors(&mut self, mut n: u64) -> u64 {
        let mut count = 1u64;
        let mut side = (n as f64).sqrt() as u64;
        for p in &self._primes {
            if p > side || n == 1 {
                break;
            }
            self._divide_fully(&mut n, p, &mut side, &mut count);
        }
        if n != 1 {
            count *= 2;
            self._primes.push(n);
        }
        count
    }
    fn increment(&mut self) {
        self._nth += 1;
        if self._nth % 2 == 0 {
            self._num_div_odd = self._num_of_divisors(self._nth + 1);
        } else {
            self._num_div_even = self._num_of_divisors((self._nth + 1) / 2);
        }
    }
}

impl Divisors for TriangleNumber {
    fn number_of_divisors(&self) -> u64 {
        self._num_div_even * self._num_div_odd
    }
}

fn main() {
    let mut triangle_number = TriangleNumber::new();
    while triangle_number.number_of_divisors() <= 500 {
        triangle_number.increment();
    }
    let ans = triangle_number.num();

    println!("{}", ans);
    assert_eq!(ans, 76576500);
}

• Highly_composite_number - Wikipedia

Go to 2. Variable-size input solution

1. Fixed-size input solution

fn main() {
    let input_digits = 50usize;
    let container_digits = 10usize;
    let overflow_threshold = 10u64.pow(container_digits as u32);

    let mut sum = 0u64;
    let mut carry = 0u64;
    for i in 0..input_digits / container_digits {
        let chunk_begin = input_digits - container_digits * (i + 1);
        let chunk_end = input_digits - container_digits * i;
        sum = FIFTY_DIGIT_NUMBERS
            .iter()
            .map(|&s| &s[chunk_begin..chunk_end])
            .map(|s| s.parse::<u64>().unwrap())
            .sum::<u64>()
            + carry;
        carry = sum / overflow_threshold;
    }

    let display_threshold = 10u64.pow(10);
    while sum >= display_threshold {
        sum /= 10;
    }

    println!("{}", sum);
    assert_eq!(sum, 5537376230);
}

const FIFTY_DIGIT_NUMBERS: [&str; 100] = [
    "37107287533902102798797998220837590246510135740250",
    "46376937677490009712648124896970078050417018260538",
    "74324986199524741059474233309513058123726617309629",
    "91942213363574161572522430563301811072406154908250",
    "23067588207539346171171980310421047513778063246676",
    "89261670696623633820136378418383684178734361726757",
    "28112879812849979408065481931592621691275889832738",
    "44274228917432520321923589422876796487670272189318",
    "47451445736001306439091167216856844588711603153276",
    "70386486105843025439939619828917593665686757934951",
    "62176457141856560629502157223196586755079324193331",
    "64906352462741904929101432445813822663347944758178",
    "92575867718337217661963751590579239728245598838407",
    "58203565325359399008402633568948830189458628227828",
    "80181199384826282014278194139940567587151170094390",
    "35398664372827112653829987240784473053190104293586",
    "86515506006295864861532075273371959191420517255829",
    "71693888707715466499115593487603532921714970056938",
    "54370070576826684624621495650076471787294438377604",
    "53282654108756828443191190634694037855217779295145",
    "36123272525000296071075082563815656710885258350721",
    "45876576172410976447339110607218265236877223636045",
    "17423706905851860660448207621209813287860733969412",
    "81142660418086830619328460811191061556940512689692",
    "51934325451728388641918047049293215058642563049483",
    "62467221648435076201727918039944693004732956340691",
    "15732444386908125794514089057706229429197107928209",
    "55037687525678773091862540744969844508330393682126",
    "18336384825330154686196124348767681297534375946515",
    "80386287592878490201521685554828717201219257766954",
    "78182833757993103614740356856449095527097864797581",
    "16726320100436897842553539920931837441497806860984",
    "48403098129077791799088218795327364475675590848030",
    "87086987551392711854517078544161852424320693150332",
    "59959406895756536782107074926966537676326235447210",
    "69793950679652694742597709739166693763042633987085",
    "41052684708299085211399427365734116182760315001271",
    "65378607361501080857009149939512557028198746004375",
    "35829035317434717326932123578154982629742552737307",
    "94953759765105305946966067683156574377167401875275",
    "88902802571733229619176668713819931811048770190271",
    "25267680276078003013678680992525463401061632866526",
    "36270218540497705585629946580636237993140746255962",
    "24074486908231174977792365466257246923322810917141",
    "91430288197103288597806669760892938638285025333403",
    "34413065578016127815921815005561868836468420090470",
    "23053081172816430487623791969842487255036638784583",
    "11487696932154902810424020138335124462181441773470",
    "63783299490636259666498587618221225225512486764533",
    "67720186971698544312419572409913959008952310058822",
    "95548255300263520781532296796249481641953868218774",
    "76085327132285723110424803456124867697064507995236",
    "37774242535411291684276865538926205024910326572967",
    "23701913275725675285653248258265463092207058596522",
    "29798860272258331913126375147341994889534765745501",
    "18495701454879288984856827726077713721403798879715",
    "38298203783031473527721580348144513491373226651381",
    "34829543829199918180278916522431027392251122869539",
    "40957953066405232632538044100059654939159879593635",
    "29746152185502371307642255121183693803580388584903",
    "41698116222072977186158236678424689157993532961922",
    "62467957194401269043877107275048102390895523597457",
    "23189706772547915061505504953922979530901129967519",
    "86188088225875314529584099251203829009407770775672",
    "11306739708304724483816533873502340845647058077308",
    "82959174767140363198008187129011875491310547126581",
    "97623331044818386269515456334926366572897563400500",
    "42846280183517070527831839425882145521227251250327",
    "55121603546981200581762165212827652751691296897789",
    "32238195734329339946437501907836945765883352399886",
    "75506164965184775180738168837861091527357929701337",
    "62177842752192623401942399639168044983993173312731",
    "32924185707147349566916674687634660915035914677504",
    "99518671430235219628894890102423325116913619626622",
    "73267460800591547471830798392868535206946944540724",
    "76841822524674417161514036427982273348055556214818",
    "97142617910342598647204516893989422179826088076852",
    "87783646182799346313767754307809363333018982642090",
    "10848802521674670883215120185883543223812876952786",
    "71329612474782464538636993009049310363619763878039",
    "62184073572399794223406235393808339651327408011116",
    "66627891981488087797941876876144230030984490851411",
    "60661826293682836764744779239180335110989069790714",
    "85786944089552990653640447425576083659976645795096",
    "66024396409905389607120198219976047599490197230297",
    "64913982680032973156037120041377903785566085089252",
    "16730939319872750275468906903707539413042652315011",
    "94809377245048795150954100921645863754710598436791",
    "78639167021187492431995700641917969777599028300699",
    "15368713711936614952811305876380278410754449733078",
    "40789923115535562561142322423255033685442488917353",
    "44889911501440648020369068063960672322193204149535",
    "41503128880339536053299340368006977710650566631954",
    "81234880673210146739058568557934581403627822703280",
    "82616570773948327592232845941706525094512325230608",
    "22918802058777319719839450180888072429661980811197",
    "77158542502016545090413245809786882778948721859617",
    "72107838435069186155435662884062257473692284509516",
    "20849603980134001723930671666823555245252804609722",
    "53503534226472524250874054075591789781264330331690",
];

Go to 1. Fixed-size input solution

2. Variable-size input solution

struct BigNum {
    a: Vec<u64>,
}

fn paging(b: &str, page: usize, unit: usize) -> Option<&str> {
    let len = b.len();
    if len <= unit && page == 0 {
        return Some(b);
    } else if len <= unit && page > 0 {
        return None;
    }
    let end = len as isize - page as isize * unit as isize;
    if end <= 0 {
        return None;
    }
    let begin = end - unit as isize;
    if begin < 0 {
        Some(&b[0..end as usize])
    } else {
        Some(&b[begin as usize..end as usize])
    }
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    const TEN_MIL_STR_CAP: usize = 10;
    fn new() -> Self {
        Self { a: vec![] }
    }
    fn merge(&mut self, page: usize, n: u64, carry: &mut u64) {
        if self.a.get(page).is_none() {
            self.a.push(0u64)
        }
        if let Some(con) = self.a.get_mut(page) {
            *con += n + *carry;
            if *con < Self::TEN_MIL {
                *carry = 0;
                return;
            }
            *carry = 1;
            *con -= Self::TEN_MIL;
        }
    }
    fn add(&mut self, b: &str) {
        let mut p = 0usize;
        let mut carry = 0u64;
        while let Some(s) = paging(&b, p, Self::TEN_MIL_STR_CAP) {
            let n = s.parse::<u64>().unwrap();
            self.merge(p, n, &mut carry);
            p += 1;
        }
        while carry != 0 {
            self.merge(p, 0, &mut carry);
            p += 1;
        }
    }
    fn head(&self, digits: u8) -> u64 {
        assert!(digits <= 10);
        let mut head = 0u64;
        for p in (0..self.a.len()).rev() {
            if let Some(&con) = self.a.get(p) {
                if head > u64::MAX / Self::TEN_MIL {
                    break;
                }
                head *= Self::TEN_MIL;
                head += con;
            }
        }
        let display_threshold = 10u64.pow(digits as u32);
        while head >= display_threshold {
            head /= 10;
        }
        head
    }
}

fn main() {
    let mut big_num = BigNum::new();
    for &b in FIFTY_DIGIT_NUMBERS.iter() {
        big_num.add(b);
    }
    let ans = big_num.head(10);

    println!("{}", ans);
    assert_eq!(ans, 5537376230);

    {
        let mut a = BigNum::new();
        for &b in vec!["5", "48", "125"].iter() {
            a.add(b);
        }
        assert_eq!(a.head(10), 178);
    }
    {
        let mut a = BigNum::new();
        let v = vec![
            "9999999999",
            "99999999999999999999",
            "40005484537376233",
            "3",
            "5537376230",
            "40000000000000"
        ];
        for &b in v.iter() {
            a.add(b);
        }
        assert_eq!(a.head(10), 1000400455);
    }
    {
        let mut a = BigNum::new();
        a.add(&"99999999999999999999");
        assert_eq!(a.head(10), 9999999999);
    }
}

const FIFTY_DIGIT_NUMBERS: [&str; 100] = [
    "37107287533902102798797998220837590246510135740250",
    "46376937677490009712648124896970078050417018260538",
    "74324986199524741059474233309513058123726617309629",
    "91942213363574161572522430563301811072406154908250",
    "23067588207539346171171980310421047513778063246676",
    "89261670696623633820136378418383684178734361726757",
    "28112879812849979408065481931592621691275889832738",
    "44274228917432520321923589422876796487670272189318",
    "47451445736001306439091167216856844588711603153276",
    "70386486105843025439939619828917593665686757934951",
    "62176457141856560629502157223196586755079324193331",
    "64906352462741904929101432445813822663347944758178",
    "92575867718337217661963751590579239728245598838407",
    "58203565325359399008402633568948830189458628227828",
    "80181199384826282014278194139940567587151170094390",
    "35398664372827112653829987240784473053190104293586",
    "86515506006295864861532075273371959191420517255829",
    "71693888707715466499115593487603532921714970056938",
    "54370070576826684624621495650076471787294438377604",
    "53282654108756828443191190634694037855217779295145",
    "36123272525000296071075082563815656710885258350721",
    "45876576172410976447339110607218265236877223636045",
    "17423706905851860660448207621209813287860733969412",
    "81142660418086830619328460811191061556940512689692",
    "51934325451728388641918047049293215058642563049483",
    "62467221648435076201727918039944693004732956340691",
    "15732444386908125794514089057706229429197107928209",
    "55037687525678773091862540744969844508330393682126",
    "18336384825330154686196124348767681297534375946515",
    "80386287592878490201521685554828717201219257766954",
    "78182833757993103614740356856449095527097864797581",
    "16726320100436897842553539920931837441497806860984",
    "48403098129077791799088218795327364475675590848030",
    "87086987551392711854517078544161852424320693150332",
    "59959406895756536782107074926966537676326235447210",
    "69793950679652694742597709739166693763042633987085",
    "41052684708299085211399427365734116182760315001271",
    "65378607361501080857009149939512557028198746004375",
    "35829035317434717326932123578154982629742552737307",
    "94953759765105305946966067683156574377167401875275",
    "88902802571733229619176668713819931811048770190271",
    "25267680276078003013678680992525463401061632866526",
    "36270218540497705585629946580636237993140746255962",
    "24074486908231174977792365466257246923322810917141",
    "91430288197103288597806669760892938638285025333403",
    "34413065578016127815921815005561868836468420090470",
    "23053081172816430487623791969842487255036638784583",
    "11487696932154902810424020138335124462181441773470",
    "63783299490636259666498587618221225225512486764533",
    "67720186971698544312419572409913959008952310058822",
    "95548255300263520781532296796249481641953868218774",
    "76085327132285723110424803456124867697064507995236",
    "37774242535411291684276865538926205024910326572967",
    "23701913275725675285653248258265463092207058596522",
    "29798860272258331913126375147341994889534765745501",
    "18495701454879288984856827726077713721403798879715",
    "38298203783031473527721580348144513491373226651381",
    "34829543829199918180278916522431027392251122869539",
    "40957953066405232632538044100059654939159879593635",
    "29746152185502371307642255121183693803580388584903",
    "41698116222072977186158236678424689157993532961922",
    "62467957194401269043877107275048102390895523597457",
    "23189706772547915061505504953922979530901129967519",
    "86188088225875314529584099251203829009407770775672",
    "11306739708304724483816533873502340845647058077308",
    "82959174767140363198008187129011875491310547126581",
    "97623331044818386269515456334926366572897563400500",
    "42846280183517070527831839425882145521227251250327",
    "55121603546981200581762165212827652751691296897789",
    "32238195734329339946437501907836945765883352399886",
    "75506164965184775180738168837861091527357929701337",
    "62177842752192623401942399639168044983993173312731",
    "32924185707147349566916674687634660915035914677504",
    "99518671430235219628894890102423325116913619626622",
    "73267460800591547471830798392868535206946944540724",
    "76841822524674417161514036427982273348055556214818",
    "97142617910342598647204516893989422179826088076852",
    "87783646182799346313767754307809363333018982642090",
    "10848802521674670883215120185883543223812876952786",
    "71329612474782464538636993009049310363619763878039",
    "62184073572399794223406235393808339651327408011116",
    "66627891981488087797941876876144230030984490851411",
    "60661826293682836764744779239180335110989069790714",
    "85786944089552990653640447425576083659976645795096",
    "66024396409905389607120198219976047599490197230297",
    "64913982680032973156037120041377903785566085089252",
    "16730939319872750275468906903707539413042652315011",
    "94809377245048795150954100921645863754710598436791",
    "78639167021187492431995700641917969777599028300699",
    "15368713711936614952811305876380278410754449733078",
    "40789923115535562561142322423255033685442488917353",
    "44889911501440648020369068063960672322193204149535",
    "41503128880339536053299340368006977710650566631954",
    "81234880673210146739058568557934581403627822703280",
    "82616570773948327592232845941706525094512325230608",
    "22918802058777319719839450180888072429661980811197",
    "77158542502016545090413245809786882778948721859617",
    "72107838435069186155435662884062257473692284509516",
    "20849603980134001723930671666823555245252804609722",
    "53503534226472524250874054075591789781264330331690",
];

struct Position {
    initial_number: u64,
    number_of_steps: u32,
}

struct Collatz {
    init_num: u64,
    next: Option<u64>,
    step_accum: u32,
    cache: Vec<u32>,
    max: Position,
}

impl Collatz {
    fn update_records(&mut self) {
        if let Some(s) = self.cache.get_mut(self.init_num as usize) {
            *s = self.step_accum;
        }
        if self.max.number_of_steps < self.step_accum {
            self.max.number_of_steps = self.step_accum;
            self.max.initial_number = self.init_num;
        }
    }
    fn move_along(&mut self) -> Option<u64> {
        let n = self.next?;
        if n == 1 {
            self.step_accum += 1;
            self.next = None;
            self.update_records();
            return self.next;
        }
        match self.cache.get(n as usize) {
            Some(r) if *r != 0 => {
                self.step_accum += 1 + *r;
                self.next = None;
                self.update_records();
                return self.next;
            }
            _ => (),
        }
        if n % 2 != 0 {
            self.step_accum += 2;
            self.next = Some((3 * n + 1) / 2);
            return self.next;
        }
        self.step_accum += 1;
        self.next = Some(n / 2);
        self.next
    }
    fn init_next(&mut self) {
        assert!(self.init_num > 1);
        self.next = if self.init_num % 2 == 0 {
            Some(self.init_num / 2)
        } else {
            Some(3 * self.init_num + 1)
        }
    }
}

fn main() {
    let mut c = Collatz {
        init_num: 0,
        next: None,
        step_accum: 0,
        cache: vec![0; 1_000_000],
        max: Position {
            initial_number: 1,
            number_of_steps: 0,
        },
    };

    for i in 500_000..1_000_000u64 {
        c.init_num = i;
        c.init_next();
        c.step_accum = 0;
        while c.move_along().is_some() {}
    }

    println!(
        "initial_number: {}, number_of_steps plus 1: {}",
        c.max.initial_number,
        c.max.number_of_steps + 1
    );
    assert_eq!(c.max.initial_number, 837799);
    assert_eq!(c.max.number_of_steps + 1, 525);
}

Problem 15 "Lattice paths"

Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.

How many such routes are there through a 20×20 grid?

問 15 「格子経路」

2×2 のマス目の左上からスタートした場合, 引き返しなしで右下にいくルートは 6 つある.

では, 20×20 のマス目ではいくつのルートがあるか.

struct Permutation {
    numerator: u8,
    denominator: u8,
}

impl Permutation {
    fn num(&self) -> u128 {
        let mut acc = 1u128;
        for i in self.denominator + 1..=self.numerator {
            acc *= i as u128;
        }
        acc
    }
}

struct Grid {
    width: u8,
    height: u8,
}

fn factorial(n: u8) -> u128 {
    match n {
        0 | 1 => 1,
        _ => factorial(n - 1) * n as u128,
    }
}

impl Grid {
    fn routes(&self) -> u64 {
        let a = Permutation {
            numerator: self.width + self.height,
            denominator: self.width,
        }
        .num();
        let b = factorial(self.height);
        (a / b) as u64
    }
}

fn main() {
    let r = Grid {
        width: 20,
        height: 20,
    }
    .routes();

    println!("{}", r);
    assert_eq!(r, 137846528820);
}

fn main() {
    let mut lattice = [[0u64; 22]; 22];
    lattice[1][1] = 1;
    for y in 1..lattice.len() {
        for x in 1..lattice.len() {
            lattice[y][x] += lattice[y - 1][x] + lattice[y][x - 1];
        }
    }
    let r = lattice[21][21];

    println!("{}", r);
    assert_eq!(r, 137846528820);
}

struct Combination {
    n: f64,
    k: f64,
}

impl Combination {
    fn _num(&self, n: f64, k: f64) -> f64 {
        if k == 1f64 {
            return n;
        }
        if k == 0f64 {
            return 1f64;
        }
        let prev = self._num(n, k - 1f64);
        prev * (n - k + 1f64) / k
    }
    fn num(&self) -> f64 {
        self._num(self.n, self.k)
    }
}

struct Grid {
    width: u8,
    height: u8,
}

impl Grid {
    fn routes(&self) -> u64 {
        Combination{
            n: (self.width + self.height) as f64,
            k: self.width as f64,
        }
        .num().ceil() as u64
    }
}

fn main() {
    let r = Grid {
        width: 20,
        height: 20,
    }
    .routes();

    println!("{}", r);
    assert_eq!(r, 137846528820);
}

struct Combination {
    n: f64,
    k: f64,
}

impl Combination {
    fn num(&self) -> f64 {
        assert!(self.n == 2f64 * self.k);
        (1..=self.k as usize)
            .map(|x| x as f64)
            .map(|x| (self.k + x) / x)
            .product::<f64>()
    }
}

struct Grid {
    width: u8,
    height: u8,
}

impl Grid {
    fn routes(&self) -> u64 {
        Combination{
            n: (self.width + self.height) as f64,
            k: self.width as f64,
        }
        .num().ceil() as u64
    }
}

fn main() {
    let r = Grid {
        width: 20,
        height: 20,
    }
    .routes();

    println!("{}", r);
    assert_eq!(r, 137846528820);
}

fn main() {
    let mut b = 1u64;
    for i in 1..=20 {
        b *= i;
    }
    let mut ab = 1f64 / b as f64;
    for i in 21..=40 {
        ab *= i as f64;
    }
    println!("{}", ab);
    assert_eq!(ab.ceil() as u64, 137846528820);
}

fn main() {
    let b = 1f64 / (1..=20).product::<u64>() as f64;
    let ab = (21..=40).fold(b, |p, i| p * i as f64);
    println!("{}", ab);
    assert_eq!(ab.ceil() as u64, 137846528820);
}

• Q.13. Large sum

struct BigNum {
    v: Vec<u64>,
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    fn double(&mut self) {
        let mut carry = 0u64;
        for con in self.v.iter_mut() {
            *con *= 2;
            *con += carry;
            if *con < Self::TEN_MIL {
                carry = 0;
                continue;
            }
            carry = 1;
            *con -= Self::TEN_MIL;
        }
        if carry != 0 {
            self.v.push(1u64);
        }
    }
    fn sum_of_digits(&self) -> u32 {
        let mut sum = 0u32;
        for &con in &self.v {
            let mut t = con;
            while t > 0 {
                sum += (t % 10) as u32;
                t /= 10;
            }
        }
        sum
    }
}

fn main() {
    let mut n = BigNum { v: vec![1] };
    for _ in 0..1000 {
        n.double();
    }
    let ans = n.sum_of_digits();

    println!("{}", ans);
    assert_eq!(ans, 1366);
}

const ZERO_TO_19: [&str; 20] = [
    "",
    "one",
    "two",
    "three",
    "four",
    "five",
    "six",
    "seven",
    "eight",
    "nine",
    "ten",
    "eleven",
    "twelve",
    "thirteen",
    "fourteen",
    "fifteen",
    "sixteen",
    "seventeen",
    "eighteen",
    "nineteen",
];

const ZERO_TO_90: [&str; 10] = [
    "", "", "twenty", "thirty", "forty", "fifty", "sixty", "seventy", "eighty", "ninety",
];

fn count_words(i: usize) -> u32 {
    match i {
        0..=19 => ZERO_TO_19[i].len() as u32,
        20..=99 => {
            let p1 = i % 10;
            let p2 = i / 10;
            (ZERO_TO_90[p2].len() + ZERO_TO_19[p1].len()) as u32
        }
        _ if i % 100 == 0 && i != 1000 => {
            let d = i / 100;
            (ZERO_TO_19[d].len() + "hundred".len()) as u32
        }
        101..=999 => {
            let p3 = i / 100;
            let p2p1 = i - p3 * 100;
            (ZERO_TO_19[p3].len() + "hundredand".len()) as u32 + count_words(p2p1)
        }
        1000 => ("onethousand".len()) as u32,
        _ => 0,
    }
}

fn main() {
    let mut sum = 0u32;
    for i in 1..=1000 {
        sum += count_words(i);
    }

    println!("{}", sum);
    assert_eq!(sum, 21124);
}

fn main() {
    let mut triangle: Vec<Vec<u16>> = vec![
        vec![75],
        vec![95, 64],
        vec![17, 47, 82],
        vec![18, 35, 87, 10],
        vec![20, 4, 82, 47, 65],
        vec![19, 1, 23, 75, 3, 34],
        vec![88, 2, 77, 73, 7, 63, 67],
        vec![99, 65, 4, 28, 6, 16, 70, 92],
        vec![41, 41, 26, 56, 83, 40, 80, 70, 33],
        vec![41, 48, 72, 33, 47, 32, 37, 16, 94, 29],
        vec![53, 71, 44, 65, 25, 43, 91, 52, 97, 51, 14],
        vec![70, 11, 33, 28, 77, 73, 17, 78, 39, 68, 17, 57],
        vec![91, 71, 52, 38, 17, 14, 91, 43, 58, 50, 27, 29, 48],
        vec![63, 66, 4, 68, 89, 53, 67, 30, 73, 16, 69, 87, 40, 31],
        vec![4, 62, 98, 27, 23, 9, 70, 98, 73, 93, 38, 53, 60, 4, 23],
    ];
    triangle.push(vec![0; triangle.last().unwrap().len() + 1]);
    for y in (0..triangle.len() - 1).rev() {
        for x in 0..triangle[y].len() {
            let a = triangle[y + 1][x];
            let b = triangle[y + 1][x + 1];
            triangle[y][x] += std::cmp::max(a, b);
        }
    }
    let sum = triangle[0][0];

    println!("{}", sum);
    assert_eq!(sum, 1074);
}

fn length_of_february(year: u16) -> u8 {
    if (year % 4 == 0 && year % 100 != 0) || year % 400 == 0 {
        29
    } else {
        28
    }
}

struct FirstDayOfMonth {
    year: u16,
    month: u8,
    day_count: u64,
    sunday_count: u32,
}

impl FirstDayOfMonth {
    fn new() -> Self {
        Self {
            year: 1900,
            month: 1,
            day_count: 0,
            sunday_count: 0,
        }
    }
    fn is_sunday(&self) -> bool {
        self.day_count % 7 == 6
    }
    fn next_month(&mut self) {
        self.day_count += match self.month {
            2 => length_of_february(self.year) as u64,
            4 | 6 | 9 | 11 => 30,
            _ => 31,
        };
        if self.month == 12 {
            self.year += 1;
            self.month = 1;
        } else {
            self.month += 1;
        }
        if self.year != 1900 && self.is_sunday() {
            self.sunday_count += 1;
        }
    }
}

fn main() {
    let mut cal = FirstDayOfMonth::new();
    while !(cal.year == 2000 && cal.month == 12) {
        cal.next_month();
    }
    let sum = cal.sunday_count;

    println!("{}", sum);
    assert_eq!(sum, 171);
}

#[derive(PartialEq)]
enum Weekday {
    Mon,
    Tue,
    Wed,
    Thu,
    Fri,
    Sat,
    Sun,
}

fn zeller_congruence(mut y: u32, mut m: u32, d: u32) -> Weekday {
    if m == 1 || m == 2 {
        m += 12;
        y -= 1;
    }
    let yd = y / 100;
    let ym = y % 100;
    match (d + (26 * (m + 1)) / 10 + ym + ym / 4 + yd / 4 + 5 * yd) % 7 {
        0 => Weekday::Sat,
        1 => Weekday::Sun,
        2 => Weekday::Mon,
        3 => Weekday::Tue,
        4 => Weekday::Wed,
        5 => Weekday::Thu,
        6 => Weekday::Fri,
        _ => panic!(),
    }
}

fn main() {
    let mut sum = 0u32;
    for y in 1901u32..=2000 {
        for m in 1u32..=12 {
            let weekday = zeller_congruence(y, m, 1);
            if weekday == Weekday::Sun {
                sum += 1;
            }
        }
    }

    println!("{}", sum);
    assert_eq!(sum, 171);
}

• Q.13 Large sum
• Q.16 Power digit sum

struct BigNum {
    v: Vec<u64>,
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    fn factorial(&mut self) {
        assert!(self.v.len() == 1);
        let up = self.v[0];
        assert!(((u64::MAX as f32 - Self::TEN_MIL as f32) / Self::TEN_MIL as f32) > (up as f32));
        for b in 2..up {
            self._multiply(b);
        }
    }
    fn _multiply(&mut self, b: u64) {
        let mut carry = 0u64;
        for con in self.v.iter_mut() {
            *con *= b;
            *con += carry;
            if *con < Self::TEN_MIL {
                carry = 0;
                continue;
            }
            carry = *con / Self::TEN_MIL;
            *con -= carry * Self::TEN_MIL;
        }
        if carry != 0 {
            self.v.push(carry);
        }
    }
    fn sum_of_digits(&self) -> u32 {
        let mut sum = 0u32;
        for &con in &self.v {
            let mut t = con;
            while t > 0 {
                sum += (t % 10) as u32;
                t /= 10;
            }
        }
        sum
    }
}

fn main() {
    let mut a = BigNum { v: vec![100u64] };
    a.factorial();
    let sum = a.sum_of_digits();

    println!("{}", sum);
    assert_eq!(sum, 648);
}

• Q.12 Highly divisible triangular number

struct AmicableNumberScanner {
    below: u32,
    _primes: Vec<u32>,
    _aliquot_sum: Vec<u32>,
}

impl AmicableNumberScanner {
    fn new(below: u32) -> Self {
        Self {
            below: below,
            _primes: vec![2, 3],
            _aliquot_sum: vec![0u32; below as usize],
        }
    }
    fn _divide_fully(&self, n: &mut u32, d: u32, side: &mut u32, sum: &mut u32) {
        if *n % d != 0 {
            return;
        }
        let mut exp = 0u32;
        while {
            *n /= d;
            exp += 1;
            *n % d == 0
        } {}
        *side = (*n as f32).sqrt() as u32;
        *sum *= (d.pow(exp + 1) - 1) / (d - 1);
    }
    fn _sum_of_divisors(&mut self, mut n: u32) -> u32 {
        let mut side = (n as f32).sqrt() as u32;
        let mut sum = 1u32;
        for &p in &self._primes {
            if p > side || n == 1 {
                break;
            }
            self._divide_fully(&mut n, p, &mut side, &mut sum);
        }
        if n != 1 {
            sum *= (n * n - 1) / (n - 1);
            self._primes.push(n);
        }
        sum
    }
    fn pair_sum(&mut self) -> u32 {
        for n in 4..self.below {
            self._aliquot_sum[n as usize] = self._sum_of_divisors(n) - n;
        }
        let mut sum = 0u32;
        for (i, v) in &self._aliquot_sum.enumerate() {
            let vsize = *v as usize;
            if vsize >= self._aliquot_sum.len() {
                continue;
            }
            if vsize == i {
                continue;
            }
            if self._aliquot_sum[vsize] == i as u32 {
                sum += *v;
            }
        }
        sum
    }
}

fn main() {
    let sum = AmicableNumberScanner::new(10_000).pair_sum();

    println!("{}", sum);
    assert_eq!(sum, 31626);
}

• Q.10 Summation of primes

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let sqrt = (sieve.len() as f32).sqrt() as usize;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            primes.push(index.i as u32);
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            primes.push(index.i as u32);
        }
        index.increment();
    }
    primes
}

struct AmicableNumberScanner {
    below: u32,
    _primes: Vec<u32>,
    _checked: Vec<bool>,
}

impl AmicableNumberScanner {
    fn new(below: u32) -> Self {
        Self {
            below: below,
            _primes: primes(below),
            _checked: vec![false; below as usize],
        }
    }
    fn _divide_fully(&self, n: &mut u32, d: u32, side: &mut u32, sum: &mut u32) {
        if *n % d != 0 {
            return;
        }
        let mut exp = 0u32;
        while {
            *n /= d;
            exp += 1;
            *n % d == 0
        } {}
        *side = (*n as f32).sqrt() as u32;
        *sum *= (d.pow(exp + 1) - 1) / (d - 1);
    }
    fn _sum_of_divisors(&mut self, mut n: u32) -> u32 {
        let mut side = (n as f32).sqrt() as u32;
        let mut sum = 1u32;
        for &p in self._primes.iter() {
            if p > side || n == 1 {
                break;
            }
            self._divide_fully(&mut n, p, &mut side, &mut sum);
        }
        if n != 1 {
            sum *= (n * n - 1) / (n - 1);
        }
        sum
    }
    fn pair_sum(&mut self) -> u32 {
        let mut pair_sum = 0u32;
        for a in 4..self.below {
            if self._checked[a as usize] {
                continue;
            }
            let sum = self._sum_of_divisors(a) - a;
            if sum <= a {
                continue;
            }
            if sum >= self.below {
                continue;
            }
            let b = self._sum_of_divisors(sum) - sum;
            self._checked[sum as usize] = true;
            if a == b {
                pair_sum += a + sum;
            }
        }
        pair_sum
    }
}

fn main() {
    let sum = AmicableNumberScanner::new(10_000).pair_sum();

    println!("{}", sum);
    assert_eq!(sum, 31626);
}

• mycodeschool - Sorting Algorithms, youtube playlist

Because the original name list is very long, these examples have only a part of it.

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

1. Quick sort

fn median<'a>(vec: &[&'a str], a: usize, c: usize) -> &'a str {
    let b = (c - a) / 2;
    let (astr, bstr, cstr) = (vec[a], vec[b], vec[c]);
    if (cstr < astr && astr < bstr) || (bstr <= astr && astr < cstr) {
        astr
    } else if (astr < bstr && bstr < cstr) || (cstr < bstr && bstr <= astr) {
        bstr
    } else {
        cstr
    }
}

fn met(sinker_depth: usize, float_depth: usize) -> bool {
    sinker_depth >= float_depth
}

fn sink_fully(vec: &[&str], depth: &mut usize, blocker: &str) {
    while vec[*depth] < blocker {
        *depth += 1;
    }
}

fn float_fully(vec: &[&str], depth: &mut usize, blocker: &str) {
    while vec[*depth] > blocker {
        *depth -= 1;
    }
}

fn break_through(vec: &mut [&str], sinker_depth: &mut usize, float_depth: &mut usize) {
    vec.swap(*sinker_depth, *float_depth);
    *sinker_depth += 1;
    *float_depth -= 1;
}

fn release(vec: &mut [&str], sinker0: usize, float0: usize) {
    if met(sinker0, float0) {
        return;
    }
    match float0 - sinker0 {
        1 => {
            if vec[sinker0] > vec[sinker0 + 1] {
                vec.swap(sinker0, sinker0 + 1);
            }
            return;
        }
        2 => {
            if vec[sinker0] > vec[sinker0 + 1] {
                vec.swap(sinker0, sinker0 + 1);
            }
            if vec[sinker0 + 1] > vec[sinker0 + 2] {
                vec.swap(sinker0 + 1, sinker0 + 2);
            }
            if vec[sinker0] > vec[sinker0 + 1] {
                vec.swap(sinker0, sinker0 + 1);
            }
            return;
        }
        _ => (),
    }
    let pivot = median(vec, sinker0, float0);
    let mut sinker = sinker0;
    let mut float = float0;
    loop {
        sink_fully(vec, &mut sinker, pivot);
        float_fully(vec, &mut float, pivot);
        if met(sinker, float) {
            break;
        }
        break_through(vec, &mut sinker, &mut float);
    }
    println!("pivot: {}", pivot);
    println!("{:#?}", &vec[sinker0..=sinker - 1]);
    println!("{:#?}", &vec[float + 1..=float0]);
    release(vec, sinker0, sinker - 1);
    release(vec, float + 1, float0);
}

fn quick_sort(vec: &mut [&str]) {
    release(vec, 0, vec.len() - 1);
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    quick_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

TODO: switch to the insertion sort when 90 elements have been sorted by the quick sort

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

2. Merge sort

fn drain_into<'a>(a: &[&'a str], b: &[&'a str], ab: &mut [&'a str]) {
    let (mut x, mut y, mut i) = (0, 0, 0);
    while x < a.len() && y < b.len() {
        if a[x] < b[y] {
            ab[i] = a[x];
            x += 1;
        } else {
            ab[i] = b[y];
            y += 1;
        }
        i += 1;
    }
    if x < a.len() {
        ab[i..].copy_from_slice(&a[x..]);
    }
    if y < b.len() {
        ab[i..].copy_from_slice(&b[y..]);
    }
}

fn merge_sort(segment: &mut [&str]) {
    let n = segment.len();
    let m = n / 2;
    if n <= 1 {
        return;
    }
    merge_sort(&mut segment[0..m]);
    merge_sort(&mut segment[m..n]);
    println!("---\n{:#?}", &segment[0..m]);
    println!("{:#?}", &segment[m..n]);

    let mut tmp: Vec<&str> = segment.to_vec();
    drain_into(&segment[0..m], &segment[m..n], &mut tmp[..]);
    segment.copy_from_slice(&tmp);
    println!("{:#?}", &segment);
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    merge_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

3. Heap sort

fn heapify(arr: &mut [&str], pi: usize) {
    let lef = 2 * pi + 1;
    let rig = lef + 1;
    if lef >= arr.len() {
        return;
    }
    let max = if rig >= arr.len() {
        lef
    } else if arr[lef] >= arr[rig] {
        lef
    } else {
        rig
    };
    if arr[pi] < arr[max] {
        arr.swap(pi, max);
        println!("---\n     {}", &arr[pi]);
        println!("{}/\\{}", &arr.get(lef).unwrap_or(&"{}"), &arr.get(rig).unwrap_or(&"{}"));
        heapify(arr, max);
    }
}

fn build_heap(arr: &mut [&str]) {
    let parental_indice = 0..arr.len() / 2;
    for pi in parental_indice.rev() {
        heapify(arr, pi);
    }
}

fn serialize(arr: &mut [&str]) {
    for edge in (1..arr.len()).rev() {
        arr.swap(0, edge);
        println!("---\n{:#?}", &arr[edge..]);
        heapify(&mut arr[..edge], 0);
    }
}

fn heap_sort(arr: &mut [&str]) {
    build_heap(arr);
    print_heap(arr);
    serialize(arr);
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    heap_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

fn print_heap(arr: &[&str]) {
    fn print_white_space(n: usize) {
        for _ in 0..n {
            print!(" ");
        }
    }
    let height = ((arr.len() + 1) as f32).log2() as usize + 1;
    let cell = arr
        .iter()
        .map(|&s| s.len())
        .reduce(|a, b| std::cmp::max(a, b))
        .unwrap();
    let width = cell * 2usize.pow(height as u32);
    let mut levels: Vec<Vec<String>> = vec![vec![]; height + 1];

    for (i, &v) in arr.iter().enumerate() {
        let h = ((i + 1) as f32).log2() as usize + 1;
        let r = levels.get_mut(h).unwrap();
        r.push(format!("{}({})", v, i));
    }
    let last = levels.last_mut().unwrap();
    while last.len() < 2usize.pow(height as u32 - 1) {
        last.push(String::new());
    }
    for r in levels {
        if r.len() == 0 {
            continue;
        }
        let space = (width) / r.len();
        print_white_space(space / 2);
        for (i, c) in r.iter().enumerate() {
            let arrow1 = if i % 2 == 0 { "" } else { "\\" };
            let arrow2 = if i % 2 != 0 { "" } else { "/" };
            print!("{}{}{}", arrow1, c, arrow2);
            print_white_space(space - c.len() - 1);
        }
        println!()
    }
}

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

4. Bubble sort

fn bubble_sort(vec: &mut Vec<&str>) {
    for i in 0..vec.len() {
        let mut swap_was_required = false;
        for j in 0..vec.len() - i - 1 {
            if vec[j] > vec[j + 1] {
                vec.swap(j, j + 1);
                swap_was_required = true;
            }
        }
        println!("---\n{:#?}", &vec[0..vec.len() - i - 1]);
        println!("{:#?}", &vec[vec.len() - i - 1..vec.len()]);
        if !swap_was_required {
            break;
        }
    }
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    bubble_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

5. Selection sort

fn selection_sort(vec: &mut Vec<&str>) {
    for i in 0..vec.len() {
        let mut min_index = i;
        for j in (i + 1)..vec.len() {
            if vec[j] < vec[min_index] {
                min_index = j;
            }
        }
        vec.swap(i, min_index);
        println!("---\n{:#?}", &vec[0..=i]);
        println!("{:#?}", &vec[std::cmp::min(i + 1, vec.len())..vec.len()]);
    }
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    selection_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

• 1. Go to Quick sort
• 2. Go to Merge sort
• 3. Go to Heap sort
• 4. Go to Bubble sort
• 5. Go to Selection sort
• 6. Go to Insertion sort

6. Insertion sort

fn insertion_sort(vec: &mut [&str]) {
    for i in 0..vec.len() {
        for j in (0..i).rev() {
            if vec[j] < vec[j + 1] {
                break;
            }
            vec.swap(j, j + 1);
        }
        println!("---\n{:#?}", &vec[0..=i]);
        println!("{:#?}", &vec[i + 1..vec.len()]);
    }
}

fn name_score(index: usize, name: &str) -> u32 {
    let position = index as u32 + 1;
    let worth = name.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>();
    position * worth
}

fn main() {
    let mut names = NAMES.to_vec();
    insertion_sort(&mut names);
    let sum: u32 = names
        .iter()
        .enumerate()
        .map(|(i, &n)| name_score(i, n))
        .sum();

    println!("---\n{:#?}", names);
    println!("{}", sum);
    assert_eq!(sum, 26578);
}

const NAMES: &[&str] = &[
    "MARY",
    "PATRICIA",
    "LINDA",
    "BARBARA",
    "ELIZABETH",
    "JENNIFER",
    "MARIA",
    "SUSAN",
    "MARGARET",
    "DOROTHY",
    "LISA",
    "NANCY",
    "KAREN",
    "BETTY",
    "HELEN",
    "SANDRA",
    "DONNA",
    "CAROL",
    "RUTH",
    "SHARON",
    "MICHELLE",
    "LAURA",
    "SARAH",
    "KIMBERLY",
    "DEBORAH",
    "JESSICA",
    "SHIRLEY",
    "CYNTHIA",
];

• Q.21 Amicable numbers

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let sqrt = (sieve.len() as f32).sqrt() as usize;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            primes.push(index.i as u32);
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            primes.push(index.i as u32);
        }
        index.increment();
    }
    primes
}

struct AbundantNumberScanner {
    below: u32,
    _primes: Vec<u32>,
    _pair_sieve: Vec<bool>,
}

impl AbundantNumberScanner {
    fn new(below: u32) -> Self {
        Self {
            below: below,
            _primes: primes(below),
            _pair_sieve: vec![false; below as usize],
        }
    }
    fn _divide_fully(&self, n: &mut u32, d: u32, side: &mut u32, sum: &mut u32) {
        if *n % d != 0 {
            return;
        }
        let mut exp = 0u32;
        while {
            *n /= d;
            exp += 1;
            *n % d == 0
        } {}
        *side = (*n as f32).sqrt() as u32;
        *sum *= (d.pow(exp + 1) - 1) / (d - 1);
    }
    fn _sum_of_divisors(&mut self, mut n: u32) -> u32 {
        let mut side = (n as f32).sqrt() as u32;
        let mut sum = 1u32;
        for &p in self._primes.iter() {
            if p > side || n == 1 {
                break;
            }
            self._divide_fully(&mut n, p, &mut side, &mut sum);
        }
        if n != 1 {
            sum *= (n * n - 1) / (n - 1);
        }
        sum
    }
    fn init_abundant_num_pair_sieve(&mut self) {
        let mut abundant_numbers = vec![];
        for n in 12..self.below {
            let sum = self._sum_of_divisors(n) - n;
            if sum > n {
                abundant_numbers.push(n);
            }
        }
        for (i, &a) in abundant_numbers.iter().enumerate() {
            for &b in abundant_numbers[i..].iter() {
                if let Some(n) = self._pair_sieve.get_mut((a + b) as usize) {
                    *n = true;
                }
            }
        }
    }
    fn non_pair_sum(&mut self) -> u32 {
        let mut non_pair_sum = 0u32;
        for n in 1..self.below {
            if !self._pair_sieve[n as usize] {
                non_pair_sum += n;
            }
        }
        non_pair_sum
    }
}

fn main() {
    let mut a = AbundantNumberScanner::new(28_124);
    a.init_abundant_num_pair_sieve();
    let sum = a.non_pair_sum();

    println!("{}", sum);
    assert_eq!(sum, 4179871);
}

fn factorial(n: u64) -> u64 {
    match n {
        0 | 1 => 1,
        _ => factorial(n - 1) * n,
    }
}

fn main() {
    let mut reminder = 1_000_000u64 - 1;
    let mut items_with_order = vec![0u64, 1, 2, 3, 4, 5, 6, 7, 8, 9];
    let mut millionth_element = 0u64;
    for weight in (0..items_with_order.len()).rev() {
        let unit = factorial(weight as u64);
        let quot = reminder / unit;
        reminder -= quot * unit;
        millionth_element *= 10;
        millionth_element += items_with_order.remove(quot as usize);
    }

    println!("{}", millionth_element);
    assert_eq!(millionth_element, 2783915460);
}

fn main() {
    let constant_1 = (1f64 + 5f64.sqrt()).log10() - 2f64.log10();
    let constant_2 = 5f64.log10() / 2f64;
    let digits_of_nth_fibonacci = |nth: f64| -> f64 { nth * constant_1 - constant_2 };

    let ratio = (1f64 + 5f64.sqrt()) / 2f64;
    let iteration = 10f64.log(ratio);
    let estimation = iteration * 999f64;
    println!("estimation: {} th Fibonacci number would have 1000 digits", estimation);
    let mut n = (estimation - iteration).floor(); // rollback to 999 digits
    assert!(digits_of_nth_fibonacci(n) < 999f64);
    while digits_of_nth_fibonacci(n) < 999f64 {
        n += 1f64;
    }

    println!("{}", n);
    assert_eq!(n as u32, 4782);
}

• 1. Go to a solution using the long division
• 2. Go to a solution using prime numbers
• 3. Go to a solution using the mod_pow function against the divisors of p-1
• 4. Go to reference

1. Long division

struct UnitFraction {
    reciprocal: u32,
    repetend_length: u32,
}

fn is_recurring(mut n: u32) -> bool {
    if n % 2 != 0 && n % 5 != 0 {
        return true;
    }
    for &d in [2u32, 5].iter() {
        while n % d == 0 {
            n /= d;
        }
        if n == 1 {
            return false;
        }
    }
    true
}

fn repetend_length(n: u32, residue_history: &mut [u32]) -> u32 {
    assert!(residue_history.len() >= n as usize);
    let mut dividend = 1u32;
    for nth_time_around in 0u32.. {
        let residue = dividend % n;
        let last_time = residue_history[residue as usize];
        if last_time != 0 {
            return nth_time_around - last_time;
        }
        residue_history[residue as usize] = nth_time_around;
        dividend = residue * 10;
    }
    panic!("irrational number")
}

fn number_with_longest_recurring_cycle(below: u32) -> u32 {
    assert!(below > 3);
    let mut uf = UnitFraction {
        reciprocal: 1,
        repetend_length: 0,
    };
    let blank = vec![0u32; below as usize];
    let mut residue_history = vec![0u32; below as usize];
    for n in (1u32..below).rev() {
        if !is_recurring(n) {
            continue;
        }
        residue_history[..n as usize].copy_from_slice(&blank[..n as usize]);
        let length = repetend_length(n, &mut residue_history[0..n as usize]);
        if n - 1 == length {
            return n;
        }
        if length > uf.repetend_length {
            uf.repetend_length = length;
            uf.reciprocal = n;
        }
    }
    uf.reciprocal
}

fn main() {
    let num = number_with_longest_recurring_cycle(1000);
    println!("{}", num);
    assert_eq!(num, 983);

    assert_eq!(number_with_longest_recurring_cycle(10000), 9967);
    assert_eq!(number_with_longest_recurring_cycle(9968), 9967);
    assert_eq!(number_with_longest_recurring_cycle(5000), 4967);
    assert_eq!(number_with_longest_recurring_cycle(8), 7);
    assert_eq!(number_with_longest_recurring_cycle(20), 19);
    assert_eq!(number_with_longest_recurring_cycle(18), 17);
    assert_eq!(number_with_longest_recurring_cycle(25), 23);
    assert_eq!(number_with_longest_recurring_cycle(6), 3);
}

• 1. Go to a solution using the long division
• 2. Go to a solution using prime numbers
• 3. Go to a solution using the mod_pow function against the divisors of p-1
• 4. Go to reference

2. Prime numbers

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let sqrt = (sieve.len() as f32).sqrt() as usize;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            primes.push(index.i as u32);
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            primes.push(index.i as u32);
        }
        index.increment();
    }
    primes
}

fn repetend_length(n: u32) -> u32 {
    assert!(n % 2 != 0 && n % 5 != 0);
    let mut dividend = 10u32;
    for nth_time_around in 1u32.. {
        let residue = dividend % n;
        if residue == 1 {
            return nth_time_around
        }
        dividend = residue * 10;
    }
    panic!("irrational number")
}

fn number_with_longest_recurring_cycle(below: u32) -> u32 {
    if below < 7 {
        return 3;
    }
    let primes = primes(below);
    for &p in primes.iter().rev() {
        if repetend_length(p) == p - 1 {
            return p;
        }
    }
    panic!("couldn't find a point that n - 1 == repetend_length(n)")
}

fn main() {
    let num = number_with_longest_recurring_cycle(1000);
    println!("{}", num);
    assert_eq!(num, 983);

    assert_eq!(number_with_longest_recurring_cycle(10000), 9967);
    assert_eq!(number_with_longest_recurring_cycle(9968), 9967);
    assert_eq!(number_with_longest_recurring_cycle(5000), 4967);
    assert_eq!(number_with_longest_recurring_cycle(8), 7);
    assert_eq!(number_with_longest_recurring_cycle(20), 19);
    assert_eq!(number_with_longest_recurring_cycle(18), 17);
    assert_eq!(number_with_longest_recurring_cycle(25), 23);
    assert_eq!(number_with_longest_recurring_cycle(6), 3);
}

• 1. Go to a solution using the long division
• 2. Go to a solution using prime numbers
• 3. Go to a solution using the mod_pow function against the divisors of p-1
• 4. Go to reference

3. Divisors of p-1 and modular exponentiation

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let sqrt = (sieve.len() as f32).sqrt() as usize;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            primes.push(index.i as u32);
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            primes.push(index.i as u32);
        }
        index.increment();
    }
    primes
}

fn mod_pow(mut a: u32, mut exp: u32, m: u32) -> u32 {
    if m == 1 {
        return 0;
    }
    if exp == 0 {
        return 1;
    }
    let mut result = 1;
    a %= m;
    loop {
        if exp % 2 == 1 {
            result *= a;
            result %= m;
        }
        exp >>= 1;
        if exp == 0 {
            break;
        }
        a *= a;
        a %= m;
    }
    result
}

fn list_divisors(n: u32) -> Vec<u32> {
    let side = (n as f32).sqrt() as u32;
    let mut vec = vec![];
    for d in 1..=side {
        if n % d == 0 {
            vec.push(d);
            if d != side {
                vec.push(n / d);
            }
        }
    }
    vec.sort();
    vec
}

fn number_with_longest_recurring_cycle(below: u32) -> u32 {
    if below < 7 {
        return 3;
    }
    let primes = primes(below);
    'next_prime: for &p in primes.iter().rev() {
        let divisors = list_divisors(p - 1);
        for &d in &divisors[0..divisors.len() - 1] {
            if mod_pow(10, d, p) == 1 {
                continue 'next_prime;
            }
        }
        return p;
    }
    panic!("couldn't find a point that n - 1 == recurring_length(n)")
}

fn main() {
    let num = number_with_longest_recurring_cycle(1000);
    println!("{}", num);
    assert_eq!(num, 983);

    assert_eq!(number_with_longest_recurring_cycle(10000), 9967);
    assert_eq!(number_with_longest_recurring_cycle(9968), 9967);
    assert_eq!(number_with_longest_recurring_cycle(5000), 4967);
    assert_eq!(number_with_longest_recurring_cycle(8), 7);
    assert_eq!(number_with_longest_recurring_cycle(20), 19);
    assert_eq!(number_with_longest_recurring_cycle(18), 17);
    assert_eq!(number_with_longest_recurring_cycle(25), 23);
    assert_eq!(number_with_longest_recurring_cycle(6), 3);
}

• Binary Exponentiation - e2

• 1. Go to a solution using the long division

• 2. Go to a solution using prime numbers

• 3. Go to a solution using the mod_pow function against the divisors of p-1

• 4. Go to reference

Reference

• A001913 Full reptend primes: primes with primitive root 10.
• A007732 Period of decimal representation of 1/n.
• Q.21 Amicable numbers
• Q.2 Even Fibonacci numbers
• Youtube, Fermat’s HUGE little theorem, pseudoprimes and Futurama
• Youtube, Fool-Proof Test for Primes - Numberphile
• Project Euler & HackerRank Problem 26 Solution
• Binary Exponentiation - CP-Algorithms
• Our Primitive Roots, Chris Lyons, fullerton.edu

• en.wikipedia.org/wiki/Infinite_monkey_theorem

struct Sieve {
    _sieve: Vec<bool>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn init(&mut self) {
        let sqrt = (self._sieve.len() as f64).sqrt() as usize;
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index > sqrt {
                break;
            }
            if self._sieve[index] {
                self.rule_out(index);
            }
            index += i;
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self { _sieve: sieve };
        s.init();
        s
    }
    fn is_prime(&self, n: u32) -> bool {
        assert!(n < self._sieve.len() as u32);
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        self._sieve[n as usize]
    }
    fn primes(&self, below: u32) -> Vec<u32> {
        let mut primes: Vec<u32> = vec![2u32, 3u32];
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index >= below as usize {
                break;
            }
            if self._sieve[index] {
                primes.push(index as u32);
            }
            index += i;
        }
        primes
    }
}

fn quadratic_formula(n: u32, a: i32, b: u32) -> i32 {
    (n * n) as i32 + a * n as i32 + b as i32
}

fn main() {
    let (mut nmax, mut amax, mut bmax) = (1u32, 0i32, 0u32);
    let sieve = Sieve::new(2_000_000);
    for b in sieve.primes(1001) {
        for a in (-(b as i32) + 1)..=999 {
            let mut n = 1;
            let mut v = quadratic_formula(1, a, b);
            if !(v > 1 && sieve.is_prime(v as u32)) {
                continue;
            }
            while {
                n += 1;
                v = quadratic_formula(n, a, b);
                v > 1 && sieve.is_prime(v as u32)
            } {}
            if n > nmax {
                nmax = n;
                amax = a;
                bmax = b;
            }
        }
    }
    let product = amax * bmax as i32;

    println!("{}", product);
    assert_eq!(product, -59231);
}

21 22 23 24 25
20  7  8  9 10
19  6  1  2 11
18  5  4  3 12
17 16 15 14 13

• Q.6 Sum square difference

fn main() {
    let width = 1001u64;
    assert!(width % 2 == 1);
    let n = width / 2;
    let sum = 16 * n * (n + 1) * (2 * n + 1) / 6 + 4 * n * (1 + n) / 2 + 4 * n + 1;
    println!("{}", sum);
    assert_eq!(sum, 669171001);
}

• Q.21 Amicable numbers

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let sqrt = (sieve.len() as f32).sqrt() as usize;
    let mut index = Index::new();
    while index.i <= sqrt {
        if sieve[index.i] {
            primes.push(index.i as u32);
            rule_out(&mut sieve, index.i);
        }
        index.increment();
    }
    while index.i < sieve.len() {
        if sieve[index.i] {
            primes.push(index.i as u32);
        }
        index.increment();
    }
    primes
}

#[derive(PartialEq, Eq, PartialOrd, Ord, Clone, Debug)]
struct Factor {
    prime: u32,
    exp: u32,
}

fn divide_fully(n: &mut u32, d: u32, side: &mut u32, factors: &mut Vec<Factor>) {
    if *n % d != 0 {
        return;
    }
    let mut exp = 0u32;
    while {
        *n /= d;
        exp += 1;
        *n % d == 0
    } {}
    factors.push(Factor { prime: d, exp: exp });
    *side = (*n as f32).sqrt() as u32;
}

fn factorize(mut n: u32, primes: &[u32]) -> Vec<Factor> {
    let mut factors = vec![];
    let mut side = (n as f32).sqrt() as u32;
    for &p in primes.iter() {
        if p > side || n == 1 {
            break;
        }
        divide_fully(&mut n, p, &mut side, &mut factors);
    }
    if n != 1 {
        factors.push(Factor { prime: n, exp: 1 });
    }
    factors
}

fn count_duplication(arr: &mut [Vec<Factor>]) -> u32 {
    arr.sort();
    let mut dup = 0u32;
    for i in 1..arr.len() {
        if arr[i - 1] == arr[i] {
            dup += 1;
        }
    }
    dup
}

fn main() {
    let primes = primes(101);
    let mut expressions = Vec::new();
    (2..=100u32).map(|a| factorize(a, &primes)).for_each(|a| {
        for b in 2..=100u32 {
            let mut ab = a.to_vec();
            ab.iter_mut().for_each(|f| f.exp *= b);
            expressions.push(ab);
        }
    });
    let c = expressions.len() as u32 - count_duplication(&mut expressions);

    println!("{}", c);
    assert_eq!(c, 9183);
}

fn match_pow_sum(target: u32, pow_sum_999_fold: &[u32; 999]) -> bool {
    let mut digits = target;
    let mut sum = 0;
    while digits > 0 {
        let d = digits % 1000;
        digits /= 1000;
        if d == 0 {
            continue;
        }
        sum += pow_sum_999_fold[d as usize - 1];
        if sum > target {
            return false;
        }
    }
    sum == target
}

fn pow_sum_999_fold(power_ninefold: &[u32; 9]) -> [u32; 999] {
    let mut pow_sum_999_fold = [0u32; 999];
    for i in 1..=pow_sum_999_fold.len() {
        let mut sum = 0;
        let mut digits = i as u32;
        while digits > 0 {
            let d = digits % 10;
            digits /= 10;
            if d != 0 {
                sum += power_ninefold[d as usize - 1];
            }
        }
        pow_sum_999_fold[i - 1] = sum;
    }
    pow_sum_999_fold
}

fn digit_range_max(powed_nine: u32) -> u32 {
    let mut digit_min = 1u32;
    let mut pow_sum_max = powed_nine;
    while digit_min < pow_sum_max {
        digit_min *= 10;
        pow_sum_max += powed_nine;
    }
    pow_sum_max - powed_nine
}

fn main() {
    let e = 5;
    let mut power_ninefold = [0u32; 9];
    (1..=9u32).for_each(|n| power_ninefold[n as usize - 1] = n.pow(e));
    let pow_sum_999_fold = pow_sum_999_fold(&power_ninefold);
    let digits_max = digit_range_max(power_ninefold[8]);
    let sum = (2..=digits_max)
        .filter(|&d| match_pow_sum(d, &pow_sum_999_fold))
        .sum::<u32>();

    println!("{}", sum);
    assert_eq!(sum, 443839);
}

use std::cmp::Ordering;

fn coin_change_combination(payment: usize, coins: &[usize]) -> u32 {
    assert!(payment > 0 && coins.len() > 0);
    let mut table = vec![vec![0u32; payment]; coins.len()];
    for c in 0..table.len() {
        for p in 0..table[c].len() {
            let v_no = if c == 0 { 0u32 } else { table[c - 1][p] };
            let v_we = match (p + 1).partial_cmp(&(coins[c])).expect("NaNs") {
                Ordering::Less => 0u32,
                Ordering::Equal => 1u32,
                Ordering::Greater => table[c][p - coins[c]],
            };
            table[c][p] = v_no + v_we;
        }
    }
    table[coins.len() - 1][payment - 1]
}

fn main() {
    let payment = 200usize;
    let coins = [1usize, 2, 5, 10, 20, 50, 100, 200];
    let comb = coin_change_combination(payment, &coins);

    println!("{}", comb);
    assert_eq!(comb, 73682);
    assert_eq!(coin_change_combination(8, &[1, 3, 5, 7]), 6);
    assert_eq!(coin_change_combination(3, &[1, 2]), 2);
    assert_eq!(coin_change_combination(2, &[1, 2]), 2);
    assert_eq!(coin_change_combination(1, &[1, 2]), 1);
    assert_eq!(coin_change_combination(5, &[2, 3]), 1);
    assert_eq!(coin_change_combination(5, &[1, 2, 3]), 5);
    assert_eq!(coin_change_combination(5, &[1]), 1);
    assert_eq!(coin_change_combination(2, &[3]), 0);
}

use std::ops::RangeInclusive;

fn is_pandigital(a: u32, b: u32, ab: u32) -> bool {
    let mut bits = 0u16;
    for n in [a, b, ab].iter_mut() {
        while *n > 0 {
            let d = *n % 10;
            bits |= 1 << d;
            *n /= 10;
        }
    }
    bits == 0b1111111110u16
}

fn sum_distinct(arr: &mut [u32]) -> u32 {
    arr.sort();
    let mut sum = 0u32;
    if let Some(&n) = arr.get(0) {
        sum += n;
    }
    for i in 1..arr.len() {
        if arr[i - 1] != arr[i] {
            sum += arr[i];
        }
    }
    sum
}

fn explore_pandigital_combinations(
    a: RangeInclusive<u32>,
    b: RangeInclusive<u32>,
    products: &mut Vec<u32>,
) {
    for a in a {
        for b in b.clone() {
            let ab = a * b;
            if ab > 9876 {
                break;
            }
            if is_pandigital(a, b, ab) {
                products.push(ab);
            }
        }
    }
}

fn main() {
    let mut products = Vec::<u32>::new();
    explore_pandigital_combinations(2..=9, 1234..=9876, &mut products);
    explore_pandigital_combinations(12..=98, 123..=987, &mut products);
    let sum = sum_distinct(&mut products);

    println!("{}", sum);
    assert_eq!(sum, 45228);
}

fn gcd(mut a: u32, mut b: u32) -> u32 {
    assert!(a != 0 && b != 0);
    while b != 0 {
        let r = a % b;
        a = b;
        b = r;
    }
    a
}

fn main() {
    let mut numerator = 1u32;
    let mut denominator = 1u32;
    for a in 1u32..=9 {
        for c in a..=9 {
            for d in a..c {
                if (10 * a + c) * d == (10 * c + d) * a && a != d {
                    numerator *= a;
                    denominator *= d;
                }
            }
        }
    }
    let gcd = gcd(numerator, denominator);
    let ans = denominator / gcd;

    println!("{}", ans);
    assert_eq!(ans, 100);
}

• Q.30 Digit fifth powers

fn build_factorial_tenfold() -> [u32; 10] {
    let mut acc = 1u32;
    let mut factorial_tenfold = [1u32; 10];
    for n in 1..=9 {
        acc *= n;
        factorial_tenfold[n as usize] = acc;
    }
    factorial_tenfold
}

fn factorial_sum_10000_fold(factorial_tenfold: &[u32; 10]) -> [u32; 10000] {
    let mut factorial_sum_10000_fold = [0u32; 10000];
    factorial_sum_10000_fold[0] = 1;
    for i in 1..factorial_sum_10000_fold.len() {
        let mut sum = 0;
        let mut digits = i as u32;
        while digits > 0 {
            let d = digits % 10;
            digits /= 10;
            sum += factorial_tenfold[d as usize];
        }
        factorial_sum_10000_fold[i] = sum;
    }
    factorial_sum_10000_fold
}

fn zero_pad_10000(carry: u32, residue: u32, sum: &mut u32) {
    match (carry > 0, residue) {
        (false, _) => (),
        (true, 0..=9) => *sum += 3,
        (true, 10..=99) => *sum += 2,
        (true, 100..=999) => *sum += 1,
        _ => (),
    }
}

fn match_factorial_sum_10000(target: u32, factorial_sum_10000_fold: &[u32; 10000]) -> bool {
    let mut digits = target;
    let mut sum = 0;
    while digits > 0 {
        let d = digits % 10000;
        digits /= 10000;
        sum += factorial_sum_10000_fold[d as usize];
        zero_pad_10000(digits, d, &mut sum);
        if sum > target {
            return false;
        }
    }
    sum == target
}

fn digit_range_max(fact_nine: u32) -> u32 {
    let mut digit_min = 1u32;
    let mut fact_sum_max = fact_nine;
    while digit_min < fact_nine {
        digit_min *= 10;
        fact_sum_max += fact_nine;
    }
    fact_sum_max - fact_nine
}

fn main() {
    let factorial_tenfold = build_factorial_tenfold();
    let factorial_sum_10000_fold = factorial_sum_10000_fold(&factorial_tenfold);
    let digit_range_max = digit_range_max(factorial_tenfold[9]);
    let sum = (3..digit_range_max)
        .filter(|&d| match_factorial_sum_10000(d, &factorial_sum_10000_fold)) 
        .sum::<u32>();

    println!("{}", sum);
    assert_eq!(sum, 40730);
}

• Q.27 Quadratic primes
• Q.7 10001st prime

struct Sieve {
    _sieve: Vec<bool>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn init(&mut self) {
        let sqrt = (self._sieve.len() as f64).sqrt() as usize;
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index > sqrt {
                break;
            }
            if self._sieve[index] {
                self.rule_out(index);
            }
            index += i;
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self { _sieve: sieve };
        s.init();
        s
    }
    fn is_prime(&self, n: u32) -> bool {
        assert!(n < self._sieve.len() as u32);
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        self._sieve[n as usize]
    }
    fn primes(&self, below: u32) -> Vec<u32> {
        let mut primes: Vec<u32> = vec![2u32, 3u32];
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index >= below as usize {
                break;
            }
            if self._sieve[index] {
                primes.push(index as u32);
            }
            index += i;
        }
        primes
    }
}

fn is_circular_prime(mut p: u32, sieve: &Sieve) -> bool {
    let log10 = (p as f32).log10();
    let exp10 = 10u32.pow(log10 as u32);
    for _ in 0..log10 as u8 {
        let d = p % 10;
        p /= 10;
        p += exp10 * d;
        if !sieve.is_prime(p) {
            return false;
        }
    }
    true
}

fn main() {
    let sieve = Sieve::new(1_000_000);
    let count = sieve
        .primes(1_000_000)
        .iter()
        .filter(|&p| is_circular_prime(*p, &sieve))
        .count();

    println!("{}", count);
    assert_eq!(count, 55);
}

• Q.4 Largest palindrome product

fn generate_even_and_odd_palindromes(mut n: u32) -> (u32, u32) {
    let mut ep = n.clone();
    let mut op = n.clone();
    op /= 10;
    while n > 0 {
        ep *= 10;
        op *= 10;
        ep += n % 10;
        op += n % 10;
        n /= 10;
    }
    (ep, op)
}

fn is_double_based_palindrome(a: u32) -> bool {
    if a % 2 == 0 {
        return false;
    }
    let mut t = a.clone();
    let mut b = 0u32;
    while t > 0 {
        b <<= 1;
        b |= t & 1;
        t >>= 1;
    }
    a == b
}

fn main() {
    let mut sum = 0u32;
    let half = 10u32.pow(1_000_000f32.log10() as u32 / 2);
    for n in 1..half {
        let (ep, op) = generate_even_and_odd_palindromes(n);
        if is_double_based_palindrome(ep) {
            sum += ep;
        }
        if is_double_based_palindrome(op) {
            sum += op;
        }
    }

    println!("{}", sum);
    assert_eq!(sum, 872187);
}

fn is_palindrome(a: u32) -> bool {
    if a % 2 == 0 && a % 11 != 0 {
        return false;
    }
    let mut t = a.clone();
    let mut b = 0u32;
    while t > 0 {
        b *= 10;
        b += t % 10;
        t /= 10;
    }
    a == b
}

fn is_double_based_palindrome(a: u32) -> bool {
    if a % 2 == 0 {
        return false;
    }
    let mut t = a.clone();
    let mut b = 0u32;
    while t > 0 {
        b <<= 1;
        b |= t & 1;
        t >>= 1;
    }
    a == b
}

fn main() {
    let sum = (1..1_000_000)
        .step_by(2)
        .filter(|&n| is_palindrome(n))
        .filter(|&n| is_double_based_palindrome(n))
        .sum::<u32>();

    println!("{}", sum);
    assert_eq!(sum, 872187);
}

• A020994 Primes that are both left-truncatable and right-truncatable.
• Q.36 Double-base palindromes

fn is_prime(n: u32) -> bool {
    if n < 2 {
        return false;
    }
    if n == 2 || n == 3 || n == 5 {
        return true;
    }
    for d in &[2u32, 3, 5] {
        if n % *d == 0 {
            return false;
        }
    }
    let side = (n as f32).sqrt() as u32;
    let mut d = 5u32;
    for i in [2u32, 4].iter().cycle() {
        d += *i;
        if d > side {
            break;
        }
        if n % d == 0 {
            return false;
        }
    }
    true
}

fn generate_right_truncatable_maybe_prime_numbers(mut p: u32) -> (u32, u32, u32, u32) {
    p *= 10;
    (p + 1, p + 3, p + 7, p + 9)
}

fn is_left_trancatable_prime(p: u32) -> bool {
    let mut d = 10u32;
    while d < p {
        if !is_prime(p % d) {
            return false;
        }
        d *= 10;
    }
    true
}

fn expand_right_truncatable_prime(p: u32, left_truncatable_prime_sum: &mut u32) {
    if is_left_trancatable_prime(p) {
        *left_truncatable_prime_sum += p;
    }
    let (n1, n2, n3, n4) = generate_right_truncatable_maybe_prime_numbers(p);
    for &p in [n1, n2, n3, n4].iter().filter(|&n| is_prime(*n)) {
        expand_right_truncatable_prime(p, left_truncatable_prime_sum);
    }
}

fn main() {
    let mut left_truncatable_prime_sum = 0u32;
    for &p in [2u32, 3, 5, 7].iter() {
        expand_right_truncatable_prime(p, &mut left_truncatable_prime_sum);
    }

    println!("{}", left_truncatable_prime_sum - 2 - 3 - 5 - 7);
    assert_eq!(left_truncatable_prime_sum - 2 - 3 - 5 - 7, 748317);
}

• Q.7 10001st prime

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

struct Sieve {
    _sieve: Vec<bool>,
    _primes: Vec<usize>,
    _index: Index,
    _queue: std::collections::VecDeque<usize>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn rule_out_from_previous_position(&mut self, prime: usize, pp: usize) {
        use std::cmp::max;
        let begin = max((((pp - 1) / prime) + 1) * prime, prime * prime);
        for i in (begin..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn clean_sieve(&mut self) {
        let sqrt = ((self._sieve.len() - 1) as f32).sqrt() as usize;
        while self._index.i <= sqrt {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
                self._queue.push_back(self._index.i);
                self.rule_out(self._index.i);
            }
            self._index.increment();
        }
        while self._index.i < self._sieve.len() {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
                self._queue.push_back(self._index.i);
            }
            self._index.increment();
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self {
            _sieve: sieve,
            _primes: vec![],
            _index: Index::new(),
            _queue: std::collections::VecDeque::new(),
        };
        s._queue.push_back(2);
        s._queue.push_back(3);
        s.clean_sieve();
        s
    }
    fn extend(&mut self) {
        let previous_len = self._sieve.len();
        self._sieve.extend(vec![true; previous_len]);
        for &p in &self._primes.clone() {
            self.rule_out_from_previous_position(p, previous_len);
        }
        self.clean_sieve();
    }
    fn is_prime(&mut self, n: u32) -> bool {
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        while n > self._sieve.len() as u32 - 1 {
            self.extend();
        }
        self._sieve[n as usize]
    }
    fn next_prime(&mut self) -> u32 {
        loop {
            if let Some(p) = self._queue.pop_front() {
                return p as u32;
            }
            self.extend();
        }
    }
    fn is_left_trancatable_prime(&mut self, p: u32) -> bool {
        let mut d = 10u32;
        while d < p {
            if !self.is_prime(p % d) {
                return false;
            }
            d *= 10;
        }
        true
    }
    fn is_right_trancatable_prime(&mut self, p: u32) -> bool {
        let mut d = 10u32;
        while d < p {
            if !self.is_prime(p / d) {
                return false;
            }
            d *= 10;
        }
        true
    }
}

fn main() {
    let mut sum = 0u32;
    let mut sieve = Sieve::new(10_000);
    let mut count = 0u8;
    while count < 15 {
        let p = sieve.next_prime();
        if !sieve.is_left_trancatable_prime(p) {
            continue;
        }
        if !sieve.is_right_trancatable_prime(p) {
            continue;
        }
        count += 1;
        sum += p;
    }

    println!("{}", sum - 2 - 3 - 5 - 7);
    assert_eq!(sum - 2 - 3 - 5 - 7, 748317);
}

• Q.32 Pandigital products

fn is_pandigital(a: u32, b: u32) -> bool {
    let mut bits = 0u16;
    for n in [a, b].iter_mut() {
        while *n > 0 {
            let d = *n % 10;
            *n /= 10;
            bits |= 1 << d;
        }
    }
    bits == 0b1111111110u16
}

fn largest_pandigital_concatenated_product() -> u32 {
    for n in (9183..=(19000 / 2) as u32).rev() {
        if is_pandigital(n, n * 2) {
            return n * 100_000 + 2 * n;
        }
    }
    918_273_645
}

fn main() {
    let max = largest_pandigital_concatenated_product();

    println!("{}", max);
    assert_eq!(max, 932718654);
}

• Q.9 Special Pythagorean triplet

fn gcd(mut a: usize, mut b: usize) -> usize {
    assert!(a != 0 && b != 0);
    while b != 0 {
        let r = a % b;
        a = b;
        b = r;
    }
    a
}

fn main() {
    let mut counts = [0u8; 1001];
    for p in (12..=1000).step_by(2) {
        for m in 2..=(((p - 2) / 2) as f32).sqrt() as usize {
            for n in ((if m % 2 == 0 { 1 } else { 2 })..m).step_by(2) {
                let a = m * m - n * n;
                let b = 2 * m * n;
                let c = m * m + n * n;
                if a + b + c == p && gcd(m, n) == 1 {
                    for k in (p..=1000).step_by(p) {
                        counts[k] += 1;
                    }
                }
            }
        }
    }
    let (p, _) = counts
        .iter()
        .enumerate()
        .reduce(|(ap, a), (bp, b)| if *a > *b { (ap, a) } else { (bp, b) })
        .unwrap();

    println!("{}", p);
    assert_eq!(p, 840);
}

fn main() {
    let mut counts = [0u8; 1001];
    for c in 3..=997 {
        let mut b = 2;
        while b < 1000 - c && b < c {
            let mut a = 1;
            while a <= 1000 - c - b && a < b {
                if c * c == b * b + a * a {
                    counts[c + b + a] += 1;
                }
                a += 1;
            }
            b += 1;
        }
    }
    let (p, _) = counts
        .iter()
        .enumerate()
        .reduce(|(ap, a), (bp, b)| if *a > *b { (ap, a) } else { (bp, b) })
        .unwrap();

    println!("{}", p);
    assert_eq!(p, 840);
}

struct Container {
    capacity: u32,
    elements: u32,
}

fn digit_at(nth: u32) -> u8 {
    let mut container = Container {
        capacity: 0,
        elements: 0,
    };
    let mut w = 1u32;
    loop {
        let elements = 10u32.pow(w) - 10u32.pow(w - 1);
        let capacity = w * elements;
        if nth < container.capacity + capacity {
            break;
        }
        container.capacity += capacity;
        container.elements += elements;
        w += 1;
    }
    let residue = nth - container.capacity;
    if residue % w == 0 {
        return ((container.elements + residue / w) % 10) as u8;
    }
    let num = container.elements + residue / w + 1;
    ((num / 10u32.pow(w - residue % w)) % 10) as u8
}

fn main() {
    let p = (0u32..=6)
        .map(|d| 10u32.pow(d))
        .map(|d| digit_at(d))
        .map(|d| d as u32)
        .product::<u32>();

    println!("{}", p);
    assert_eq!(p, 210);

    assert_eq!(digit_at(1), 1);
    assert_eq!(digit_at(9), 9);
    assert_eq!(digit_at(17), 3);
    assert_eq!(digit_at(18), 1);
    assert_eq!(digit_at(189), 9);
    assert_eq!(digit_at(190), 1);
    assert_eq!(digit_at(194), 0);
    assert_eq!(digit_at(37371), 6);
}

fn consume(usable_items: &Vec<u32>, accumulated_num: u32, drain: &mut Vec<u32>) {
    if usable_items.len() == 0 {
        drain.push(accumulated_num);
        return;
    }
    for i in 0..usable_items.len() {
        let mut items = usable_items.clone();
        let mut num = accumulated_num.clone();
        let n = items.remove(i);
        num *= 10;
        num += n;
        consume(&items, num, drain);
    }
}

fn permutations(n: u32) -> Vec<u32> {
    let items = (1..=n).into_iter().rev().collect::<Vec<u32>>();
    let capacity = items.iter().map(|&i| i).product::<u32>() as usize;
    let mut drain = Vec::with_capacity(capacity);
    consume(&items, 0, &mut drain);
    drain
}

fn is_prime(n: u32) -> bool {
    if n < 2 {
        return false;
    }
    if n == 2 || n == 3 || n == 5 {
        return true;
    }
    for d in &[2u32, 3, 5] {
        if n % *d == 0 {
            return false;
        }
    }
    let side = (n as f32).sqrt() as u32;
    let mut d = 5u32;
    for i in [2u32, 4].iter().cycle() {
        d += *i;
        if d > side {
            break;
        }
        if n % d == 0 {
            return false;
        }
    }
    true
}

fn main() {
    let mut p = None;
    'exploration: for &d in [7, 4].iter() {
        for n in permutations(d) {
            if is_prime(n) {
                p = Some(n);
                break 'exploration;
            }
        }
    }

    println!("{:?}", p);
    assert_eq!(p, Some(7652413));
}

• Q.12 Highly divisible triangular number
• Q.8 Largest product in a series

Because the original word list is very long, this example has only a part of it.

fn is_triangle_number(x: u32) -> bool {
    let expr = 8 * x + 1;
    let side = (expr as f64).sqrt() as u32;
    side * side == expr
}

fn word_value(w: &str) -> u32 {
    w.chars().map(|c| c as u32 - 'A' as u32 + 1).sum::<u32>()
}

fn main() {
    let count = WORDS
        .iter()
        .map(|&w| word_value(w))
        .filter(|&v| is_triangle_number(v))
        .count();

    println!("{:?}", count);
    assert_eq!(count, 5);
}

const WORDS: &[&str] = &[
    "A",
    "ABILITY",
    "ABLE",
    "ABOUT",
    "ABOVE",
    "ABSENCE",
    "ABSOLUTELY",
    "ACADEMIC",
    "ACCEPT",
    "ACCESS",
    "ACCIDENT",
    "ACCOMPANY",
    "ACCORDING",
    "ACCOUNT",
    "ACHIEVE",
    "ACHIEVEMENT",
    "ACID"
];

• Q.41 Pandigital prime

fn is_divisible(n: u64, depth: u8) -> bool {
    if depth < 2 || depth == 9 {
        return true;
    }
    let p = match depth {
        2 => 17,
        3 => 13,
        4 => 11,
        5 => 7,
        6 => 5,
        7 => 3,
        8 => 2,
        _ => unreachable!(),
    };
    (n / 10u64.pow(depth as u32 - 2)) % p == 0
}

fn consume(
    usable_items: &Vec<u8>,
    accumulated_num: u64,
    drain: &mut Vec<u64>,
    depth: u8,
) {
    if usable_items.len() == 0 {
        drain.push(accumulated_num);
        return;
    }
    for i in 0..usable_items.len() {
        let mut items = usable_items.clone();
        let mut num = accumulated_num.clone();
        let n = items.remove(i);
        let weight = 10u64.pow(depth as u32);
        num += weight * n as u64;
        if !is_divisible(num, depth) {
            continue;
        }
        consume(&items, num, drain, depth + 1);
    }
}

fn permutations_with_conditions() -> Vec<u64> {
    let items = (0..=9).into_iter().collect::<Vec<u8>>();
    let mut drain = vec![];
    consume(&items, 0, &mut drain, 0);
    drain
}

fn main() {
    let sum = permutations_with_conditions()
        .iter()
        .filter(|&n| *n > 999_999_999)
        .sum::<u64>();

    println!("{}", sum);
    assert_eq!(sum, 16695334890);
}

fn is_divisible(n: u64, depth: u8) -> bool {
    if depth < 3 {
        return true;
    }
    let p = match depth {
        3 => 2,
        4 => 3,
        5 => 5,
        6 => 7,
        7 => 11,
        8 => 13,
        9 => 17,
        _ => unreachable!(),
    };
    (n % 1000) % p == 0
}

fn consume(
    usable_items: &Vec<u8>,
    accumulated_num: u64,
    drain: &mut Vec<u64>,
    depth: u8,
) {
    if usable_items.len() == 0 {
        drain.push(accumulated_num);
        return;
    }
    for i in 0..usable_items.len() {
        let mut items = usable_items.clone();
        let mut num = accumulated_num.clone();
        let n = items.remove(i);
        num *= 10;
        num += n as u64;
        if !is_divisible(num, depth) {
            continue;
        }
        consume(&items, num, drain, depth + 1);
    }
}

fn permutations_with_conditions() -> Vec<u64> {
    let items = (0..=9).into_iter().collect::<Vec<u8>>();
    let mut drain = vec![];
    consume(&items, 0, &mut drain, 0);
    drain
}

fn main() {
    let sum = permutations_with_conditions()
        .iter()
        .filter(|&n| *n > 999_999_999)
        .sum::<u64>();

    println!("{}", sum);
    assert_eq!(sum, 16695334890);
}

• Q.42 Coded triangle numbers

fn is_pentagonal(n: u64) -> bool {
    let expr = 24 * n + 1;
    let sqrt = (expr as f64).sqrt() as u64;
    if expr != sqrt * sqrt {
        return false;
    }
    sqrt % 6 == 5
}

fn pentagon(n: u64) -> u64 {
    n * (3 * n - 1) / 2
}

fn calc_distance(pentagons: &mut Vec<u64>) -> (u64, u64) {
    for n in 1u64.. {
        let p1 = pentagon(n);
        for &p2 in pentagons.iter().rev() {
            let d = p1 - p2;
            let s = p1 + p2;
            if is_pentagonal(d) && is_pentagonal(s) {
                return (d, n);
            }
        }
        pentagons.push(p1);
    }
    unreachable!("This function is supposed to have return but not break in the outermost loop!");
}

fn is_answer_confirmed(pentagons: &mut Vec<u64>, distance: u64, nth: u64) -> bool {
    pentagons.push(pentagon(nth));
    for n in nth + 1.. {
        let p1 = pentagon(n);
        if 3 * (n - 1) + 1 > distance {
            return true;
        }
        for &p2 in pentagons.iter().rev() {
            let d = p1 - p2;
            if d >= distance {
                break;
            }
            let s = p1 + p2;
            if is_pentagonal(d) && is_pentagonal(s) {
                return false;
            }
        }
        pentagons.push(p1);
    }
    unreachable!("This function is supposed to have return but not break in the outermost loop!");
}

fn main() {
    let mut pentagons = vec![];
    let (d, nth) = calc_distance(&mut pentagons);
    assert!(is_answer_confirmed(&mut pentagons, d, nth));

    println!("{}", d);
    assert_eq!(d, 5482660);
}

struct Pentagon {
    n: u64,
    v: u64,
}

impl Pentagon {
    fn increment(&mut self) {
        self.v += self.n * 3 + 1;
        self.n += 1;
    }
    fn value(&self) -> u64 {
        self.v
    }
}

struct Hexagon {
    n: u64,
    v: u64,
}

impl Hexagon {
    fn increment(&mut self) {
        self.v += 4 * self.n + 1;
        self.n += 1;
    }
    fn value(&self) -> u64 {
        self.v
    }
}

fn main() {
    let mut p = Pentagon { n: 165, v: 40755 };
    let mut h = Hexagon { n: 143, v: 40755 };
    p.increment();
    let v = loop {
        while p.value() < h.value() {
            p.increment();
        }
        while h.value() < p.value() {
            h.increment();
        }
        if p.value() == h.value() {
            break p.value();
        }
    };

    println!("{}", v);
    assert_eq!(v, 1533776805);
}

• Q.37 Truncatable primes

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

struct Sieve {
    _sieve: Vec<bool>,
    _primes: Vec<usize>,
    _index: Index,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn clean_sieve(&mut self) {
        let sqrt = (self._sieve.len() as f32).sqrt() as usize;
        while self._index.i <= sqrt {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
                self.rule_out(self._index.i);
            }
            self._index.increment();
        }
        while self._index.i < self._sieve.len() {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
            }
            self._index.increment();
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self {
            _sieve: sieve,
            _primes: vec![],
            _index: Index::new(),
        };
        s.clean_sieve();
        s
    }
    fn extend(&mut self) {
        self._sieve.extend(vec![true; self._sieve.len()]);
        let primes = self._primes.clone();
        for &p in primes.iter() {
            self.rule_out(p);
        }
        self.clean_sieve();
    }
    fn is_prime(&mut self, n: u32) -> bool {
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        while n > self._sieve.len() as u32 - 1 {
            self.extend();
        }
        self._sieve[n as usize]
    }
}

struct DoubleSquares {
    _n: u32,
    _elements: Vec<u32>,
}

impl DoubleSquares {
    fn new() -> Self {
        Self {
            _n: 5,
            _elements: vec![2, 8, 18, 32, 50],
        }
    }
    fn extend(&mut self) {
        for n in self._n + 1..self._n * 2 {
            self._elements.push(n * n * 2);
        }
        self._n *= 2;
    }
    fn double_check(&mut self, sieve: &mut Sieve, o: u32) -> Result<(), ()> {
        while o > self._elements.last().map(|&n| n).unwrap_or(0) {
            self.extend();
        }
        for &d in &self._elements {
            if d >= o {
                return Err(());
            }
            if sieve.is_prime(o - d) {
                return Ok(());
            }
        }
        panic!("This function is supposed to have return but not break in loop!");
    }
}

fn explore_error_value() -> u32 {
    let mut sieve = Sieve::new(1000);
    let mut double_squares = DoubleSquares::new();
    for o in (9..).step_by(2) {
        if sieve.is_prime(o) {
            continue;
        }
        if double_squares.double_check(&mut sieve, o).is_err() {
            return o;
        }
    }
    unreachable!("This function is supposed to have return but not break in loop!");
}

fn main() {
    let e = explore_error_value();
    println!("{}", e);
    assert_eq!(e, 5777);
}

• Q.37 Truncatable primes

struct Sieve {
    _sieve: Vec<bool>,
    _count: Vec<u8>,
    _primes: Vec<usize>,
    _cursor: usize,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
            self._count[i] += 1;
        }
    }
    fn rule_out_from_previous_position(&mut self, prime: usize, pp: usize) {
        let begin = (((pp - 1) / prime) + 1) * prime;
        for i in (begin..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
            self._count[i] += 1;
        }
    }
    fn is_start_of_four_consective_nums_with_factors(&self) -> bool {
        let i = self._cursor;
        if self._count[i] != 4 {
            return false;
        }
        if self._count.len() - 1 < i + 3 {
            return false;
        }
        self._count[i + 1] == 4 && self._count[i + 2] == 4 && self._count[i + 3] == 4
    }
    fn clean_sieve_with_exploration(&mut self) -> Option<u32> {
        while self._cursor < self._sieve.len() {
            if self._sieve[self._cursor] {
                self._primes.push(self._cursor);
                self.rule_out(self._cursor);
                continue;
            }
            if self.is_start_of_four_consective_nums_with_factors() {
                return Some(self._cursor as u32);
            }
            self._cursor += 1;
        }
        None
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let count = vec![0u8; below as usize];
        Self {
            _sieve: sieve,
            _count: count,
            _primes: vec![],
            _cursor: 2,
        }
    }
    fn extend(&mut self) {
        let prev_len = self._sieve.len();
        self._sieve.extend(vec![true; self._sieve.len()]);
        self._count.extend(vec![0u8; self._count.len()]);
        let primes = self._primes.clone();
        for &p in primes.iter() {
            self.rule_out_from_previous_position(p, prev_len);
        }
    }
}

fn main() {
    let mut sieve = Sieve::new(10_000);
    let n = loop {
        if let Some(n) = sieve.clean_sieve_with_exploration() {
            break n;
        }
        sieve.extend();
    };

    println!("{}", n);
    assert_eq!(n, 134043);
}

• Q.2 Even Fibonacci numbers
• Q.26 Reciprocal cycles
• Binary Exponentiation - CP-Algorithms

fn conservative_mod_pow(a: u64, exp: u64, m: u64) -> u64 {
    let mut result = 1;
    for _ in 0..exp {
        result *= a;
        result %= m;
    }
    result
}

fn main() {
    let m = 10_000_000_000;
    let mut sum = 0u64;
    for n in 1..=1000 {
        sum += conservative_mod_pow(n, n, m);
        sum %= m;
    }

    println!("{}", sum);
    assert_eq!(sum, 9110846700);
}

fn mod_pow(a: u64, exp: u64, m: u64) -> u64 {
    let (mut a, mut exp, m) = (a as u128, exp as u128, m as u128);
    if m == 1 {
        return 0;
    }
    if exp == 0 {
        return 1;
    }
    let mut result = 1;
    a %= m;
    loop {
        if exp % 2 == 1 {
            result *= a;
            result %= m;
        }
        exp >>= 1;
        if exp == 0 {
            break;
        }
        a *= a;
        a %= m;
    }
    result as u64
}

fn main() {
    let m = 10_000_000_000u64;
    let mut sum = 0u64;
    for n in 1..=1000 {
        sum += mod_pow(n, n, m);
        sum %= m;
    }

    println!("{}", sum);
    assert_eq!(sum, 9110846700);
}

• Q.38 Pandigital multiples

struct Sieve {
    _sieve: Vec<bool>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn init(&mut self) {
        let sqrt = (self._sieve.len() as f64).sqrt() as usize;
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index > sqrt {
                break;
            }
            if self._sieve[index] {
                self.rule_out(index);
            }
            index += i;
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self { _sieve: sieve };
        s.init();
        s
    }
    fn is_prime(&self, n: u32) -> bool {
        assert!(n < self._sieve.len() as u32);
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        self._sieve[n as usize]
    }
    fn primes(&self, below: u32) -> Vec<u32> {
        let mut primes: Vec<u32> = vec![2u32, 3u32];
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index >= below as usize {
                break;
            }
            if self._sieve[index] {
                primes.push(index as u32);
            }
            index += i;
        }
        primes
    }
}

fn is_permutations(mut a: u32, mut b: u32, mut c: u32) -> bool {
    assert!(a > 999 && b > 999 && c > 999);
    assert!(a < 10000 && b < 10000 && c < 10000);
    for n in [&mut a, &mut b, &mut c].iter_mut() {
        **n *= 10;
        **n += 1;
    }
    let (mut a_bits, mut b_bits, mut c_bits) = (0u16, 0u16, 0u16);
    for (n, bits) in [
        (&mut a, &mut a_bits),
        (&mut b, &mut b_bits),
        (&mut c, &mut c_bits),
    ]
    .iter_mut()
    {
        while **n > 1 {
            let d = **n % 10;
            **n /= 10;
            **bits |= 1 << d;
        }
    }
    a_bits == b_bits && b_bits == c_bits
}

fn main() {
    let sieve = Sieve::new(10_000);
    let series = sieve
        .primes(10_000)
        .iter()
        .filter(|&p| *p > 999 && *p < 10_000 - 6660)
        .filter(|&p| sieve.is_prime(*p + 3330) && sieve.is_prime(*p + 6660))
        .filter(|&p| *p != 1487)
        .filter(|&p| is_permutations(*p, *p + 3330, *p + 6660))
        .map(|&p| p as u64)
        .map(|p| p * 100_000_000 + (p + 3330) * 10_000 + p + 6660)
        .last()
        .expect("The prime series with a difference of 3330 not found!");

    println!("{}", series);
    assert_eq!(series, 296962999629);
}

• Q.7 10001st prime
• Q.26 Reciprocal cycles

fn mod_pow(a: u32, exp: u32, m: u32) -> u32 {
    let (mut a, mut exp, m) = (a as u64, exp as u64, m as u64);
    if m == 1 {
        return 0;
    }
    if exp == 0 {
        return 1;
    }
    let mut result = 1;
    a %= m;
    loop {
        if exp % 2 == 1 {
            result *= a;
            result %= m;
        }
        exp >>= 1;
        if exp == 0 {
            break;
        }
        a *= a;
        a %= m;
    }
    result as u32
}

fn gcd(mut a: u32, mut b: u32) -> u32 {
    assert!(a != 0 && b != 0);
    while b != 0 {
        let r = a % b;
        a = b;
        b = r;
    }
    a
}

fn pseudo_fermat_test(n: u32) -> bool {
    gcd(223092870, n) == 1 && mod_pow(223092870, n - 1, n) == 1
}

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn rule_out_from_previous_position(sieve: &mut Vec<bool>, prime: usize, pp: usize) {
    use std::cmp::max;
    let begin = max((((pp - 1) / prime) + 1) * prime, prime * prime);
    for i in (begin..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn extend(sieve: &mut Vec<bool>, primes: &Vec<usize>) {
    let previous_len = sieve.len();
    sieve.extend(vec![true; previous_len]);
    for &p in primes {
        rule_out_from_previous_position(sieve, p, previous_len);
    }
}

fn main() {
    let mut sum = 2u32 + 3;
    let mut sieve = vec![true; 1000];
    let mut primes: Vec<usize> = vec![];
    let mut cursor = 5usize;
    let mut ite = [2usize, 4].iter().cycle();
    'sum_fill: loop {
        while cursor < sieve.len() {
            if !sieve[cursor] {
                cursor += ite.next().unwrap();
                continue;
            }
            &primes.push(cursor);
            rule_out(&mut sieve, cursor);
            sum += cursor as u32;
            if sum >= 1_000_000 {
                sum -= cursor as u32;
                break 'sum_fill;
            }
            cursor += ite.next().unwrap();
        }
        extend(&mut sieve, &primes);
    }

    primes.insert(0, 2);
    primes.insert(1, 3);
    for p in primes {
        sum -= p as u32;
        if pseudo_fermat_test(sum) {
            break;
        }
    }

    println!("{}", sum);
    assert_eq!(sum, 997651);
}

• Fermat primality test, khanacademy
• List of Carmichael numbers

• Q.58 Spiral primes

struct Sieve {
    _sieve: Vec<bool>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn init(&mut self) {
        let sqrt = (self._sieve.len() as f64).sqrt() as usize;
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index > sqrt {
                break;
            }
            if self._sieve[index] {
                self.rule_out(index);
            }
            index += i;
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self { _sieve: sieve };
        s.init();
        s
    }
    fn is_prime(&self, n: u32) -> bool {
        assert!(n < self._sieve.len() as u32);
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        self._sieve[n as usize]
    }
    fn primes(&self, below: u32) -> Vec<u32> {
        let mut primes = vec![2u32, 3u32];
        let mut index = 5usize;
        for &i in [2usize, 4].iter().cycle() {
            if index >= below as usize {
                break;
            }
            if self._sieve[index] {
                primes.push(index as u32);
            }
            index += i;
        }
        primes
    }
}

fn fill_sum_up_to_million(primes: &[u32]) -> u32 {
    let mut sum = 0u32;
    for &p in primes {
        sum += p;
        if sum > 1_000_000 {
            sum -= p;
            return sum;
        }
    }
    panic!("The prime list was not enough to fill up the sum to be 1 million!");
}

fn main() {
    let sieve = Sieve::new(1_000_000);
    let primes = sieve.primes(1_000_000);
    let mut sum = fill_sum_up_to_million(&primes);
    for p in primes {
        sum -= p;
        if sieve.is_prime(sum) {
            break;
        }
    }

    println!("{}", sum);
    assert_eq!(sum, 997651);
}

• Q.37 Truncatable primes

struct Index {
    i: usize,
    _ite: Box<dyn Iterator<Item = usize>>,
}

impl Index {
    fn increment(&mut self) {
        self.i += self._ite.next().unwrap();
    }
    fn new() -> Self {
        Self {
            i: 5,
            _ite: Box::new(vec![2usize, 4].into_iter().cycle()),
        }
    }
}

struct Sieve {
    _sieve: Vec<bool>,
    _primes: Vec<usize>,
    _index: Index,
    _queue: std::collections::VecDeque<usize>,
}

impl Sieve {
    fn rule_out(&mut self, prime: usize) {
        for i in (prime * prime..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn rule_out_from_previous_position(&mut self, prime: usize, pp: usize) {
        use std::cmp::max;
        let begin = max((((pp - 1) / prime) + 1) * prime, prime * prime);
        for i in (begin..self._sieve.len()).step_by(prime) {
            self._sieve[i] = false;
        }
    }
    fn clean_sieve(&mut self) {
        let sqrt = (self._sieve.len() as f32).sqrt() as usize;
        while self._index.i <= sqrt {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
                self._queue.push_back(self._index.i);
                self.rule_out(self._index.i);
            }
            self._index.increment();
        }
        while self._index.i < self._sieve.len() {
            if self._sieve[self._index.i] {
                self._primes.push(self._index.i);
                self._queue.push_back(self._index.i);
            }
            self._index.increment();
        }
    }
    fn new(below: u32) -> Self {
        assert!(below > 4);
        let sieve = vec![true; below as usize];
        let mut s = Self {
            _sieve: sieve,
            _primes: vec![],
            _index: Index::new(),
            _queue: std::collections::VecDeque::new(),
        };
        s._queue.push_back(2);
        s._queue.push_back(3);
        s.clean_sieve();
        s
    }
    fn extend(&mut self) {
        let previous_len = self._sieve.len();
        self._sieve.extend(vec![true; previous_len]);
        for &p in &self._primes.clone() {
            self.rule_out_from_previous_position(p, previous_len);
        }
        self.clean_sieve();
    }
    fn is_prime(&mut self, n: u32) -> bool {
        if n == 2 || n == 3 {
            return true;
        }
        if n == 0 || n == 1 || n % 2 == 0 || n % 3 == 0 {
            return false;
        }
        while n > self._sieve.len() as u32 - 1 {
            self.extend();
        }
        self._sieve[n as usize]
    }
    fn next_prime(&mut self) -> u32 {
        loop {
            if let Some(p) = self._queue.pop_front() {
                return p as u32;
            }
            self.extend();
        }
    }
}

fn appearance_frequency_excluding_tail(mut p: u32, frequency: &mut Frequency) {
    frequency.clear();
    p /= 10;
    while p > 0 {
        let d = p % 10;
        frequency.0[d as usize] += 1;
        p /= 10;
    }
}

fn expand_wildcard(mut p: u32, wildcard: u8, expansion: &mut WildcardExpansion) {
    expansion.clear();
    let mut dicimal_place = 1u32;
    let first_digit = p % 10;
    for n in &mut expansion.0 {
        *n += first_digit;
    }
    p /= 10;
    while p > 0 {
        dicimal_place *= 10;
        let d = (p % 10) as u8;
        let is_wildcard = d as u8 == wildcard;
        for (i, n) in expansion.0.iter_mut().enumerate() {
            *n += dicimal_place * if is_wildcard { i as u32 } else { d as u32 };
        }
        p /= 10;
    }
}

fn digit_len_match(mut a: u32, mut b: u32) -> bool {
    while a > 0 && b > 0 {
        a /= 10;
        b /= 10;
    }
    a == b
}

struct Frequency([u8; 10]);
impl Frequency {
    const BLANK: [u8; 10] = [0u8; 10];
    fn clear(&mut self) {
        self.0.copy_from_slice(&Self::BLANK[..]);
    }
    fn new() -> Self {
        Frequency(Frequency::BLANK.clone())
    }
}

struct WildcardExpansion([u32; 10]);
impl WildcardExpansion {
    const BLANK: [u32; 10] = [0u32; 10];
    fn clear(&mut self) {
        self.0.copy_from_slice(&Self::BLANK[..]);
    }
    fn new() -> Self {
        WildcardExpansion(WildcardExpansion::BLANK.clone())
    }
}

fn smallest_prime_with_repetition_of_family(replacement: u8, family_length: u8) -> u32 {
    assert!(family_length > 4);
    let mut sieve = Sieve::new(10_000);
    let mut p = sieve.next_prime();
    while p < 10 {
        p = sieve.next_prime();
    }

    let mut frequency = Frequency::new();
    let mut expansion = WildcardExpansion::new();
    'explorarion: loop {
        appearance_frequency_excluding_tail(p, &mut frequency);
        for (i, _) in frequency
            .0
            .iter()
            .enumerate()
            .filter(|(_, &f)| f == replacement)
        {
            expand_wildcard(p, i as u8, &mut expansion);
            let mut family = expansion.0[1..]
                .iter()
                .map(|&n| n)
                .filter(|&n| sieve.is_prime(n))
                .collect::<Vec<u32>>();
            if sieve.is_prime(expansion.0[0]) && digit_len_match(expansion.0[0], p) {
                family.insert(0, expansion.0[0]);
            }
            if family.len() as u8 == family_length {
                println!("{:?}", &family);
                break 'explorarion family[0];
            }
        }
        p = sieve.next_prime();
    }
}

fn main() {
    {
        let p = smallest_prime_with_repetition_of_family(1, 6);
        assert_eq!(p, 13);
    }
    {
        let p = smallest_prime_with_repetition_of_family(2, 7);
        assert_eq!(p, 56003);
    }
    {
        let p = smallest_prime_with_repetition_of_family(3, 8);
        assert_eq!(p, 121313);
    }
    {
        // timeout with playground
        // https://www.hackerrank.com/contests/projecteuler/challenges/euler051/forum/comments/310849
        // let p = smallest_prime_with_repetition_of_family(4, 6);
        // assert_eq!(p, 2422027);
    }
    {
        // timeout with playground
        // https://www.hackerrank.com/contests/projecteuler/challenges/euler051/forum/comments/592444
        // let p = smallest_prime_with_repetition_of_family(4, 7);
        // assert_eq!(p, 80047003);
    }
    {
        // timeout with playground
        // https://projecteuler.net/action=quote;post_id=382609
        // let p = smallest_prime_with_repetition_of_family(3, 9);
        // assert_eq!(p, 38000201);
    }
}

• Q.26 Reciprocal cycles

const BLANK: [u8; 10] = [0u8; 10];

fn histogram(mut n: u32, digits: &mut [u8; 10]) {
    digits.copy_from_slice(&BLANK);
    while n > 0 {
        let d = (n % 10) as usize;
        digits[d] += 1;
        n /= 10;
    }
}

fn explorarion(place: u32, digit_matrix: &mut [[u8; 10]; 6]) -> Option<u32> {
    'next_x: for x in place..place * 10 / 6 {
        histogram(x, &mut digit_matrix[0]);
        for a in 2usize..=6 {
            histogram(a as u32 * x, &mut digit_matrix[a - 1]);
            if digit_matrix[0] != digit_matrix[a - 1] {
                continue 'next_x;
            }
        }
        return Some(x);
    }
    None
}

fn main() {
    let mut digit_matrix = [[0u8; 10]; 6];
    let mut place = 100u32;
    let n = loop {
        match explorarion(place, &mut digit_matrix) {
            Some(n) => break n,
            None => place *= 10,
        }
    };
    println!("{}", n);
    assert_eq!(n, 142857);
}

• Q.18 Maximum path sum I
• Q.15 Lattice paths

const ONE_MILLION: u32 = 1_000_000;

fn main() {
    let mut count = 0u32;
    let mut prev = [0u32; 101];
    let mut line = [0u32; 101];
    prev[0] = 1;
    for _ in 0..100 {
        line[0] = 1;
        for (i, &v) in prev.iter().enumerate() {
            if v == 0 {
                break;
            }
            let binom = v + prev[i + 1];
            line[i + 1] = if binom > ONE_MILLION {
                count += 1;
                ONE_MILLION
            } else {
                binom
            }
        }
        prev.copy_from_slice(&line);
    }

    println!("{}", count);
    assert_eq!(count, 4075);
}

use std::slice::Iter;

#[derive(Clone, PartialEq)]
enum Symbol {
    Spade,
    Diamond,
    Club,
    Heart,
}

impl Symbol {
    fn iterator() -> Iter<'static, Symbol> {
        use self::Symbol::*;
        static SYMBOLS: [Symbol; 4] = [Spade, Diamond, Club, Heart];
        SYMBOLS.iter()
    }
}

#[derive(Clone)]
struct Card {
    num: u8,
    symbol: Symbol,
}

impl Default for Card {
    fn default() -> Self {
        Card {
            num: 1,
            symbol: Symbol::Heart,
        }
    }
}

struct Game {
    hands: [[Card; 5]; 2],
    histograms: [[u8; 13]; 2],
}

impl Game {
    const BLANK: [u8; 13] = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0];
    fn new() -> Self {
        let c = Card {
            ..Default::default()
        };
        Game {
            hands: [
                [c.clone(), c.clone(), c.clone(), c.clone(), c.clone()],
                [c.clone(), c.clone(), c.clone(), c.clone(), c.clone()],
            ],
            histograms: [Self::BLANK.clone(); 2],
        }
    }
    fn load(&mut self, text: &str) {
        self.histograms[0].copy_from_slice(&Self::BLANK);
        self.histograms[1].copy_from_slice(&Self::BLANK);
        for (i, t) in text.split_ascii_whitespace().enumerate() {
            let card = &mut self.hands[i / 5][i % 5];
            card.num = match t.chars().nth(0).unwrap() {
                'A' => 1,
                '2' => 2,
                '3' => 3,
                '4' => 4,
                '5' => 5,
                '6' => 6,
                '7' => 7,
                '8' => 8,
                '9' => 9,
                'T' => 10,
                'J' => 11,
                'Q' => 12,
                'K' => 13,
                _ => unreachable!(),
            };
            self.histograms[i / 5][card.num as usize - 1] += 1;
            card.symbol = match t.chars().nth(1).unwrap() {
                'S' => Symbol::Spade,
                'D' => Symbol::Diamond,
                'C' => Symbol::Club,
                'H' => Symbol::Heart,
                _ => unreachable!(),
            };
        }
    }
    fn has_left_higher_card(&self) -> bool {
        match (self.histograms[0][0] > 0, self.histograms[1][0] > 0) {
            (true, false) => return true,
            (false, true) => return false,
            _ => (),
        }
        let l = self.hands[0].iter().map(|c| c.num).max().unwrap();
        let r = self.hands[1].iter().map(|c| c.num).max().unwrap();
        if l != r {
            return l > r;
        } else {
            unimplemented!("not only max, need to do further comparison")
        }
    }
    fn is_left_winner(&self) -> bool {
        match (
            has_royal_flush(&self.hands[0]),
            has_royal_flush(&self.hands[1]),
        ) {
            (true, false) => return true,
            (false, true) => return false,
            (false, false) => (),
            (true, true) => panic!(),
        }

        match (
            has_straight_flush(&self.hands[0]),
            has_straight_flush(&self.hands[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some(l), Some(r)) => {
                if l != r {
                    return l > r;
                } else {
                    panic!()
                }
            }
        }

        match (
            has_four_of_a_kind(&self.histograms[0]),
            has_four_of_a_kind(&self.histograms[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some((l4, l1)), Some((r4, r1))) => {
                if l4 != r4 {
                    return l4 > r4;
                } else if l1 != r1 {
                    return l1 > r1;
                } else {
                    panic!()
                }
            }
        }

        match (
            has_full_house(&self.histograms[0]),
            has_full_house(&self.histograms[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some((l3, l2)), Some((r3, r2))) => {
                if l3 != r3 {
                    return l3 > r3;
                } else if l2 != r2 {
                    return l2 > r2;
                } else {
                    panic!()
                }
            }
        }

        match (has_flush(&self.hands[0]), has_flush(&self.hands[1])) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some(l), Some(r)) => {
                if l != r {
                    return l > r;
                } else {
                    panic!()
                }
            }
        }

        match (has_straight(&self.hands[0]), has_straight(&self.hands[1])) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some(l), Some(r)) => {
                if l != r {
                    return l > r;
                } else {
                    panic!()
                }
            }
        }

        match (
            has_three_of_a_kind(&self.histograms[0]),
            has_three_of_a_kind(&self.histograms[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some((l3, lo)), Some((r3, ro))) => {
                if l3 != r3 {
                    return l3 > r3;
                } else if lo != ro {
                    return lo > ro;
                } else {
                    unimplemented!("need to compare the weakest card")
                }
            }
        }

        match (
            has_two_pairs(&self.histograms[0]),
            has_two_pairs(&self.histograms[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some((lg, ll, lo)), Some((rg, rl, ro))) => {
                if lg != rg {
                    return lg > rg;
                } else if ll != rl {
                    return ll > rl;
                } else if lo != ro {
                    return lo > ro;
                } else {
                    panic!()
                }
            }
        }

        match (
            has_one_pair(&self.histograms[0]),
            has_one_pair(&self.histograms[1]),
        ) {
            (Some(_), None) => return true,
            (None, Some(_)) => return false,
            (None, None) => (),
            (Some((l, lo)), Some((r, ro))) => {
                if l != r {
                    return l > r;
                } else if lo != ro {
                    return lo > ro;
                } else {
                    unimplemented!("need to compare the two weakest cards")
                }
            }
        }

        self.has_left_higher_card()
    }
}

fn has_royal_flush(hand: &[Card; 5]) -> bool {
    if !Symbol::iterator().any(|s| hand.iter().all(|c| c.symbol == *s)) {
        return false;
    }
    let mut bits = 0u32;
    hand.iter().for_each(|c| bits |= 1u32 << c.num);
    bits == 0b11110000000010
}

fn has_straight_flush(hand: &[Card; 5]) -> Option<u32> {
    if !Symbol::iterator().any(|s| hand.iter().all(|c| c.symbol == *s)) {
        return None;
    }
    let mut bits = 0u32;
    hand.iter().for_each(|c| bits |= 1u32 << c.num);
    let mut mask = 0b11111000000000u32;
    while mask & 0b01 == 0 {
        if bits == mask {
            return Some(bits);
        }
        mask >>= 1;
    }
    None
}

/// has_four_of_a_kind returns Option<(four, one)>
fn has_four_of_a_kind(histogram: &[u8; 13]) -> Option<(u8, u8)> {
    let (mut four, mut one) = (None, None);
    for (i, &v) in histogram.iter().enumerate() {
        match v {
            4 => four = Some(i),
            1 => one = Some(i),
            _ => (),
        }
    }
    match (four, one) {
        (Some(f), Some(o)) => Some((
            if f == 0 { u8::MAX } else { f as u8 },
            if o == 0 { u8::MAX } else { o as u8 },
        )),
        _ => None,
    }
}

/// has_full_house returns Option<(triple, pair)>
fn has_full_house(histogram: &[u8; 13]) -> Option<(u8, u8)> {
    let (mut triple, mut pair) = (None, None);
    for (i, &v) in histogram.iter().enumerate() {
        match v {
            3 => triple = Some(i),
            2 => pair = Some(i),
            _ => (),
        }
    }
    match (triple, pair) {
        (Some(t), Some(p)) => Some((
            if t == 0 { u8::MAX } else { t as u8 },
            if p == 0 { u8::MAX } else { p as u8 },
        )),
        _ => None,
    }
}

fn has_flush(hand: &[Card; 5]) -> Option<u8> {
    if !Symbol::iterator().any(|s| hand.iter().all(|c| c.symbol == *s)) {
        return None;
    }
    Some(hand.iter().map(|c| c.num).max().unwrap())
}

fn has_straight(hand: &[Card; 5]) -> Option<u32> {
    let mut bits = 0u32;
    hand.iter().for_each(|c| bits |= 1u32 << c.num);
    if bits == 0b11110000000010 {
        return Some(u32::MAX);
    }
    let mut mask = 0b11111000000000u32;
    while mask & 0b01 == 0 {
        if bits == mask {
            return Some(mask);
        }
        mask >>= 1;
    }
    None
}

/// has_three_of_a_kind returns Option<(three, max(other))>
fn has_three_of_a_kind(histogram: &[u8; 13]) -> Option<(u8, u8)> {
    let (mut triple, mut other) = (None, None);
    for (i, &v) in histogram.iter().enumerate() {
        match v {
            3 => triple = Some(i),
            n if n > 0 && i == 0 => other = Some(0),
            n if n > 0 => other = std::cmp::max(other, Some(i)),
            _ => (),
        }
    }
    match (triple, other) {
        (Some(t), Some(o)) => Some((
            if t == 0 { u8::MAX } else { t as u8 },
            if o == 0 { u8::MAX } else { o as u8 },
        )),
        _ => None,
    }
}

/// has_two_pairs returns Option<(higher, lower, other)>
fn has_two_pairs(histogram: &[u8; 13]) -> Option<(u8, u8, u8)> {
    let mut iter = histogram
        .iter()
        .enumerate()
        .filter(|(_, &c)| c == 2)
        .map(|(i, _)| if i == 0 { u8::MAX } else { i as u8 });
    let a = iter.next();
    let b = iter.next();
    match (a, b) {
        (Some(i), Some(j)) => {
            let c = histogram
                .iter()
                .enumerate()
                .filter(|(_, &c)| c == 1)
                .map(|(i, _)| if i == 0 { u8::MAX } else { i as u8 })
                .next()
                .unwrap();
            Some((std::cmp::max(i, j), std::cmp::min(i, j), c))
        }
        _ => None,
    }
}

/// has_one_pair returns Option<(pair, max(other))>
fn has_one_pair(histogram: &[u8; 13]) -> Option<(u8, u8)> {
    if histogram.iter().filter(|&c| *c == 2).count() != 1 {
        return None;
    }
    let (mut pair, mut other) = (None, None);
    for (i, &v) in histogram.iter().enumerate() {
        match v {
            2 => pair = Some(i),
            n if n > 0 && i == 0 => other = Some(0),
            n if n > 0 => other = std::cmp::max(other, Some(i)),
            _ => (),
        }
    }
    match (pair, other) {
        (Some(p), Some(o)) => Some((
            if p == 0 { u8::MAX } else { p as u8 },
            if o == 0 { u8::MAX } else { o as u8 },
        )),
        _ => None,
    }
}

fn main() {
    let mut game = Game::new();
    let mut count = 0u32;
    for source in GAMES.iter() {
        game.load(source);
        if game.is_left_winner() {
            count += 1;
        }
    }

    println!("{}", count);
    assert_eq!(count, 376);
}

const GAMES: [&str; 1000] = [
    "8C TS KC 9H 4S 7D 2S 5D 3S AC",
    "5C AD 5D AC 9C 7C 5H 8D TD KS",
    "3H 7H 6S KC JS QH TD JC 2D 8S",
    "TH 8H 5C QS TC 9H 4D JC KS JS",
    "7C 5H KC QH JD AS KH 4C AD 4S",
    "5H KS 9C 7D 9H 8D 3S 5D 5C AH",
    "6H 4H 5C 3H 2H 3S QH 5S 6S AS",
    "TD 8C 4H 7C TC KC 4C 3H 7S KS",
    "7C 9C 6D KD 3H 4C QS QC AC KH",
    "JC 6S 5H 2H 2D KD 9D 7C AS JS",
    "AD QH TH 9D 8H TS 6D 3S AS AC",
    "2H 4S 5C 5S TC KC JD 6C TS 3C",
    "QD AS 6H JS 2C 3D 9H KC 4H 8S",
    "KD 8S 9S 7C 2S 3S 6D 6S 4H KC",
    "3C 8C 2D 7D 4D 9S 4S QH 4H JD",
    "8C KC 7S TC 2D TS 8H QD AC 5C",
    "3D KH QD 6C 6S AD AS 8H 2H QS",
    "6S 8D 4C 8S 6C QH TC 6D 7D 9D",
    "2S 8D 8C 4C TS 9S 9D 9C AC 3D",
    "3C QS 2S 4H JH 3D 2D TD 8S 9H",
    "5H QS 8S 6D 3C 8C JD AS 7H 7D",
    "6H TD 9D AS JH 6C QC 9S KD JC",
    "AH 8S QS 4D TH AC TS 3C 3D 5C",
    "5S 4D JS 3D 8H 6C TS 3S AD 8C",
    "6D 7C 5D 5H 3S 5C JC 2H 5S 3D",
    "5H 6H 2S KS 3D 5D JD 7H JS 8H",
    "KH 4H AS JS QS QC TC 6D 7C KS",
    "3D QS TS 2H JS 4D AS 9S JC KD",
    "QD 5H 4D 5D KH 7H 3D JS KD 4H",
    "2C 9H 6H 5C 9D 6C JC 2D TH 9S",
    "7D 6D AS QD JH 4D JS 7C QS 5C",
    "3H KH QD AD 8C 8H 3S TH 9D 5S",
    "AH 9S 4D 9D 8S 4H JS 3C TC 8D",
    "2C KS 5H QD 3S TS 9H AH AD 8S",
    "5C 7H 5D KD 9H 4D 3D 2D KS AD",
    "KS KC 9S 6D 2C QH 9D 9H TS TC",
    "9C 6H 5D QH 4D AD 6D QC JS KH",
    "9S 3H 9D JD 5C 4D 9H AS TC QH",
    "2C 6D JC 9C 3C AD 9S KH 9D 7D",
    "KC 9C 7C JC JS KD 3H AS 3C 7D",
    "QD KH QS 2C 3S 8S 8H 9H 9C JC",
    "QH 8D 3C KC 4C 4H 6D AD 9H 9D",
    "3S KS QS 7H KH 7D 5H 5D JD AD",
    "2H 2C 6H TH TC 7D 8D 4H 8C AS",
    "4S 2H AC QC 3S 6D TH 4D 4C KH",
    "4D TC KS AS 7C 3C 6D 2D 9H 6C",
    "8C TD 5D QS 2C 7H 4C 9C 3H 9H",
    "5H JH TS 7S TD 6H AD QD 8H 8S",
    "5S AD 9C 8C 7C 8D 5H 9D 8S 2S",
    "4H KH KS 9S 2S KC 5S AD 4S 7D",
    "QS 9C QD 6H JS 5D AC 8D 2S AS",
    "KH AC JC 3S 9D 9S 3C 9C 5S JS",
    "AD 3C 3D KS 3S 5C 9C 8C TS 4S",
    "JH 8D 5D 6H KD QS QD 3D 6C KC",
    "8S JD 6C 3S 8C TC QC 3C QH JS",
    "KC JC 8H 2S 9H 9C JH 8S 8C 9S",
    "8S 2H QH 4D QC 9D KC AS TH 3C",
    "8S 6H TH 7C 2H 6S 3C 3H AS 7S",
    "QH 5S JS 4H 5H TS 8H AH AC JC",
    "9D 8H 2S 4S TC JC 3C 7H 3H 5C",
    "3D AD 3C 3S 4C QC AS 5D TH 8C",
    "6S 9D 4C JS KH AH TS JD 8H AD",
    "4C 6S 9D 7S AC 4D 3D 3S TC JD",
    "AD 7H 6H 4H JH KC TD TS 7D 6S",
    "8H JH TC 3S 8D 8C 9S 2C 5C 4D",
    "2C 9D KC QH TH QS JC 9C 4H TS",
    "QS 3C QD 8H KH 4H 8D TD 8S AC",
    "7C 3C TH 5S 8H 8C 9C JD TC KD",
    "QC TC JD TS 8C 3H 6H KD 7C TD",
    "JH QS KS 9C 6D 6S AS 9H KH 6H",
    "2H 4D AH 2D JH 6H TD 5D 4H JD",
    "KD 8C 9S JH QD JS 2C QS 5C 7C",
    "4S TC 7H 8D 2S 6H 7S 9C 7C KC",
    "8C 5D 7H 4S TD QC 8S JS 4H KS",
    "AD 8S JH 6D TD KD 7C 6C 2D 7D",
    "JC 6H 6S JS 4H QH 9H AH 4C 3C",
    "6H 5H AS 7C 7S 3D KH KC 5D 5C",
    "JC 3D TD AS 4D 6D 6S QH JD KS",
    "8C 7S 8S QH 2S JD 5C 7H AH QD",
    "8S 3C 6H 6C 2C 8D TD 7D 4C 4D",
    "5D QH KH 7C 2S 7H JS 6D QC QD",
    "AD 6C 6S 7D TH 6H 2H 8H KH 4H",
    "KS JS KD 5D 2D KH 7D 9C 8C 3D",
    "9C 6D QD 3C KS 3S 7S AH JD 2D",
    "AH QH AS JC 8S 8H 4C KC TH 7D",
    "JC 5H TD 7C 5D KD 4C AD 8H JS",
    "KC 2H AC AH 7D JH KH 5D 7S 6D",
    "9S 5S 9C 6H 8S TD JD 9H 6C AC",
    "7D 8S 6D TS KD 7H AC 5S 7C 5D",
    "AH QC JC 4C TC 8C 2H TS 2C 7D",
    "KD KC 6S 3D 7D 2S 8S 3H 5S 5C",
    "8S 5D 8H 4C 6H KC 3H 7C 5S KD",
    "JH 8C 3D 3C 6C KC TD 7H 7C 4C",
    "JC KC 6H TS QS TD KS 8H 8C 9S",
    "6C 5S 9C QH 7D AH KS KC 9S 2C",
    "4D 4S 8H TD 9C 3S 7D 9D AS TH",
    "6S 7D 3C 6H 5D KD 2C 5C 9D 9C",
    "2H KC 3D AD 3H QD QS 8D JC 4S",
    "8C 3H 9C 7C AD 5D JC 9D JS AS",
    "5D 9H 5C 7H 6S 6C QC JC QD 9S",
    "JC QS JH 2C 6S 9C QC 3D 4S TC",
    "4H 5S 8D 3D 4D 2S KC 2H JS 2C",
    "TD 3S TH KD 4D 7H JH JS KS AC",
    "7S 8C 9S 2D 8S 7D 5C AD 9D AS",
    "8C 7H 2S 6C TH 3H 4C 3S 8H AC",
    "KD 5H JC 8H JD 2D 4H TD JH 5C",
    "3D AS QH KS 7H JD 8S 5S 6D 5H",
    "9S 6S TC QS JC 5C 5D 9C TH 8C",
    "5H 3S JH 9H 2S 2C 6S 7S AS KS",
    "8C QD JC QS TC QC 4H AC KH 6C",
    "TC 5H 7D JH 4H 2H 8D JC KS 4D",
    "5S 9C KH KD 9H 5C TS 3D 7D 2D",
    "5H AS TC 4D 8C 2C TS 9D 3H 8D",
    "6H 8D 2D 9H JD 6C 4S 5H 5S 6D",
    "AD 9C JC 7D 6H 9S 6D JS 9H 3C",
    "AD JH TC QS 4C 5D 9S 7C 9C AH",
    "KD 6H 2H TH 8S QD KS 9D 9H AS",
    "4H 8H 8D 5H 6C AH 5S AS AD 8S",
    "QS 5D 4S 2H TD KS 5H AC 3H JC",
    "9C 7D QD KD AC 6D 5H QH 6H 5S",
    "KC AH QH 2H 7D QS 3H KS 7S JD",
    "6C 8S 3H 6D KS QD 5D 5C 8H TC",
    "9H 4D 4S 6S 9D KH QC 4H 6C JD",
    "TD 2D QH 4S 6H JH KD 3C QD 8C",
    "4S 6H 7C QD 9D AS AH 6S AD 3C",
    "2C KC TH 6H 8D AH 5C 6D 8S 5D",
    "TD TS 7C AD JC QD 9H 3C KC 7H",
    "5D 4D 5S 8H 4H 7D 3H JD KD 2D",
    "JH TD 6H QS 4S KD 5C 8S 7D 8H",
    "AC 3D AS 8C TD 7H KH 5D 6C JD",
    "9D KS 7C 6D QH TC JD KD AS KC",
    "JH 8S 5S 7S 7D AS 2D 3D AD 2H",
    "2H 5D AS 3C QD KC 6H 9H 9S 2C",
    "9D 5D TH 4C JH 3H 8D TC 8H 9H",
    "6H KD 2C TD 2H 6C 9D 2D JS 8C",
    "KD 7S 3C 7C AS QH TS AD 8C 2S",
    "QS 8H 6C JS 4C 9S QC AD TD TS",
    "2H 7C TS TC 8C 3C 9H 2D 6D JC",
    "TC 2H 8D JH KS 6D 3H TD TH 8H",
    "9D TD 9H QC 5D 6C 8H 8C KC TS",
    "2H 8C 3D AH 4D TH TC 7D 8H KC",
    "TS 5C 2D 8C 6S KH AH 5H 6H KC",
    "5S 5D AH TC 4C JD 8D 6H 8C 6C",
    "KC QD 3D 8H 2D JC 9H 4H AD 2S",
    "TD 6S 7D JS KD 4H QS 2S 3S 8C",
    "4C 9H JH TS 3S 4H QC 5S 9S 9C",
    "2C KD 9H JS 9S 3H JC TS 5D AC",
    "AS 2H 5D AD 5H JC 7S TD JS 4C",
    "2D 4S 8H 3D 7D 2C AD KD 9C TS",
    "7H QD JH 5H JS AC 3D TH 4C 8H",
    "6D KH KC QD 5C AD 7C 2D 4H AC",
    "3D 9D TC 8S QD 2C JC 4H JD AH",
    "6C TD 5S TC 8S AH 2C 5D AS AC",
    "TH 7S 3D AS 6C 4C 7H 7D 4H AH",
    "5C 2H KS 6H 7S 4H 5H 3D 3C 7H",
    "3C 9S AC 7S QH 2H 3D 6S 3S 3H",
    "2D 3H AS 2C 6H TC JS 6S 9C 6C",
    "QH KD QD 6D AC 6H KH 2C TS 8C",
    "8H 7D 3S 9H 5D 3H 4S QC 9S 5H",
    "2D 9D 7H 6H 3C 8S 5H 4D 3S 4S",
    "KD 9S 4S TC 7S QC 3S 8S 2H 7H",
    "TC 3D 8C 3H 6C 2H 6H KS KD 4D",
    "KC 3D 9S 3H JS 4S 8H 2D 6C 8S",
    "6H QS 6C TC QD 9H 7D 7C 5H 4D",
    "TD 9D 8D 6S 6C TC 5D TS JS 8H",
    "4H KC JD 9H TC 2C 6S 5H 8H AS",
    "JS 9C 5C 6S 9D JD 8H KC 4C 6D",
    "4D 8D 8S 6C 7C 6H 7H 8H 5C KC",
    "TC 3D JC 6D KS 9S 6H 7S 9C 2C",
    "6C 3S KD 5H TS 7D 9H 9S 6H KH",
    "3D QD 4C 6H TS AC 3S 5C 2H KD",
    "4C AS JS 9S 7C TS 7H 9H JC KS",
    "4H 8C JD 3H 6H AD 9S 4S 5S KS",
    "4C 2C 7D 3D AS 9C 2S QS KC 6C",
    "8S 5H 3D 2S AC 9D 6S 3S 4D TD",
    "QD TH 7S TS 3D AC 7H 6C 5D QC",
    "TC QD AD 9C QS 5C 8D KD 3D 3C",
    "9D 8H AS 3S 7C 8S JD 2D 8D KC",
    "4C TH AC QH JS 8D 7D 7S 9C KH",
    "9D 8D 4C JH 2C 2S QD KD TS 4H",
    "4D 6D 5D 2D JH 3S 8S 3H TC KH",
    "AD 4D 2C QS 8C KD JH JD AH 5C",
    "5C 6C 5H 2H JH 4H KS 7C TC 3H",
    "3C 4C QC 5D JH 9C QD KH 8D TC",
    "3H 9C JS 7H QH AS 7C 9H 5H JC",
    "2D 5S QD 4S 3C KC 6S 6C 5C 4C",
    "5D KH 2D TS 8S 9C AS 9S 7C 4C",
    "7C AH 8C 8D 5S KD QH QS JH 2C",
    "8C 9D AH 2H AC QC 5S 8H 7H 2C",
    "QD 9H 5S QS QC 9C 5H JC TH 4H",
    "6C 6S 3H 5H 3S 6H KS 8D AC 7S",
    "AC QH 7H 8C 4S KC 6C 3D 3S TC",
    "9D 3D JS TH AC 5H 3H 8S 3S TC",
    "QD KH JS KS 9S QC 8D AH 3C AC",
    "5H 6C KH 3S 9S JH 2D QD AS 8C",
    "6C 4D 7S 7H 5S JC 6S 9H 4H JH",
    "AH 5S 6H 9S AD 3S TH 2H 9D 8C",
    "4C 8D 9H 7C QC AD 4S 9C KC 5S",
    "9D 6H 4D TC 4C JH 2S 5D 3S AS",
    "2H 6C 7C KH 5C AD QS TH JD 8S",
    "3S 4S 7S AH AS KC JS 2S AD TH",
    "JS KC 2S 7D 8C 5C 9C TS 5H 9D",
    "7S 9S 4D TD JH JS KH 6H 5D 2C",
    "JD JS JC TH 2D 3D QD 8C AC 5H",
    "7S KH 5S 9D 5D TD 4S 6H 3C 2D",
    "4S 5D AC 8D 4D 7C AD AS AH 9C",
    "6S TH TS KS 2C QC AH AS 3C 4S",
    "2H 8C 3S JC 5C 7C 3H 3C KH JH",
    "7S 3H JC 5S 6H 4C 2S 4D KC 7H",
    "4D 7C 4H 9S 8S 6S AD TC 6C JC",
    "KH QS 3S TC 4C 8H 8S AC 3C TS",
    "QD QS TH 3C TS 7H 7D AH TD JC",
    "TD JD QC 4D 9S 7S TS AD 7D AC",
    "AH 7H 4S 6D 7C 2H 9D KS JC TD",
    "7C AH JD 4H 6D QS TS 2H 2C 5C",
    "TC KC 8C 9S 4C JS 3C JC 6S AH",
    "AS 7D QC 3D 5S JC JD 9D TD KH",
    "TH 3C 2S 6H AH AC 5H 5C 7S 8H",
    "QC 2D AC QD 2S 3S JD QS 6S 8H",
    "KC 4H 3C 9D JS 6H 3S 8S AS 8C",
    "7H KC 7D JD 2H JC QH 5S 3H QS",
    "9H TD 3S 8H 7S AC 5C 6C AH 7C",
    "8D 9H AH JD TD QS 7D 3S 9C 8S",
    "AH QH 3C JD KC 4S 5S 5D TD KS",
    "9H 7H 6S JH TH 4C 7C AD 5C 2D",
    "7C KD 5S TC 9D 6S 6C 5D 2S TH",
    "KC 9H 8D 5H 7H 4H QC 3D 7C AS",
    "6S 8S QC TD 4S 5C TH QS QD 2S",
    "8S 5H TH QC 9H 6S KC 7D 7C 5C",
    "7H KD AH 4D KH 5C 4S 2D KC QH",
    "6S 2C TD JC AS 4D 6C 8C 4H 5S",
    "JC TC JD 5S 6S 8D AS 9D AD 3S",
    "6D 6H 5D 5S TC 3D 7D QS 9D QD",
    "4S 6C 8S 3S 7S AD KS 2D 7D 7C",
    "KC QH JC AC QD 5D 8D QS 7H 7D",
    "JS AH 8S 5H 3D TD 3H 4S 6C JH",
    "4S QS 7D AS 9H JS KS 6D TC 5C",
    "2D 5C 6H TC 4D QH 3D 9H 8S 6C",
    "6D 7H TC TH 5S JD 5C 9C KS KD",
    "8D TD QH 6S 4S 6C 8S KC 5C TC",
    "5S 3D KS AC 4S 7D QD 4C TH 2S",
    "TS 8H 9S 6S 7S QH 3C AH 7H 8C",
    "4C 8C TS JS QC 3D 7D 5D 7S JH",
    "8S 7S 9D QC AC 7C 6D 2H JH KC",
    "JS KD 3C 6S 4S 7C AH QC KS 5H",
    "KS 6S 4H JD QS TC 8H KC 6H AS",
    "KH 7C TC 6S TD JC 5C 7D AH 3S",
    "3H 4C 4H TC TH 6S 7H 6D 9C QH",
    "7D 5H 4S 8C JS 4D 3D 8S QH KC",
    "3H 6S AD 7H 3S QC 8S 4S 7S JS",
    "3S JD KH TH 6H QS 9C 6C 2D QD",
    "4S QH 4D 5H KC 7D 6D 8D TH 5S",
    "TD AD 6S 7H KD KH 9H 5S KC JC",
    "3H QC AS TS 4S QD KS 9C 7S KC",
    "TS 6S QC 6C TH TC 9D 5C 5D KD",
    "JS 3S 4H KD 4C QD 6D 9S JC 9D",
    "8S JS 6D 4H JH 6H 6S 6C KS KH",
    "AC 7D 5D TC 9S KH 6S QD 6H AS",
    "AS 7H 6D QH 8D TH 2S KH 5C 5H",
    "4C 7C 3D QC TC 4S KH 8C 2D JS",
    "6H 5D 7S 5H 9C 9H JH 8S TH 7H",
    "AS JS 2S QD KH 8H 4S AC 8D 8S",
    "3H 4C TD KD 8C JC 5C QS 2D JD",
    "TS 7D 5D 6C 2C QS 2H 3C AH KS",
    "4S 7C 9C 7D JH 6C 5C 8H 9D QD",
    "2S TD 7S 6D 9C 9S QS KH QH 5C",
    "JC 6S 9C QH JH 8D 7S JS KH 2H",
    "8D 5H TH KC 4D 4S 3S 6S 3D QS",
    "2D JD 4C TD 7C 6D TH 7S JC AH",
    "QS 7S 4C TH 9D TS AD 4D 3H 6H",
    "2D 3H 7D JD 3D AS 2S 9C QC 8S",
    "4H 9H 9C 2C 7S JH KD 5C 5D 6H",
    "TC 9H 8H JC 3C 9S 8D KS AD KC",
    "TS 5H JD QS QH QC 8D 5D KH AH",
    "5D AS 8S 6S 4C AH QC QD TH 7H",
    "3H 4H 7D 6S 4S 9H AS 8H JS 9D",
    "JD 8C 2C 9D 7D 5H 5S 9S JC KD",
    "KD 9C 4S QD AH 7C AD 9D AC TD",
    "6S 4H 4S 9C 8D KS TC 9D JH 7C",
    "5S JC 5H 4S QH AC 2C JS 2S 9S",
    "8C 5H AS QD AD 5C 7D 8S QC TD",
    "JC 4C 8D 5C KH QS 4D 6H 2H 2C",
    "TH 4S 2D KC 3H QD AC 7H AD 9D",
    "KH QD AS 8H TH KC 8D 7S QH 8C",
    "JC 6C 7D 8C KH AD QS 2H 6S 2D",
    "JC KH 2D 7D JS QC 5H 4C 5D AD",
    "TS 3S AD 4S TD 2D TH 6S 9H JH",
    "9H 2D QS 2C 4S 3D KH AS AC 9D",
    "KH 6S 8H 4S KD 7D 9D TS QD QC",
    "JH 5H AH KS AS AD JC QC 5S KH",
    "5D 7D 6D KS KD 3D 7C 4D JD 3S",
    "AC JS 8D 5H 9C 3H 4H 4D TS 2C",
    "6H KS KH 9D 7C 2S 6S 8S 2H 3D",
    "6H AC JS 7S 3S TD 8H 3H 4H TH",
    "9H TC QC KC 5C KS 6H 4H AC 8S",
    "TC 7D QH 4S JC TS 6D 6C AC KH",
    "QH 7D 7C JH QS QD TH 3H 5D KS",
    "3D 5S 8D JS 4C 2C KS 7H 9C 4H",
    "5H 8S 4H TD 2C 3S QD QC 3H KC",
    "QC JS KD 9C AD 5S 9D 7D 7H TS",
    "8C JC KH 7C 7S 6C TS 2C QD TH",
    "5S 9D TH 3C 7S QH 8S 9C 2H 5H",
    "5D 9H 6H 2S JS KH 3H 7C 2H 5S",
    "JD 5D 5S 2C TC 2S 6S 6C 3C 8S",
    "4D KH 8H 4H 2D KS 3H 5C 2S 9H",
    "3S 2D TD 7H 8S 6H JD KC 9C 8D",
    "6S QD JH 7C 9H 5H 8S 8H TH TD",
    "QS 7S TD 7D TS JC KD 7C 3C 2C",
    "3C JD 8S 4H 2D 2S TD AS 4D AC",
    "AH KS 6C 4C 4S 7D 8C 9H 6H AS",
    "5S 3C 9S 2C QS KD 4D 4S AC 5D",
    "2D TS 2C JS KH QH 5D 8C AS KC",
    "KD 3H 6C TH 8S 7S KH 6H 9S AC",
    "6H 7S 6C QS AH 2S 2H 4H 5D 5H",
    "5H JC QD 2C 2S JD AS QC 6S 7D",
    "6C TC AS KD 8H 9D 2C 7D JH 9S",
    "2H 4C 6C AH 8S TD 3H TH 7C TS",
    "KD 4S TS 6C QH 8D 9D 9C AH 7D",
    "6D JS 5C QD QC 9C 5D 8C 2H KD",
    "3C QH JH AD 6S AH KC 8S 6D 6H",
    "3D 7C 4C 7S 5S 3S 6S 5H JC 3C",
    "QH 7C 5H 3C 3S 8C TS 4C KD 9C",
    "QD 3S 7S 5H 7H QH JC 7C 8C KD",
    "3C KD KH 2S 4C TS AC 6S 2C 7C",
    "2C KH 3C 4C 6H 4D 5H 5S 7S QD",
    "4D 7C 8S QD TS 9D KS 6H KD 3C",
    "QS 4D TS 7S 4C 3H QD 8D 9S TC",
    "TS QH AC 6S 3C 9H 9D QS 8S 6H",
    "3S 7S 5D 4S JS 2D 6C QH 6S TH",
    "4C 4H AS JS 5D 3D TS 9C AC 8S",
    "6S 9C 7C 3S 5C QS AD AS 6H 3C",
    "9S 8C 7H 3H 6S 7C AS 9H JD KH",
    "3D 3H 7S 4D 6C 7C AC 2H 9C TH",
    "4H 5S 3H AC TC TH 9C 9H 9S 8D",
    "8D 9H 5H 4D 6C 2H QD 6S 5D 3S",
    "4C 5C JD QS 4D 3H TH AC QH 8C",
    "QC 5S 3C 7H AD 4C KS 4H JD 6D",
    "QS AH 3H KS 9H 2S JS JH 5H 2H",
    "2H 5S TH 6S TS 3S KS 3C 5H JS",
    "2D 9S 7H 3D KC JH 6D 7D JS TD",
    "AC JS 8H 2C 8C JH JC 2D TH 7S",
    "5D 9S 8H 2H 3D TC AH JC KD 9C",
    "9D QD JC 2H 6D KH TS 9S QH TH",
    "2C 8D 4S JD 5H 3H TH TC 9C KC",
    "AS 3D 9H 7D 4D TH KH 2H 7S 3H",
    "4H 7S KS 2S JS TS 8S 2H QD 8D",
    "5S 6H JH KS 8H 2S QC AC 6S 3S",
    "JC AS AD QS 8H 6C KH 4C 4D QD",
    "2S 3D TS TD 9S KS 6S QS 5C 8D",
    "3C 6D 4S QC KC JH QD TH KH AD",
    "9H AH 4D KS 2S 8D JH JC 7C QS",
    "2D 6C TH 3C 8H QD QH 2S 3S KS",
    "6H 5D 9S 4C TS TD JS QD 9D JD",
    "5H 8H KH 8S KS 7C TD AD 4S KD",
    "2C 7C JC 5S AS 6C 7D 8S 5H 9C",
    "6S QD 9S TS KH QS 5S QH 3C KC",
    "7D 3H 3C KD 5C AS JH 7H 6H JD",
    "9D 5C 9H KC 8H KS 4S AD 4D 2S",
    "3S JD QD 8D 2S 7C 5S 6S 5H TS",
    "6D 9S KC TD 3S 6H QD JD 5C 8D",
    "5H 9D TS KD 8D 6H TD QC 4C 7D",
    "6D 4S JD 9D AH 9S AS TD 9H QD",
    "2D 5S 2H 9C 6H 9S TD QC 7D TC",
    "3S 2H KS TS 2C 9C 8S JS 9D 7D",
    "3C KC 6D 5D 6C 6H 8S AS 7S QS",
    "JH 9S 2H 8D 4C 8H 9H AD TH KH",
    "QC AS 2S JS 5C 6H KD 3H 7H 2C",
    "QD 8H 2S 8D 3S 6D AH 2C TC 5C",
    "JD JS TS 8S 3H 5D TD KC JC 6H",
    "6S QS TC 3H 5D AH JC 7C 7D 4H",
    "7C 5D 8H 9C 2H 9H JH KH 5S 2C",
    "9C 7H 6S TH 3S QC QD 4C AC JD",
    "2H 5D 9S 7D KC 3S QS 2D AS KH",
    "2S 4S 2H 7D 5C TD TH QH 9S 4D",
    "6D 3S TS 6H 4H KS 9D 8H 5S 2D",
    "9H KS 4H 3S 5C 5D KH 6H 6S JS",
    "KC AS 8C 4C JC KH QC TH QD AH",
    "6S KH 9S 2C 5H TC 3C 7H JC 4D",
    "JD 4S 6S 5S 8D 7H 7S 4D 4C 2H",
    "7H 9H 5D KH 9C 7C TS TC 7S 5H",
    "4C 8D QC TS 4S 9H 3D AD JS 7C",
    "8C QS 5C 5D 3H JS AH KC 4S 9D",
    "TS JD 8S QS TH JH KH 2D QD JS",
    "JD QC 5D 6S 9H 3S 2C 8H 9S TS",
    "2S 4C AD 7H JC 5C 2D 6D 4H 3D",
    "7S JS 2C 4H 8C AD QD 9C 3S TD",
    "JD TS 4C 6H 9H 7D QD 6D 3C AS",
    "AS 7C 4C 6S 5D 5S 5C JS QC 4S",
    "KD 6S 9S 7C 3C 5S 7D JH QD JS",
    "4S 7S JH 2C 8S 5D 7H 3D QH AD",
    "TD 6H 2H 8D 4H 2D 7C AD KH 5D",
    "TS 3S 5H 2C QD AH 2S 5C KH TD",
    "KC 4D 8C 5D AS 6C 2H 2S 9H 7C",
    "KD JS QC TS QS KH JH 2C 5D AD",
    "3S 5H KC 6C 9H 3H 2H AD 7D 7S",
    "7S JS JH KD 8S 7D 2S 9H 7C 2H",
    "9H 2D 8D QC 6S AD AS 8H 5H 6C",
    "2S 7H 6C 6D 7D 8C 5D 9D JC 3C",
    "7C 9C 7H JD 2H KD 3S KH AD 4S",
    "QH AS 9H 4D JD KS KD TS KH 5H",
    "4C 8H 5S 3S 3D 7D TD AD 7S KC",
    "JS 8S 5S JC 8H TH 9C 4D 5D KC",
    "7C 5S 9C QD 2C QH JS 5H 8D KH",
    "TD 2S KS 3D AD KC 7S TC 3C 5D",
    "4C 2S AD QS 6C 9S QD TH QH 5C",
    "8C AD QS 2D 2S KC JD KS 6C JC",
    "8D 4D JS 2H 5D QD 7S 7D QH TS",
    "6S 7H 3S 8C 8S 9D QS 8H 6C 9S",
    "4S TC 2S 5C QD 4D QS 6D TH 6S",
    "3S 5C 9D 6H 8D 4C 7D TC 7C TD",
    "AH 6S AS 7H 5S KD 3H 5H AC 4C",
    "8D 8S AH KS QS 2C AD 6H 7D 5D",
    "6H 9H 9S 2H QS 8S 9C 5D 2D KD",
    "TS QC 5S JH 7D 7S TH 9S 9H AC",
    "7H 3H 6S KC 4D 6D 5C 4S QD TS",
    "TD 2S 7C QD 3H JH 9D 4H 7S 7H",
    "KS 3D 4H 5H TC 2S AS 2D 6D 7D",
    "8H 3C 7H TD 3H AD KC TH 9C KH",
    "TC 4C 2C 9S 9D 9C 5C 2H JD 3C",
    "3H AC TS 5D AD 8D 6H QC 6S 8C",
    "2S TS 3S JD 7H 8S QH 4C 5S 8D",
    "AC 4S 6C 3C KH 3D 7C 2D 8S 2H",
    "4H 6C 8S TH 2H 4S 8H 9S 3H 7S",
    "7C 4C 9C 2C 5C AS 5D KD 4D QH",
    "9H 4H TS AS 7D 8D 5D 9S 8C 2H",
    "QC KD AC AD 2H 7S AS 3S 2D 9S",
    "2H QC 8H TC 6D QD QS 5D KH 3C",
    "TH JD QS 4C 2S 5S AD 7H 3S AS",
    "7H JS 3D 6C 3S 6D AS 9S AC QS",
    "9C TS AS 8C TC 8S 6H 9D 8D 6C",
    "4D JD 9C KC 7C 6D KS 3S 8C AS",
    "3H 6S TC 8D TS 3S KC 9S 7C AS",
    "8C QC 4H 4S 8S 6C 3S TC AH AC",
    "4D 7D 5C AS 2H 6S TS QC AD TC",
    "QD QC 8S 4S TH 3D AH TS JH 4H",
    "5C 2D 9S 2C 3H 3C 9D QD QH 7D",
    "KC 9H 6C KD 7S 3C 4D AS TC 2D",
    "3D JS 4D 9D KS 7D TH QC 3H 3C",
    "8D 5S 2H 9D 3H 8C 4C 4H 3C TH",
    "JC TH 4S 6S JD 2D 4D 6C 3D 4C",
    "TS 3S 2D 4H AC 2C 6S 2H JH 6H",
    "TD 8S AD TC AH AC JH 9S 6S 7S",
    "6C KC 4S JD 8D 9H 5S 7H QH AH",
    "KD 8D TS JH 5C 5H 3H AD AS JS",
    "2D 4H 3D 6C 8C 7S AD 5D 5C 8S",
    "TD 5D 7S 9C 4S 5H 6C 8C 4C 8S",
    "JS QH 9C AS 5C QS JC 3D QC 7C",
    "JC 9C KH JH QS QC 2C TS 3D AD",
    "5D JH AC 5C 9S TS 4C JD 8C KS",
    "KC AS 2D KH 9H 2C 5S 4D 3D 6H",
    "TH AH 2D 8S JC 3D 8C QH 7S 3S",
    "8H QD 4H JC AS KH KS 3C 9S 6D",
    "9S QH 7D 9C 4S AC 7H KH 4D KD",
    "AH AD TH 6D 9C 9S KD KS QH 4H",
    "QD 6H 9C 7C QS 6D 6S 9D 5S JH",
    "AH 8D 5H QD 2H JC KS 4H KH 5S",
    "5C 2S JS 8D 9C 8C 3D AS KC AH",
    "JD 9S 2H QS 8H 5S 8C TH 5C 4C",
    "QC QS 8C 2S 2C 3S 9C 4C KS KH",
    "2D 5D 8S AH AD TD 2C JS KS 8C",
    "TC 5S 5H 8H QC 9H 6H JD 4H 9S",
    "3C JH 4H 9H AH 4S 2H 4C 8D AC",
    "8S TH 4D 7D 6D QD QS 7S TC 7C",
    "KH 6D 2D JD 5H JS QD JH 4H 4S",
    "9C 7S JH 4S 3S TS QC 8C TC 4H",
    "QH 9D 4D JH QS 3S 2C 7C 6C 2D",
    "4H 9S JD 5C 5H AH 9D TS 2D 4C",
    "KS JH TS 5D 2D AH JS 7H AS 8D",
    "JS AH 8C AD KS 5S 8H 2C 6C TH",
    "2H 5D AD AC KS 3D 8H TS 6H QC",
    "6D 4H TS 9C 5H JS JH 6S JD 4C",
    "JH QH 4H 2C 6D 3C 5D 4C QS KC",
    "6H 4H 6C 7H 6S 2S 8S KH QC 8C",
    "3H 3D 5D KS 4H TD AD 3S 4D TS",
    "5S 7C 8S 7D 2C KS 7S 6C 8C JS",
    "5D 2H 3S 7C 5C QD 5H 6D 9C 9H",
    "JS 2S KD 9S 8D TD TS AC 8C 9D",
    "5H QD 2S AC 8C 9H KS 7C 4S 3C",
    "KH AS 3H 8S 9C JS QS 4S AD 4D",
    "AS 2S TD AD 4D 9H JC 4C 5H QS",
    "5D 7C 4H TC 2D 6C JS 4S KC 3S",
    "4C 2C 5D AC 9H 3D JD 8S QS QH",
    "2C 8S 6H 3C QH 6D TC KD AC AH",
    "QC 6C 3S QS 4S AC 8D 5C AD KH",
    "5S 4C AC KH AS QC 2C 5C 8D 9C",
    "8H JD 3C KH 8D 5C 9C QD QH 9D",
    "7H TS 2C 8C 4S TD JC 9C 5H QH",
    "JS 4S 2C 7C TH 6C AS KS 7S JD",
    "JH 7C 9H 7H TC 5H 3D 6D 5D 4D",
    "2C QD JH 2H 9D 5S 3D TD AD KS",
    "JD QH 3S 4D TH 7D 6S QS KS 4H",
    "TC KS 5S 8D 8H AD 2S 2D 4C JH",
    "5S JH TC 3S 2D QS 9D 4C KD 9S",
    "AC KH 3H AS 9D KC 9H QD 6C 6S",
    "9H 7S 3D 5C 7D KC TD 8H 4H 6S",
    "3C 7H 8H TC QD 4D 7S 6S QH 6C",
    "6D AD 4C QD 6C 5D 7D 9D KS TS",
    "JH 2H JD 9S 7S TS KH 8D 5D 8H",
    "2D 9S 4C 7D 9D 5H QD 6D AC 6S",
    "7S 6D JC QD JH 4C 6S QS 2H 7D",
    "8C TD JH KD 2H 5C QS 2C JS 7S",
    "TC 5H 4H JH QD 3S 5S 5D 8S KH",
    "KS KH 7C 2C 5D JH 6S 9C 6D JC",
    "5H AH JD 9C JS KC 2H 6H 4D 5S",
    "AS 3C TH QC 6H 9C 8S 8C TD 7C",
    "KC 2C QD 9C KH 4D 7S 3C TS 9H",
    "9C QC 2S TS 8C TD 9S QD 3S 3C",
    "4D 9D TH JH AH 6S 2S JD QH JS",
    "QD 9H 6C KD 7D 7H 5D 6S 8H AH",
    "8H 3C 4S 2H 5H QS QH 7S 4H AC",
    "QS 3C 7S 9S 4H 3S AH KS 9D 7C",
    "AD 5S 6S 2H 2D 5H TC 4S 3C 8C",
    "QH TS 6S 4D JS KS JH AS 8S 6D",
    "2C 8S 2S TD 5H AS TC TS 6C KC",
    "KC TS 8H 2H 3H 7C 4C 5S TH TD",
    "KD AD KH 7H 7S 5D 5H 5S 2D 9C",
    "AD 9S 3D 7S 8C QC 7C 9C KD KS",
    "3C QC 9S 8C 4D 5C AS QD 6C 2C",
    "2H KC 8S JD 7S AC 8D 5C 2S 4D",
    "9D QH 3D 2S TC 3S KS 3C 9H TD",
    "KD 6S AC 2C 7H 5H 3S 6C 6H 8C",
    "QH TC 8S 6S KH TH 4H 5D TS 4D",
    "8C JS 4H 6H 2C 2H 7D AC QD 3D",
    "QS KC 6S 2D 5S 4H TD 3H JH 4C",
    "7S 5H 7H 8H KH 6H QS TH KD 7D",
    "5H AD KD 7C KH 5S TD 6D 3C 6C",
    "8C 9C 5H JD 7C KC KH 7H 2H 3S",
    "7S 4H AD 4D 8S QS TH 3D 7H 5S",
    "8D TC KS KD 9S 6D AD JD 5C 2S",
    "7H 8H 6C QD 2H 6H 9D TC 9S 7C",
    "8D 6D 4C 7C 6C 3C TH KH JS JH",
    "5S 3S 8S JS 9H AS AD 8H 7S KD",
    "JH 7C 2C KC 5H AS AD 9C 9S JS",
    "AD AC 2C 6S QD 7C 3H TH KS KD",
    "9D JD 4H 8H 4C KH 7S TS 8C KC",
    "3S 5S 2H 7S 6H 7D KS 5C 6D AD",
    "5S 8C 9H QS 7H 7S 2H 6C 7D TD",
    "QS 5S TD AC 9D KC 3D TC 2D 4D",
    "TD 2H 7D JD QD 4C 7H 5D KC 3D",
    "4C 3H 8S KD QH 5S QC 9H TC 5H",
    "9C QD TH 5H TS 5C 9H AH QH 2C",
    "4D 6S 3C AC 6C 3D 2C 2H TD TH",
    "AC 9C 5D QC 4D AD 8D 6D 8C KC",
    "AD 3C 4H AC 8D 8H 7S 9S TD JC",
    "4H 9H QH JS 2D TH TD TC KD KS",
    "5S 6S 9S 8D TH AS KH 5H 5C 8S",
    "JD 2S 9S 6S 5S 8S 5D 7S 7H 9D",
    "5D 8C 4C 9D AD TS 2C 7D KD TC",
    "8S QS 4D KC 5C 8D 4S KH JD KD",
    "AS 5C AD QH 7D 2H 9S 7H 7C TC",
    "2S 8S JD KH 7S 6C 6D AD 5D QC",
    "9H 6H 3S 8C 8H AH TC 4H JS TD",
    "2C TS 4D 7H 2D QC 9C 5D TH 7C",
    "6C 8H QC 5D TS JH 5C 5H 9H 4S",
    "2D QC 7H AS JS 8S 2H 4C 4H 8D",
    "JS 6S AC KD 3D 3C 4S 7H TH KC",
    "QH KH 6S QS 5S 4H 3C QD 3S 3H",
    "7H AS KH 8C 4H 9C 5S 3D 6S TS",
    "9C 7C 3H 5S QD 2C 3D AD AC 5H",
    "JH TD 2D 4C TS 3H KH AD 3S 7S",
    "AS 4C 5H 4D 6S KD JC 3C 6H 2D",
    "3H 6S 8C 2D TH 4S AH QH AD 5H",
    "7C 2S 9H 7H KC 5C 6D 5S 3H JC",
    "3C TC 9C 4H QD TD JH 6D 9H 5S",
    "7C 6S 5C 5D 6C 4S 7H 9H 6H AH",
    "AD 2H 7D KC 2C 4C 2S 9S 7H 3S",
    "TH 4C 8S 6S 3S AD KS AS JH TD",
    "5C TD 4S 4D AD 6S 5D TC 9C 7D",
    "8H 3S 4D 4S 5S 6H 5C AC 3H 3D",
    "9H 3C AC 4S QS 8S 9D QH 5H 4D",
    "JC 6C 5H TS AC 9C JD 8C 7C QD",
    "8S 8H 9C JD 2D QC QH 6H 3C 8D",
    "KS JS 2H 6H 5H QH QS 3H 7C 6D",
    "TC 3H 4S 7H QC 2H 3S 8C JS KH",
    "AH 8H 5S 4C 9H JD 3H 7S JC AC",
    "3C 2D 4C 5S 6C 4S QS 3S JD 3D",
    "5H 2D TC AH KS 6D 7H AD 8C 6H",
    "6C 7S 3C JD 7C 8H KS KH AH 6D",
    "AH 7D 3H 8H 8S 7H QS 5H 9D 2D",
    "JD AC 4H 7S 8S 9S KS AS 9D QH",
    "7S 2C 8S 5S JH QS JC AH KD 4C",
    "AH 2S 9H 4H 8D TS TD 6H QH JD",
    "4H JC 3H QS 6D 7S 9C 8S 9D 8D",
    "5H TD 4S 9S 4C 8C 8D 7H 3H 3D",
    "QS KH 3S 2C 2S 3C 7S TD 4S QD",
    "7C TD 4D 5S KH AC AS 7H 4C 6C",
    "2S 5H 6D JD 9H QS 8S 2C 2H TD",
    "2S TS 6H 9H 7S 4H JC 4C 5D 5S",
    "2C 5H 7D 4H 3S QH JC JS 6D 8H",
    "4C QH 7C QD 3S AD TH 8S 5S TS",
    "9H TC 2S TD JC 7D 3S 3D TH QH",
    "7D 4C 8S 5C JH 8H 6S 3S KC 3H",
    "JC 3H KH TC QH TH 6H 2C AC 5H",
    "QS 2H 9D 2C AS 6S 6C 2S 8C 8S",
    "9H 7D QC TH 4H KD QS AC 7S 3C",
    "4D JH 6S 5S 8H KS 9S QC 3S AS",
    "JD 2D 6S 7S TC 9H KC 3H 7D KD",
    "2H KH 7C 4D 4S 3H JS QD 7D KC",
    "4C JC AS 9D 3C JS 6C 8H QD 4D",
    "AH JS 3S 6C 4C 3D JH 6D 9C 9H",
    "9H 2D 8C 7H 5S KS 6H 9C 2S TC",
    "6C 8C AD 7H 6H 3D KH AS 5D TH",
    "KS 8C 3S TS 8S 4D 5S 9S 6C 4H",
    "9H 4S 4H 5C 7D KC 2D 2H 9D JH",
    "5C JS TC 9D 9H 5H 7S KH JC 6S",
    "7C 9H 8H 4D JC KH JD 2H TD TC",
    "8H 6C 2H 2C KH 6H 9D QS QH 5H",
    "AC 7D 2S 3D QD JC 2D 8D JD JH",
    "2H JC 2D 7H 2C 3C 8D KD TD 4H",
    "3S 4H 6D 8D TS 3H TD 3D 6H TH",
    "JH JC 3S AC QH 9H 7H 8S QC 2C",
    "7H TD QS 4S 8S 9C 2S 5D 4D 2H",
    "3D TS 3H 2S QC 8H 6H KC JC KS",
    "5D JD 7D TC 8C 6C 9S 3D 8D AC",
    "8H 6H JH 6C 5D 8D 8S 4H AD 2C",
    "9D 4H 2D 2C 3S TS AS TC 3C 5D",
    "4D TH 5H KS QS 6C 4S 2H 3D AD",
    "5C KC 6H 2C 5S 3C 4D 2D 9H 9S",
    "JD 4C 3H TH QH 9H 5S AH 8S AC",
    "7D 9S 6S 2H TD 9C 4H 8H QS 4C",
    "3C 6H 5D 4H 8C 9C KC 6S QD QS",
    "3S 9H KD TC 2D JS 8C 6S 4H 4S",
    "2S 4C 8S QS 6H KH 3H TH 8C 5D",
    "2C KH 5S 3S 7S 7H 6C 9D QD 8D",
    "8H KS AC 2D KH TS 6C JS KC 7H",
    "9C KS 5C TD QC AH 6C 5H 9S 7C",
    "5D 4D 3H 4H 6S 7C 7S AH QD TD",
    "2H 7D QC 6S TC TS AH 7S 9D 3H",
    "TH 5H QD 9S KS 7S 7C 6H 8C TD",
    "TH 2D 4D QC 5C 7D JD AH 9C 4H",
    "4H 3H AH 8D 6H QC QH 9H 2H 2C",
    "2D AD 4C TS 6H 7S TH 4H QS TD",
    "3C KD 2H 3H QS JD TC QC 5D 8H",
    "KS JC QD TH 9S KD 8D 8C 2D 9C",
    "3C QD KD 6D 4D 8D AH AD QC 8S",
    "8H 3S 9D 2S 3H KS 6H 4C 7C KC",
    "TH 9S 5C 3D 7D 6H AC 7S 4D 2C",
    "5C 3D JD 4D 2D 6D 5H 9H 4C KH",
    "AS 7H TD 6C 2H 3D QD KS 4C 4S",
    "JC 3C AC 7C JD JS 8H 9S QC 5D",
    "JD 6S 5S 2H AS 8C 7D 5H JH 3D",
    "8D TC 5S 9S 8S 3H JC 5H 7S AS",
    "5C TD 3D 7D 4H 8D 7H 4D 5D JS",
    "QS 9C KS TD 2S 8S 5C 2H 4H AS",
    "TH 7S 4H 7D 3H JD KD 5D 2S KC",
    "JD 7H 4S 8H 4C JS 6H QH 5S 4H",
    "2C QS 8C 5S 3H QC 2S 6C QD AD",
    "8C 3D JD TC 4H 2H AD 5S AC 2S",
    "5D 2C JS 2D AD 9D 3D 4C 4S JH",
    "8D 5H 5D 6H 7S 4D KS 9D TD JD",
    "3D 6D 9C 2S AS 7D 5S 5C 8H JD",
    "7C 8S 3S 6S 5H JD TC AD 7H 7S",
    "2S 9D TS 4D AC 8D 6C QD JD 3H",
    "9S KH 2C 3C AC 3D 5H 6H 8D 5D",
    "KS 3D 2D 6S AS 4C 2S 7C 7H KH",
    "AC 2H 3S JC 5C QH 4D 2D 5H 7S",
    "TS AS JD 8C 6H JC 8S 5S 2C 5D",
    "7S QH 7H 6C QC 8H 2D 7C JD 2S",
    "2C QD 2S 2H JC 9C 5D 2D JD JH",
    "7C 5C 9C 8S 7D 6D 8D 6C 9S JH",
    "2C AD 6S 5H 3S KS 7S 9D KH 4C",
    "7H 6C 2C 5C TH 9D 8D 3S QC AH",
    "5S KC 6H TC 5H 8S TH 6D 3C AH",
    "9C KD 4H AD TD 9S 4S 7D 6H 5D",
    "7H 5C 5H 6D AS 4C KD KH 4H 9D",
    "3C 2S 5C 6C JD QS 2H 9D 7D 3H",
    "AC 2S 6S 7S JS QD 5C QS 6H AD",
    "5H TH QC 7H TC 3S 7C 6D KC 3D",
    "4H 3D QC 9S 8H 2C 3S JC KS 5C",
    "4S 6S 2C 6H 8S 3S 3D 9H 3H JS",
    "4S 8C 4D 2D 8H 9H 7D 9D AH TS",
    "9S 2C 9H 4C 8D AS 7D 3D 6D 5S",
    "6S 4C 7H 8C 3H 5H JC AH 9D 9C",
    "2S 7C 5S JD 8C 3S 3D 4D 7D 6S",
    "3C KC 4S 5D 7D 3D JD 7H 3H 4H",
    "9C 9H 4H 4D TH 6D QD 8S 9S 7S",
    "2H AC 8S 4S AD 8C 2C AH 7D TC",
    "TS 9H 3C AD KS TC 3D 8C 8H JD",
    "QC 8D 2C 3C 7D 7C JD 9H 9C 6C",
    "AH 6S JS JH 5D AS QC 2C JD TD",
    "9H KD 2H 5D 2D 3S 7D TC AH TS",
    "TD 8H AS 5D AH QC AC 6S TC 5H",
    "KS 4S 7H 4D 8D 9C TC 2H 6H 3H",
    "3H KD 4S QD QH 3D 8H 8C TD 7S",
    "8S JD TC AH JS QS 2D KH KS 4D",
    "3C AD JC KD JS KH 4S TH 9H 2C",
    "QC 5S JS 9S KS AS 7C QD 2S JD",
    "KC 5S QS 3S 2D AC 5D 9H 8H KS",
    "6H 9C TC AD 2C 6D 5S JD 6C 7C",
    "QS KH TD QD 2C 3H 8S 2S QC AH",
    "9D 9H JH TC QH 3C 2S JS 5C 7H",
    "6C 3S 3D 2S 4S QD 2D TH 5D 2C",
    "2D 6H 6D 2S JC QH AS 7H 4H KH",
    "5H 6S KS AD TC TS 7C AC 4S 4H",
    "AD 3C 4H QS 8C 9D KS 2H 2D 4D",
    "4S 9D 6C 6D 9C AC 8D 3H 7H KD",
    "JC AH 6C TS JD 6D AD 3S 5D QD",
    "JC JH JD 3S 7S 8S JS QC 3H 4S",
    "JD TH 5C 2C AD JS 7H 9S 2H 7S",
    "8D 3S JH 4D QC AS JD 2C KC 6H",
    "2C AC 5H KD 5S 7H QD JH AH 2D",
    "JC QH 8D 8S TC 5H 5C AH 8C 6C",
    "3H JS 8S QD JH 3C 4H 6D 5C 3S",
    "6D 4S 4C AH 5H 5S 3H JD 7C 8D",
    "8H AH 2H 3H JS 3C 7D QC 4H KD",
    "6S 2H KD 5H 8H 2D 3C 8S 7S QD",
    "2S 7S KC QC AH TC QS 6D 4C 8D",
    "5S 9H 2C 3S QD 7S 6C 2H 7C 9D",
    "3C 6C 5C 5S JD JC KS 3S 5D TS",
    "7C KS 6S 5S 2S 2D TC 2H 5H QS",
    "AS 7H 6S TS 5H 9S 9D 3C KD 2H",
    "4S JS QS 3S 4H 7C 2S AC 6S 9D",
    "8C JH 2H 5H 7C 5D QH QS KH QC",
    "3S TD 3H 7C KC 8D 5H 8S KH 8C",
    "4H KH JD TS 3C 7H AS QC JS 5S",
    "AH 9D 2C 8D 4D 2D 6H 6C KC 6S",
    "2S 6H 9D 3S 7H 4D KH 8H KD 3D",
    "9C TC AC JH KH 4D JD 5H TD 3S",
    "7S 4H 9D AS 4C 7D QS 9S 2S KH",
    "3S 8D 8S KS 8C JC 5C KH 2H 5D",
    "8S QH 2C 4D KC JS QC 9D AC 6H",
    "8S 8C 7C JS JD 6S 4C 9C AC 4S",
    "QH 5D 2C 7D JC 8S 2D JS JH 4C",
    "JS 4C 7S TS JH KC KH 5H QD 4S",
    "QD 8C 8D 2D 6S TD 9D AC QH 5S",
    "QH QC JS 3D 3C 5C 4H KH 8S 7H",
    "7C 2C 5S JC 8S 3H QC 5D 2H KC",
    "5S 8D KD 6H 4H QD QH 6D AH 3D",
    "7S KS 6C 2S 4D AC QS 5H TS JD",
    "7C 2D TC 5D QS AC JS QC 6C KC",
    "2C KS 4D 3H TS 8S AD 4H 7S 9S",
    "QD 9H QH 5H 4H 4D KH 3S JC AD",
    "4D AC KC 8D 6D 4C 2D KH 2C JD",
    "2C 9H 2D AH 3H 6D 9C 7D TC KS",
    "8C 3H KD 7C 5C 2S 4S 5H AS AH",
    "TH JD 4H KD 3H TC 5C 3S AC KH",
    "6D 7H AH 7S QC 6H 2D TD JD AS",
    "JH 5D 7H TC 9S 7D JC AS 5S KH",
    "2H 8C AD TH 6H QD KD 9H 6S 6C",
    "QH KC 9D 4D 3S JS JH 4H 2C 9H",
    "TC 7H KH 4H JC 7D 9S 3H QS 7S",
    "AD 7D JH 6C 7H 4H 3S 3H 4D QH",
    "JD 2H 5C AS 6C QC 4D 3C TC JH",
    "AC JD 3H 6H 4C JC AD 7D 7H 9H",
    "4H TC TS 2C 8C 6S KS 2H JD 9S",
    "4C 3H QS QC 9S 9H 6D KC 9D 9C",
    "5C AD 8C 2C QH TH QD JC 8D 8H",
    "QC 2C 2S QD 9C 4D 3S 8D JH QS",
    "9D 3S 2C 7S 7C JC TD 3C TC 9H",
    "3C TS 8H 5C 4C 2C 6S 8D 7C 4H",
    "KS 7H 2H TC 4H 2C 3S AS AH QS",
    "8C 2D 2H 2C 4S 4C 6S 7D 5S 3S",
    "TH QC 5D TD 3C QS KD KC KS AS",
    "4D AH KD 9H KS 5C 4C 6H JC 7S",
    "KC 4H 5C QS TC 2H JC 9S AH QH",
    "4S 9H 3H 5H 3C QD 2H QC JH 8H",
    "5D AS 7H 2C 3D JH 6H 4C 6S 7D",
    "9C JD 9H AH JS 8S QH 3H KS 8H",
    "3S AC QC TS 4D AD 3D AH 8S 9H",
    "7H 3H QS 9C 9S 5H JH JS AH AC",
    "8D 3C JD 2H AC 9C 7H 5S 4D 8H",
    "7C JH 9H 6C JS 9S 7H 8C 9D 4H",
    "2D AS 9S 6H 4D JS JH 9H AD QD",
    "6H 7S JH KH AH 7H TD 5S 6S 2C",
    "8H JH 6S 5H 5S 9D TC 4C QC 9S",
    "7D 2C KD 3H 5H AS QD 7H JS 4D",
    "TS QH 6C 8H TH 5H 3C 3H 9C 9D",
    "AD KH JS 5D 3H AS AC 9S 5C KC",
    "2C KH 8C JC QS 6D AH 2D KC TC",
    "9D 3H 2S 7C 4D 6D KH KS 8D 7D",
    "9H 2S TC JH AC QC 3H 5S 3S 8H",
    "3S AS KD 8H 4C 3H 7C JH QH TS",
    "7S 6D 7H 9D JH 4C 3D 3S 6C AS",
    "4S 2H 2C 4C 8S 5H KC 8C QC QD",
    "3H 3S 6C QS QC 2D 6S 5D 2C 9D",
    "2H 8D JH 2S 3H 2D 6C 5C 7S AD",
    "9H JS 5D QH 8S TS 2H 7S 6S AD",
    "6D QC 9S 7H 5H 5C 7D KC JD 4H",
    "QC 5S 9H 9C 4D 6S KS 2S 4C 7C",
    "9H 7C 4H 8D 3S 6H 5C 8H JS 7S",
    "2D 6H JS TD 4H 4D JC TH 5H KC",
    "AC 7C 8D TH 3H 9S 2D 4C KC 4D",
    "KD QS 9C 7S 3D KS AD TS 4C 4H",
    "QH 9C 8H 2S 7D KS 7H 5D KD 4C",
    "9C 2S 2H JC 6S 6C TC QC JH 5C",
    "7S AC 8H KC 8S 6H QS JC 3D 6S",
    "JS 2D JH 8C 4S 6H 8H 6D 5D AD",
    "6H 7D 2S 4H 9H 7C AS AC 8H 5S",
    "3C JS 4S 6D 5H 2S QH 6S 9C 2C",
    "3D 5S 6S 9S 4C QS 8D QD 8S TC",
    "9C 3D AH 9H 5S 2C 7D AD JC 3S",
    "7H TC AS 3C 6S 6D 7S KH KC 9H",
    "3S TC 8H 6S 5H JH 8C 7D AC 2S",
    "QD 9D 9C 3S JC 8C KS 8H 5D 4D",
    "JS AH JD 6D 9D 8C 9H 9S 8H 3H",
    "2D 6S 4C 4D 8S AD 4S TC AH 9H",
    "TS AC QC TH KC 6D 4H 7S 8C 2H",
    "3C QD JS 9D 5S JC AH 2H TS 9H",
    "3H 4D QH 5D 9C 5H 7D 4S JC 3S",
    "8S TH 3H 7C 2H JD JS TS AC 8D",
    "9C 2H TD KC JD 2S 8C 5S AD 2C",
    "3D KD 7C 5H 4D QH QD TC 6H 7D",
    "7H 2C KC 5S KD 6H AH QC 7S QH",
    "6H 5C AC 5H 2C 9C 2D 7C TD 2S",
    "4D 9D AH 3D 7C JD 4H 8C 4C KS",
    "TH 3C JS QH 8H 4C AS 3D QS QC",
    "4D 7S 5H JH 6D 7D 6H JS KH 3C",
    "QD 8S 7D 2H 2C 7C JC 2S 5H 8C",
    "QH 8S 9D TC 2H AD 7C 8D QD 6S",
    "3S 7C AD 9H 2H 9S JD TS 4C 2D",
    "3S AS 4H QC 2C 8H 8S 7S TD TC",
    "JH TH TD 3S 4D 4H 5S 5D QS 2C",
    "8C QD QH TC 6D 4S 9S 9D 4H QC",
    "8C JS 9D 6H JD 3H AD 6S TD QC",
    "KC 8S 3D 7C TD 7D 8D 9H 4S 3S",
    "6C 4S 3D 9D KD TC KC KS AC 5S",
    "7C 6S QH 3D JS KD 6H 6D 2D 8C",
    "JD 2S 5S 4H 8S AC 2D 6S TS 5C",
    "5H 8C 5S 3C 4S 3D 7C 8D AS 3H",
    "AS TS 7C 3H AD 7D JC QS 6C 6H",
    "3S 9S 4C AC QH 5H 5D 9H TS 4H",
    "6C 5C 7H 7S TD AD JD 5S 2H 2S",
    "7D 6C KC 3S JD 8D 8S TS QS KH",
    "8S QS 8D 6C TH AC AH 2C 8H 9S",
    "7H TD KH QH 8S 3D 4D AH JD AS",
    "TS 3D 2H JC 2S JH KH 6C QC JS",
    "KC TH 2D 6H 7S 2S TC 8C 9D QS",
    "3C 9D 6S KH 8H 6D 5D TH 2C 2H",
    "6H TC 7D AD 4D 8S TS 9H TD 7S",
    "JS 6D JD JC 2H AC 6C 3D KH 8D",
    "KH JD 9S 5D 4H 4C 3H 7S QS 5C",
    "4H JD 5D 3S 3C 4D KH QH QS 7S",
    "JD TS 8S QD AH 4C 6H 3S 5S 2C",
    "QS 3D JD AS 8D TH 7C 6S QC KS",
    "7S 2H 8C QC 7H AC 6D 2D TH KH",
    "5S 6C 7H KH 7D AH 8C 5C 7S 3D",
    "3C KD AD 7D 6C 4D KS 2D 8C 4S",
    "7C 8D 5S 2D 2S AH AD 2C 9D TD",
    "3C AD 4S KS JH 7C 5C 8C 9C TH",
    "AS TD 4D 7C JD 8C QH 3C 5H 9S",
    "3H 9C 8S 9S 6S QD KS AH 5H JH",
    "QC 9C 5S 4H 2H TD 7D AS 8C 9D",
    "8C 2C 9D KD TC 7S 3D KH QC 3C",
    "4D AS 4C QS 5S 9D 6S JD QH KS",
    "6D AH 6C 4C 5H TS 9H 7D 3D 5S",
    "QS JD 7C 8D 9C AC 3S 6S 6C KH",
    "8H JH 5D 9S 6D AS 6S 3S QC 7H",
    "QD AD 5C JH 2H AH 4H AS KC 2C",
    "JH 9C 2C 6H 2D JS 5D 9H KC 6D",
    "7D 9D KD TH 3H AS 6S QC 6H AD",
    "JD 4H 7D KC 3H JS 3C TH 3D QS",
    "4C 3H 8C QD 5H 6H AS 8H AD JD",
    "TH 8S KD 5D QC 7D JS 5S 5H TS",
    "7D KC 9D QS 3H 3C 6D TS 7S AH",
    "7C 4H 7H AH QC AC 4D 5D 6D TH",
    "3C 4H 2S KD 8H 5H JH TC 6C JD",
    "4S 8C 3D 4H JS TD 7S JH QS KD",
    "7C QC KD 4D 7H 6S AD TD TC KH",
    "5H 9H KC 3H 4D 3D AD 6S QD 6H",
    "TH 7C 6H TS QH 5S 2C KC TD 6S",
    "7C 4D 5S JD JH 7D AC KD KH 4H",
    "7D 6C 8D 8H 5C JH 8S QD TH JD",
    "8D 7D 6C 7C 9D KD AS 5C QH JH",
    "9S 2C 8C 3C 4C KS JH 2D 8D 4H",
    "7S 6C JH KH 8H 3H 9D 2D AH 6D",
    "4D TC 9C 8D 7H TD KS TH KD 3C",
    "JD 9H 8D QD AS KD 9D 2C 2S 9C",
    "8D 3H 5C 7H KS 5H QH 2D 8C 9H",
    "2D TH 6D QD 6C KC 3H 3S AD 4C",
    "4H 3H JS 9D 3C TC 5H QH QC JC",
    "3D 5C 6H 3S 3C JC 5S 7S 2S QH",
    "AC 5C 8C 4D 5D 4H 2S QD 3C 3H",
    "2C TD AH 9C KD JS 6S QD 4C QC",
    "QS 8C 3S 4H TC JS 3H 7C JC AD",
    "5H 4D 9C KS JC TD 9S TS 8S 9H",
    "QD TS 7D AS AC 2C TD 6H 8H AH",
    "6S AD 8C 4S 9H 8D 9D KH 8S 3C",
    "QS 4D 2D 7S KH JS JC AD 4C 3C",
    "QS 9S 7H KC TD TH 5H JS AC JH",
    "6D AC 2S QS 7C AS KS 6S KH 5S",
    "6D 8H KH 3C QS 2H 5C 9C 9D 6C",
    "JS 2C 4C 6H 7D JC AC QD TD 3H",
    "4H QC 8H JD 4C KD KS 5C KC 7S",
    "6D 2D 3H 2S QD 5S 7H AS TH 6S",
    "AS 6D 8D 2C 8S TD 8H QD JC AH",
    "9C 9H 2D TD QH 2H 5C TC 3D 8H",
    "KC 8S 3D KH 2S TS TC 6S 4D JH",
    "9H 9D QS AC KC 6H 5D 4D 8D AH",
    "9S 5C QS 4H 7C 7D 2H 8S AD JS",
    "3D AC 9S AS 2C 2D 2H 3H JC KH",
    "7H QH KH JD TC KS 5S 8H 4C 8D",
    "2H 7H 3S 2S 5H QS 3C AS 9H KD",
    "AD 3D JD 6H 5S 9C 6D AC 9S 3S",
    "3D 5D 9C 2D AC 4S 2S AD 6C 6S",
    "QC 4C 2D 3H 6S KC QH QD 2H JH",
    "QC 3C 8S 4D 9S 2H 5C 8H QS QD",
    "6D KD 6S 7H 3S KH 2H 5C JC 6C",
    "3S 9S TC 6S 8H 2D AD 7S 8S TS",
    "3C 6H 9C 3H 5C JC 8H QH TD QD",
    "3C JS QD 5D TD 2C KH 9H TH AS",
    "9S TC JD 3D 5C 5H AD QH 9H KC",
    "TC 7H 4H 8H 3H TD 6S AC 7C 2S",
    "QS 9D 5D 3C JC KS 4D 6C JH 2S",
    "9S 6S 3C 7H TS 4C KD 6D 3D 9C",
    "2D 9H AH AC 7H 2S JH 3S 7C QC",
    "QD 9H 3C 2H AC AS 8S KD 8C KH",
    "2D 7S TD TH 6D JD 8D 4D 2H 5S",
    "8S QH KD JD QS JH 4D KC 5H 3S",
    "3C KH QC 6D 8H 3S AH 7D TD 2D",
    "5S 9H QH 4S 6S 6C 6D TS TH 7S",
    "6C 4C 6D QS JS 9C TS 3H 8D 8S",
    "JS 5C 7S AS 2C AH 2H AD 5S TC",
    "KD 6C 9C 9D TS 2S JC 4H 2C QD",
    "QS 9H TC 3H KC KS 4H 3C AD TH",
    "KH 9C 2H KD 9D TC 7S KC JH 2D",
    "7C 3S KC AS 8C 5D 9C 9S QH 3H",
    "2D 8C TD 4C 2H QC 5D TC 2C 7D",
    "KS 4D 6C QH TD KH 5D 7C AD 8D",
    "2S 9S 8S 4C 8C 3D 6H QD 7C 7H",
    "6C 8S QH 5H TS 5C 3C 4S 2S 2H",
    "8S 6S 2H JC 3S 3H 9D 8C 2S 7H",
    "QC 2C 8H 9C AC JD 4C 4H 6S 3S",
    "3H 3S 7D 4C 9S 5H 8H JC 3D TC",
    "QH 2S 2D 9S KD QD 9H AD 6D 9C",
    "8D 2D KS 9S JC 4C JD KC 4S TH",
    "KH TS 6D 4D 5C KD 5H AS 9H AD",
    "QD JS 7C 6D 5D 5C TH 5H QH QS",
    "9D QH KH 5H JH 4C 4D TC TH 6C",
    "KH AS TS 9D KD 9C 7S 4D 8H 5S",
    "KH AS 2S 7D 9D 4C TS TH AH 7C",
    "KS 4D AC 8S 9S 8D TH QH 9D 5C",
    "5D 5C 8C QS TC 4C 3D 3S 2C 8D",
    "9D KS 2D 3C KC 4S 8C KH 6C JC",
    "8H AH 6H 7D 7S QD 3C 4C 6C KC",
    "3H 2C QH 8H AS 7D 4C 8C 4H KC",
    "QD 5S 4H 2C TD AH JH QH 4C 8S",
    "3H QS 5S JS 8H 2S 9H 9C 3S 2C",
    "6H TS 7S JC QD AC TD KC 5S 3H",
    "QH AS QS 7D JC KC 2C 4C 5C 5S",
    "QH 3D AS JS 4H 8D 7H JC 2S 9C",
    "5D 4D 2S 4S 9D 9C 2D QS 8H 7H",
    "6D 7H 3H JS TS AC 2D JH 7C 8S",
    "JH 5H KC 3C TC 5S 9H 4C 8H 9D",
    "8S KC 5H 9H AD KS 9D KH 8D AH",
    "JC 2H 9H KS 6S 3H QC 5H AH 9C",
    "5C KH 5S AD 6C JC 9H QC 9C TD",
    "5S 5D JC QH 2D KS 8H QS 2H TS",
    "JH 5H 5S AH 7H 3C 8S AS TD KH",
    "6H 3D JD 2C 4C KC 7S AH 6C JH",
    "4C KS 9D AD 7S KC 7D 8H 3S 9C",
    "7H 5C 5H 3C 8H QC 3D KH 6D JC",
    "2D 4H 5D 7D QC AD AH 9H QH 8H",
    "KD 8C JS 9D 3S 3C 2H 5D 6D 2S",
    "8S 6S TS 3C 6H 8D 5S 3H TD 6C",
    "KS 3D JH 9C 7C 9S QS 5S 4H 6H",
    "7S 6S TH 4S KC KD 3S JC JH KS",
    "7C 3C 2S 6D QH 2C 7S 5H 8H AH",
    "KC 8D QD 6D KH 5C 7H 9D 3D 9C",
    "6H 2D 8S JS 9S 2S 6D KC 7C TC",
    "KD 9C JH 7H KC 8S 2S 7S 3D 6H",
    "4H 9H 2D 4C 8H 7H 5S 8S 2H 8D",
    "AD 7C 3C 7S 5S 4D 9H 3D JC KH",
    "5D AS 7D 6D 9C JC 4C QH QS KH",
    "KD JD 7D 3D QS QC 8S 6D JS QD",
    "6S 8C 5S QH TH 9H AS AC 2C JD",
    "QC KS QH 7S 3C 4C 5C KC 5D AH",
    "6C 4H 9D AH 2C 3H KD 3D TS 5C",
    "TD 8S QS AS JS 3H KD AC 4H KS",
    "7D 5D TS 9H 4H 4C 9C 2H 8C QC",
    "2C 7D 9H 4D KS 4C QH AD KD JS",
    "QD AD AH KH 9D JS 9H JC KD JD",
    "8S 3C 4S TS 7S 4D 5C 2S 6H 7C",
    "JS 7S 5C KD 6D QH 8S TD 2H 6S",
    "QH 6C TC 6H TD 4C 9D 2H QC 8H",
    "3D TS 4D 2H 6H 6S 2C 7H 8S 6C",
    "9H 9D JD JH 3S AH 2C 6S 3H 8S",
    "2C QS 8C 5S 3H 2S 7D 3C AD 4S",
    "5C QC QH AS TS 4S 6S 4C 5H JS",
    "JH 5C TD 4C 6H JS KD KH QS 4H",
    "TC KH JC 4D 9H 9D 8D KC 3C 8H",
    "2H TC 8S AD 9S 4H TS 7H 2C 5C",
    "4H 2S 6C 5S KS AH 9C 7C 8H KD",
    "TS QH TD QS 3C JH AH 2C 8D 7D",
    "5D KC 3H 5S AC 4S 7H QS 4C 2H",
    "3D 7D QC KH JH 6D 6C TD TH KD",
    "5S 8D TH 6C 9D 7D KH 8C 9S 6D",
    "JD QS 7S QC 2S QH JC 4S KS 8D",
    "7S 5S 9S JD KD 9C JC AD 2D 7C",
    "4S 5H AH JH 9C 5D TD 7C 2D 6S",
    "KC 6C 7H 6S 9C QD 5S 4H KS TD",
    "6S 8D KS 2D TH TD 9H JD TS 3S",
    "KH JS 4H 5D 9D TC TD QC JD TS",
    "QS QD AC AD 4C 6S 2D AS 3H KC",
    "4C 7C 3C TD QS 9C KC AS 8D AD",
    "KC 7H QC 6D 8H 6S 5S AH 7S 8C",
    "3S AD 9H JC 6D JD AS KH 6S JH",
    "AD 3D TS KS 7H JH 2D JS QD AC",
    "9C JD 7C 6D TC 6H 6C JC 3D 3S",
    "QC KC 3S JC KD 2C 8D AH QS TS",
    "AS KD 3D JD 8H 7C 8C 5C QD 6C",
];

• Q.13 Large sum

• Q.16 Power digit sum

• Q.20 Factorial digit sum

• Q.4 Largest palindrome product

• Q.36 Double-base palindromes

fn merge_each_other(num: &mut Vec<u8>, rev: &mut Vec<u8>) {
    let mut carry = 0u8;
    rev.iter().zip(num.iter_mut()).for_each(|(&r, d)| {
        let s = r + *d + carry;
        *d = s % 10;
        carry = s / 10;
    });
    if carry != 0 {
        num.push(carry);
        rev.push(0);
    }
    num.iter()
        .rev()
        .zip(rev.iter_mut())
        .for_each(|(&d, r)| *r = d);
}

fn symmetric_digit_vector_pair(mut n: u32, num: &mut Vec<u8>, rev: &mut Vec<u8>) {
    num.clear();
    rev.clear();
    while n > 0 {
        let d = (n % 10) as u8;
        rev.push(d);
        n /= 10;
    }
    rev.iter().rev().for_each(|&d| num.push(d));
}

fn main() {
    let mut count = 0u32;
    let mut num = Vec::with_capacity(56);
    let mut rev = Vec::with_capacity(56);
    'next_num: for n in 10u32..10_000 {
        symmetric_digit_vector_pair(n, &mut num, &mut rev);
        for _ in 0..50 {
            merge_each_other(&mut num, &mut rev);
            if rev == num {
                continue 'next_num;
            }
        }
        count += 1;
    }

    println!("{}", count);
    assert_eq!(count, 249);
}

use std::collections::LinkedList;

fn merge_each_other(num: &mut LinkedList<u8>, rev: &mut LinkedList<u8>) {
    let mut carry = 0u8;
    rev.iter().zip(num.iter_mut()).for_each(|(&r, d)| {
        let s = r + *d + carry;
        *d = s % 10;
        carry = s / 10;
    });
    if carry != 0 {
        num.push_back(carry);
        rev.push_back(0);
    }
    num.iter()
        .rev()
        .zip(rev.iter_mut())
        .for_each(|(&d, r)| *r = d);
}

fn symmetric_digit_vector_pair(mut n: u32) -> (LinkedList<u8>, LinkedList<u8>) {
    let mut rev = LinkedList::new();
    while n > 0 {
        let d = (n % 10) as u8;
        rev.push_back(d);
        n /= 10;
    }
    let num = rev.iter().rev().map(|&d| d).collect::<LinkedList<u8>>();
    (num, rev)
}

fn main() {
    let mut count = 0u32;
    'next_num: for n in 10u32..10_000 {
        let (mut num, mut rev) = symmetric_digit_vector_pair(n);
        for _ in 0..50 {
            merge_each_other(&mut num, &mut rev);
            if rev == num {
                continue 'next_num;
            }
        }
        count += 1;
    }

    println!("{}", count);
    assert_eq!(count, 249);
}

• Q.16 Power digit sum

• Q.20 Factorial digit sum

• Q.15 Lattice paths

struct BigNum {
    _v: Vec<u64>,
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    fn new() -> Self {
        BigNum {
            _v: vec![],
        }
    }
    fn init(&mut self, base: u8) {
        self._v.clear();
        self._v.push(base as u64);
    }
    fn multiply(&mut self, n: u8) {
        let mut carry = 0u64;
        for con in self._v.iter_mut() {
            *con = *con * n as u64 + carry;
            if *con < Self::TEN_MIL {
                carry = 0;
                continue;
            }
            carry = *con / Self::TEN_MIL;
            *con %= Self::TEN_MIL;
        }
        if carry != 0 {
            self._v.push(carry);
        }
    }
    fn digit_sum(&self) -> u32 {
        let mut sum = 0u32;
        for &con in &self._v {
            let mut t = con;
            while t > 0 {
                sum += (t % 10) as u32;
                t /= 10;
            }
        }
        sum
    }
}

fn main() {
    let mut bignum = BigNum::new();
    let mut max = 0u32;
    for a in 2u8..100 {
        if a % 10 == 0 {
            continue;
        }
        bignum.init(a);
        for _ in 2u8..100 {
            bignum.multiply(a);
            max = std::cmp::max(max, bignum.digit_sum());
        }
    }

    println!("{}", max);
    assert_eq!(max, 972);
}

struct BigNum {
    _v: Vec<u64>,
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    fn new() -> Self {
        BigNum {
            _v: vec![],
        }
    }
    fn compute(&mut self, base: u8, exp: u8) {
        self._v.clear();
        self._v.push(1);
        for _ in 0..exp {
            self._multiply(base as u64);
        }
    }
    fn _multiply(&mut self, n: u64) {
        let mut carry = 0u64;
        for con in self._v.iter_mut() {
            *con = *con * n + carry;
            if *con < Self::TEN_MIL {
                carry = 0;
                continue;
            }
            carry = *con / Self::TEN_MIL;
            *con %= Self::TEN_MIL;
        }
        if carry != 0 {
            self._v.push(carry);
        }
    }
    fn digit_sum(&self) -> u32 {
        let mut sum = 0u32;
        for &con in &self._v {
            let mut t = con;
            while t > 0 {
                sum += (t % 10) as u32;
                t /= 10;
            }
        }
        sum
    }
}

fn main() {
    let mut bignum = BigNum::new();
    let mut max = 0u32;
    for a in 2u8..100 {
        if a % 10 == 0 {
            continue;
        }
        for b in 2u8..100 {
            bignum.compute(a, b);
            max = std::cmp::max(max, bignum.digit_sum());
        }
    }

    println!("{}", max);
    assert_eq!(max, 972);
}

• Q.5 Smallest multiple
• Q.26 Reciprocal cycles

struct Fraction {
    deno_prev: u64,
    deno: u64,
    nume: u64,
    n: u32,
}

impl Fraction {
    fn new() -> Self {
        let deno_prev = 2u64;
        let deno = 5u64;
        Self {
            deno_prev,
            deno,
            nume: deno_prev + deno,
            n: 2,
        }
    }
    fn increment(&mut self) {
        self.n += 1;
        self.deno_prev = self.deno;
        self.deno += self.nume;
        self.nume = self.deno_prev + self.deno;
        const THRESHOLD: u64 = {
            let mut threshold = 1u64;
            while threshold < u64::MAX / 100 {
                threshold *= 10;
            }
            threshold
        };
        if self.deno > THRESHOLD && self.nume > THRESHOLD {
            self.deno /= 10;
            self.nume /= 10;
        }
    }
    fn has_numerator_more_digits(&self) -> bool {
        let mut n = self.nume;
        let mut d = self.deno;
        while n > 0 && d > 0 {
            n /= 10;
            d /= 10;
        }
        n > d
    }
}

fn main() {
    let mut count = 0u32;
    let mut frac = Fraction::new();
    while {
        if frac.has_numerator_more_digits() {
            count += 1;
        }
        frac.increment();
        frac.n <= 1000
    } {}

    println!("{}", count);
    assert_eq!(count, 153);
}

• Q.13 Large sum
• Q.16 Power digit sum

#[derive(Clone)]
struct BigNum {
    v: Vec<u64>,
}

impl BigNum {
    const TEN_MIL: u64 = 10_000_000_000;
    fn new(n: u8) -> Self {
        Self { v: vec![n as u64] }
    }
    fn merge(&mut self, page: usize, n: u64, carry: &mut u64) {
        if self.v.get(page).is_none() {
            self.v.push(0u64)
        }
        if let Some(con) = self.v.get_mut(page) {
            *con += n + *carry;
            if *con < Self::TEN_MIL {
                *carry = 0;
                return;
            }
            *carry = 1;
            *con -= Self::TEN_MIL;
        }
    }
    fn double(&mut self) -> &Self {
        let mut carry = 0u64;
        for con in self.v.iter_mut() {
            *con *= 2;
            *con += carry;
            if *con < Self::TEN_MIL {
                carry = 0;
                continue;
            }
            carry = 1;
            *con -= Self::TEN_MIL;
        }
        if carry != 0 {
            self.v.push(1u64);
        }
        self
    }
    fn add(&mut self, b: &BigNum) {
        let mut p = 0usize;
        let mut carry = 0u64;
        let mut ite = b.v.iter();
        while let Some(n) = ite.next() {
            self.merge(p, *n, &mut carry);
            p += 1;
        }
        while carry != 0 {
            self.merge(p, 0, &mut carry);
            p += 1;
        }
    }
}

struct Fraction {
    deno: BigNum,
    nume: BigNum,
    n: u32,
}

impl Fraction {
    fn new() -> Self {
        Self {
            deno: BigNum::new(5),
            nume: BigNum::new(7),
            n: 2,
        }
    }
    fn increment(&mut self) {
        self.n += 1;
        let t = self.nume.clone();
        self.nume.add(self.deno.clone().double());
        self.deno.add(&t);
    }
    fn has_numerator_more_digits(&self) -> bool {
        if self.nume.v.len() != self.deno.v.len() {
            return self.nume.v.len() > self.deno.v.len();
        }
        let mut n = *self.nume.v.last().expect("BigNum must have a container");
        let mut d = *self.deno.v.last().expect("BigNum must have a container");
        while n > 0 && d > 0 {
            n /= 10;
            d /= 10;
        }
        n > d
    }
}

fn main() {
    let mut count = 0u32;
    let mut frac = Fraction::new();
    while {
        if frac.has_numerator_more_digits() {
            count += 1;
        }
        frac.increment();
        frac.n <= 1000
    } {}

    println!("{}", count);
    assert_eq!(count, 153);
}

• Q.2 Even Fibonacci numbers

• Convergence to √2, stackexchange

• How to solve linear recurrence relations with constant coefficients, stackexchange

• https://projecteuler.net/action=quote;post_id=10616

fn main() {
    let r1 = 1f64 + 2f64.sqrt();
    let r2 = 1f64 - 2f64.sqrt();
    let deno_c = 1.5f64 * 2f64.log10();
    let nume_c = 2f64.log10();
    let log10_r1 = r1.log10();
    let r2_over_r1 = r2 / r1;

    let mut count = 0u32;
    let mut pow = r2_over_r1.clone();
    for n in 2u32..=1001 {
        pow *= r2_over_r1;
        let nlog10r1 = n as f64 * log10_r1;
        let deno_digit = (nlog10r1 + (1f64 - pow).log10() - deno_c) as u32;
        let nume_digit = (nlog10r1 + (1f64 + pow).log10() - nume_c) as u32;
        if nume_digit > deno_digit {
            count += 1;
        }
    }

    println!("{}", count);
    assert_eq!(count, 153);
}

fn main() {
    let r1 = 1f64 + 2f64.sqrt();
    let deno_c = 1.5f64 * 2f64.log10();
    let nume_c = 2f64.log10();
    let log10_r1 = r1.log10();

    let mut count = 0u32;
    for n in 2u32..=1001 {
        let nlog10r1 = n as f64 * log10_r1;
        let deno_digit = (nlog10r1 - deno_c) as u32;
        let nume_digit = (nlog10r1 - nume_c) as u32;
        if nume_digit > deno_digit {
            count += 1;
        }
    }

    println!("{}", count);
    assert_eq!(count, 153);
}

37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18  5  4  3 12 29
40 19  6  1  2 11 28
41 20  7  8  9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49

• Q.28 Number spiral diagonals

fn is_prime(n: u32) -> bool {
    if n < 2 {
        return false;
    }
    if n == 2 || n == 3 || n == 5 {
        return true;
    }
    for d in &[2, 3, 5] {
        if n % *d == 0 {
            return false;
        }
    }
    let side = (n as f32).sqrt() as u32;
    let mut d = 5;
    for &i in [2, 4].iter().cycle() {
        d += i;
        if d > side {
            break;
        }
        if n % d == 0 {
            return false;
        }
    }
    true
}

struct Spiral {
    n: u32,
    diagonal_area: u32,
    primes: u32,
}

impl Spiral {
    fn increment(&mut self) {
        self.n += 1;
        self.diagonal_area += 4;
        self.primes += self.prime_corners();
    }
    fn prime_corners(&self) -> u32 {
        let square = (2 * self.n + 1) * (2 * self.n + 1);
        (1u32..=3)
            .map(|i| square - 2 * self.n * i)
            .filter(|&n| is_prime(n))
            .count() as u32
    }
}

fn main() {
   let mut spiral = Spiral {
        n: 0,
        diagonal_area: 1,
        primes: 0,
    };
    while {
        spiral.increment();
        spiral.primes * 10 >= spiral.diagonal_area
    } {}
    let side = 2 * spiral.n + 1;

    println!("{}", side);
    assert_eq!(side, 26241)
}

• Q.26 Reciprocal cycles
• Q.50 Consecutive prime sum
• cp-algorithms.com/algebra/primality_tests

The LCG is still good enough for simple tasks like Miller-Rabin primality test, or FreeCell deals. (Linear congruential generator, rosettacode.org)

use std::time::{SystemTime, UNIX_EPOCH};

mod index {
    pub struct Index {
        pub i: usize,
        f: u8,
    }

    impl Index {
        pub fn increment(&mut self) {
            self.i += 2 << self.f;
            self.f ^= 1;
        }
        pub fn new() -> Self {
            Self { i: 5, f: 0 }
        }
    }
}

mod sieve {
    pub struct Sieve {
        sieve: [bool; 100_001],
        index: super::index::Index,
    }

    impl Sieve {
        pub fn new() -> Self {
            let mut s = Self {
                sieve: [true; 100_001],
                index: super::index::Index::new(),
            };
            s.init();
            s
        }
        pub fn sieve_len(&self) -> u32 {
            self.sieve.len() as u32
        }
        fn init(&mut self) {
            let side = ((self.sieve.len() - 1) as f32).sqrt() as usize;
            while self.index.i <= side {
                if self.sieve[self.index.i] {
                    let p = self.index.i;
                    (p * p..self.sieve.len())
                        .step_by(p)
                        .for_each(|i| self.sieve[i] = false);
                }
                self.index.increment();
            }
        }
        pub fn is_prime(&self, n: u32) -> bool {
            assert!(n < self.sieve.len() as u32);
            if n < 2 {
                return false;
            }
            if n % 2 == 0 {
                return n == 2;
            }
            if n % 3 == 0 {
                return n == 3;
            }
            return self.sieve[n as usize];
        }
    }
}

mod rand {
    pub struct MinStdRand {
        state: u64,
    }

    impl MinStdRand {
        const M: u64 = 2147483647;
        const A: u64 = 48271;
        const MAX: u64 = 2147483646;
        pub fn new(seed: u32) -> Self {
            Self { state: seed as u64 }
        }
        pub fn next(&mut self, partition: u32) -> u32 {
            let p = partition as u64;
            assert!(p > 0 && p <= Self::MAX);
            self.state = Self::A * self.state % Self::M;
            loop {
                let n = self.state * p / Self::MAX;
                if n < p {
                    return n as u32;
                }
            }
        }
    }
}

fn mod_pow(a: u32, exp: u32, m: u32) -> u32 {
    let (mut a, mut exp, m) = (a as u64, exp as u64, m as u64);
    if m == 1 {
        return 0;
    }
    if exp == 0 {
        return 1;
    }
    let mut result = 1;
    a %= m;
    loop {
        if exp % 2 == 1 {
            result = result * a % m;
        }
        exp >>= 1;
        if exp == 0 {
            break;
        }
        a = a * a % m;
    }
    result as u32
}

/// finds the k*2^e form of given n 
fn coefficient_and_exponent_of_two(mut n: u32) -> (u32, u32) {
    let mut exp = 0u32;
    while n % 2 == 0 {
        n /= 2;
        exp += 1;
    }
    (n, exp)
}

fn is_probable_prime(n: u32, rand: &mut rand::MinStdRand) -> bool {
    if n == 1 {
        return false;
    }
    if n % 2 == 0 {
        return n == 2;
    }
    let (d, s) = coefficient_and_exponent_of_two(n - 1); 
    'next_trial: for _ in 0..3 {
        // 2 <= a < n
        let a = 2 + rand.next(n - 2);
        let mut x = mod_pow(a, d, n);
        if x == 1 || x == n - 1 {
            continue 'next_trial;
        }
        for _ in 1..s {
            x = (x as u64 * x as u64 % n as u64) as u32;
            if x == n - 1 {
                continue 'next_trial;
            }
        }
        return false;
    }
    true
}

struct Spiral {
    n: u32,
    diagonal_area: u32,
    primes: u32,
    sieve: sieve::Sieve,
    rand: rand::MinStdRand,
}

impl Spiral {
    fn increment(&mut self) {
        self.n += 1;
        self.diagonal_area += 4;
        self.primes += self.prime_corners();
    }
    fn prime_corners(&mut self) -> u32 {
        let square = (2 * self.n + 1) * (2 * self.n + 1);
        let n = self.n.clone();
        (1u32..=3)
            .map(|i| square - 2 * n * i)
            .filter(|&n| {
                if n < self.sieve.sieve_len() {
                    self.sieve.is_prime(n)
                } else {
                    is_probable_prime(n, &mut self.rand)
                }
            })
            .count() as u32
    }
}

fn main() {
    let seed = SystemTime::now()
        .duration_since(UNIX_EPOCH)
        .unwrap()
        .subsec_nanos();
    let mut spiral = Spiral {
        n: 0,
        diagonal_area: 1,
        primes: 0,
        sieve: sieve::Sieve::new(),
        rand: rand::MinStdRand::new(seed),
    };
    while {
        spiral.increment();
        spiral.primes * 10 >= spiral.diagonal_area
    } {}
    let side = 2 * spiral.n + 1;

    println!("{}", side);
    assert_eq!(side, 26241)
}

fn get_most_frequent_value(position: usize) -> u8 {
    let mut freq = [0u8; 256];
    for i in (position..).step_by(3) {
        if i > ENC.len() - 1 {
            break;
        }
        freq[ENC[i] as usize] += 1;
    }
    freq.iter()
        .enumerate()
        .reduce(|a, b| if a.1 > b.1 { a } else { b })
        .map(|(i, _)| i as u8)
        .expect("freq array's length must be > 0.")
}

fn get_key_from_space(enc: u8) -> u8 {
    let space = ' ' as u8;
    for c in 'a'..='z' {
        if c as u8 ^ enc == space {
            return c as u8;
        }
    }
    unreachable!();
}

fn decrypt(dec: &mut [u8], position: usize, key: u8) {
    for i in (position..).step_by(3) {
        if i > ENC.len() - 1 {
            break;
        }
        dec[i] = ENC[i] ^ key;
    }
}

fn main() {
    let mut dec = vec![0; ENC.len()];
    for i in 0usize..3 {
        let enc = get_most_frequent_value(i);
        let key = get_key_from_space(enc);
        decrypt(&mut dec, i, key);
    }
    let ans = dec.iter().map(|&v| v as u32).sum::<u32>();
    println!("{}", ans);
    assert_eq!(ans, 129448);
    println!("{}", String::from_utf8(dec).unwrap());
}

const ENC: [u8; 1455] = [
    36, 22, 80, 0, 0, 4, 23, 25, 19, 17, 88, 4, 4, 19, 21, 11, 88, 22, 23, 23, 29, 69, 12, 24, 0,
    88, 25, 11, 12, 2, 10, 28, 5, 6, 12, 25, 10, 22, 80, 10, 30, 80, 10, 22, 21, 69, 23, 22, 69,
    61, 5, 9, 29, 2, 66, 11, 80, 8, 23, 3, 17, 88, 19, 0, 20, 21, 7, 10, 17, 17, 29, 20, 69, 8, 17,
    21, 29, 2, 22, 84, 80, 71, 60, 21, 69, 11, 5, 8, 21, 25, 22, 88, 3, 0, 10, 25, 0, 10, 5, 8, 88,
    2, 0, 27, 25, 21, 10, 31, 6, 25, 2, 16, 21, 82, 69, 35, 63, 11, 88, 4, 13, 29, 80, 22, 13, 29,
    22, 88, 31, 3, 88, 3, 0, 10, 25, 0, 11, 80, 10, 30, 80, 23, 29, 19, 12, 8, 2, 10, 27, 17, 9,
    11, 45, 95, 88, 57, 69, 16, 17, 19, 29, 80, 23, 29, 19, 0, 22, 4, 9, 1, 80, 3, 23, 5, 11, 28,
    92, 69, 9, 5, 12, 12, 21, 69, 13, 30, 0, 0, 0, 0, 27, 4, 0, 28, 28, 28, 84, 80, 4, 22, 80, 0,
    20, 21, 2, 25, 30, 17, 88, 21, 29, 8, 2, 0, 11, 3, 12, 23, 30, 69, 30, 31, 23, 88, 4, 13, 29,
    80, 0, 22, 4, 12, 10, 21, 69, 11, 5, 8, 88, 31, 3, 88, 4, 13, 17, 3, 69, 11, 21, 23, 17, 21,
    22, 88, 65, 69, 83, 80, 84, 87, 68, 69, 83, 80, 84, 87, 73, 69, 83, 80, 84, 87, 65, 83, 88, 91,
    69, 29, 4, 6, 86, 92, 69, 15, 24, 12, 27, 24, 69, 28, 21, 21, 29, 30, 1, 11, 80, 10, 22, 80,
    17, 16, 21, 69, 9, 5, 4, 28, 2, 4, 12, 5, 23, 29, 80, 10, 30, 80, 17, 16, 21, 69, 27, 25, 23,
    27, 28, 0, 84, 80, 22, 23, 80, 17, 16, 17, 17, 88, 25, 3, 88, 4, 13, 29, 80, 17, 10, 5, 0, 88,
    3, 16, 21, 80, 10, 30, 80, 17, 16, 25, 22, 88, 3, 0, 10, 25, 0, 11, 80, 12, 11, 80, 10, 26, 4,
    4, 17, 30, 0, 28, 92, 69, 30, 2, 10, 21, 80, 12, 12, 80, 4, 12, 80, 10, 22, 19, 0, 88, 4, 13,
    29, 80, 20, 13, 17, 1, 10, 17, 17, 13, 2, 0, 88, 31, 3, 88, 4, 13, 29, 80, 6, 17, 2, 6, 20, 21,
    69, 30, 31, 9, 20, 31, 18, 11, 94, 69, 54, 17, 8, 29, 28, 28, 84, 80, 44, 88, 24, 4, 14, 21,
    69, 30, 31, 16, 22, 20, 69, 12, 24, 4, 12, 80, 17, 16, 21, 69, 11, 5, 8, 88, 31, 3, 88, 4, 13,
    17, 3, 69, 11, 21, 23, 17, 21, 22, 88, 25, 22, 88, 17, 69, 11, 25, 29, 12, 24, 69, 8, 17, 23,
    12, 80, 10, 30, 80, 17, 16, 21, 69, 11, 1, 16, 25, 2, 0, 88, 31, 3, 88, 4, 13, 29, 80, 21, 29,
    2, 12, 21, 21, 17, 29, 2, 69, 23, 22, 69, 12, 24, 0, 88, 19, 12, 10, 19, 9, 29, 80, 18, 16, 31,
    22, 29, 80, 1, 17, 17, 8, 29, 4, 0, 10, 80, 12, 11, 80, 84, 67, 80, 10, 10, 80, 7, 1, 80, 21,
    13, 4, 17, 17, 30, 2, 88, 4, 13, 29, 80, 22, 13, 29, 69, 23, 22, 69, 12, 24, 12, 11, 80, 22,
    29, 2, 12, 29, 3, 69, 29, 1, 16, 25, 28, 69, 12, 31, 69, 11, 92, 69, 17, 4, 69, 16, 17, 22, 88,
    4, 13, 29, 80, 23, 25, 4, 12, 23, 80, 22, 9, 2, 17, 80, 70, 76, 88, 29, 16, 20, 4, 12, 8, 28,
    12, 29, 20, 69, 26, 9, 69, 11, 80, 17, 23, 80, 84, 88, 31, 3, 88, 4, 13, 29, 80, 21, 29, 2, 12,
    21, 21, 17, 29, 2, 69, 12, 31, 69, 12, 24, 0, 88, 20, 12, 25, 29, 0, 12, 21, 23, 86, 80, 44,
    88, 7, 12, 20, 28, 69, 11, 31, 10, 22, 80, 22, 16, 31, 18, 88, 4, 13, 25, 4, 69, 12, 24, 0, 88,
    3, 16, 21, 80, 10, 30, 80, 17, 16, 25, 22, 88, 3, 0, 10, 25, 0, 11, 80, 17, 23, 80, 7, 29, 80,
    4, 8, 0, 23, 23, 8, 12, 21, 17, 17, 29, 28, 28, 88, 65, 75, 78, 68, 81, 65, 67, 81, 72, 70, 83,
    64, 68, 87, 74, 70, 81, 75, 70, 81, 67, 80, 4, 22, 20, 69, 30, 2, 10, 21, 80, 8, 13, 28, 17,
    17, 0, 9, 1, 25, 11, 31, 80, 17, 16, 25, 22, 88, 30, 16, 21, 18, 0, 10, 80, 7, 1, 80, 22, 17,
    8, 73, 88, 17, 11, 28, 80, 17, 16, 21, 11, 88, 4, 4, 19, 25, 11, 31, 80, 17, 16, 21, 69, 11, 1,
    16, 25, 2, 0, 88, 2, 10, 23, 4, 73, 88, 4, 13, 29, 80, 11, 13, 29, 7, 29, 2, 69, 75, 94, 84,
    76, 65, 80, 65, 66, 83, 77, 67, 80, 64, 73, 82, 65, 67, 87, 75, 72, 69, 17, 3, 69, 17, 30, 1,
    29, 21, 1, 88, 0, 23, 23, 20, 16, 27, 21, 1, 84, 80, 18, 16, 25, 6, 16, 80, 0, 0, 0, 23, 29, 3,
    22, 29, 3, 69, 12, 24, 0, 88, 0, 0, 10, 25, 8, 29, 4, 0, 10, 80, 10, 30, 80, 4, 88, 19, 12, 10,
    19, 9, 29, 80, 18, 16, 31, 22, 29, 80, 1, 17, 17, 8, 29, 4, 0, 10, 80, 12, 11, 80, 84, 86, 80,
    35, 23, 28, 9, 23, 7, 12, 22, 23, 69, 25, 23, 4, 17, 30, 69, 12, 24, 0, 88, 3, 4, 21, 21, 69,
    11, 4, 0, 8, 3, 69, 26, 9, 69, 15, 24, 12, 27, 24, 69, 49, 80, 13, 25, 20, 69, 25, 2, 23, 17,
    6, 0, 28, 80, 4, 12, 80, 17, 16, 25, 22, 88, 3, 16, 21, 92, 69, 49, 80, 13, 25, 6, 0, 88, 20,
    12, 11, 19, 10, 14, 21, 23, 29, 20, 69, 12, 24, 4, 12, 80, 17, 16, 21, 69, 11, 5, 8, 88, 31, 3,
    88, 4, 13, 29, 80, 22, 29, 2, 12, 29, 3, 69, 73, 80, 78, 88, 65, 74, 73, 70, 69, 83, 80, 84,
    87, 72, 84, 88, 91, 69, 73, 95, 87, 77, 70, 69, 83, 80, 84, 87, 70, 87, 77, 80, 78, 88, 21, 17,
    27, 94, 69, 25, 28, 22, 23, 80, 1, 29, 0, 0, 22, 20, 22, 88, 31, 11, 88, 4, 13, 29, 80, 20, 13,
    17, 1, 10, 17, 17, 13, 2, 0, 88, 31, 3, 88, 4, 13, 29, 80, 6, 17, 2, 6, 20, 21, 75, 88, 62, 4,
    21, 21, 9, 1, 92, 69, 12, 24, 0, 88, 3, 16, 21, 80, 10, 30, 80, 17, 16, 25, 22, 88, 29, 16, 20,
    4, 12, 8, 28, 12, 29, 20, 69, 26, 9, 69, 65, 64, 69, 31, 25, 19, 29, 3, 69, 12, 24, 0, 88, 18,
    12, 9, 5, 4, 28, 2, 4, 12, 21, 69, 80, 22, 10, 13, 2, 17, 16, 80, 21, 23, 7, 0, 10, 89, 69, 23,
    22, 69, 12, 24, 0, 88, 19, 12, 10, 19, 16, 21, 22, 0, 10, 21, 11, 27, 21, 69, 23, 22, 69, 12,
    24, 0, 88, 0, 0, 10, 25, 8, 29, 4, 0, 10, 80, 10, 30, 80, 4, 88, 19, 12, 10, 19, 9, 29, 80, 18,
    16, 31, 22, 29, 80, 1, 17, 17, 8, 29, 4, 0, 10, 80, 12, 11, 80, 84, 86, 80, 36, 22, 20, 69, 26,
    9, 69, 11, 25, 8, 17, 28, 4, 10, 80, 23, 29, 17, 22, 23, 30, 12, 22, 23, 69, 49, 80, 13, 25, 6,
    0, 88, 28, 12, 19, 21, 18, 17, 3, 0, 88, 18, 0, 29, 30, 69, 25, 18, 9, 29, 80, 17, 23, 80, 1,
    29, 4, 0, 10, 29, 12, 22, 21, 69, 12, 24, 0, 88, 3, 16, 21, 3, 69, 23, 22, 69, 12, 24, 0, 88,
    3, 16, 26, 3, 0, 9, 5, 0, 22, 4, 69, 11, 21, 23, 17, 21, 22, 88, 25, 11, 88, 7, 13, 17, 19, 13,
    88, 4, 13, 29, 80, 0, 0, 0, 10, 22, 21, 11, 12, 3, 69, 25, 2, 0, 88, 21, 19, 29, 30, 69, 22, 5,
    8, 26, 21, 23, 11, 94,
];

Primes

• Q.37 Truncatable primes
• Q.58 Spiral primes

Recursion

• Q.31 Coin sums
• Q.41 Pandigital prime
• Q.43 Sub-string divisibility

use std::time::{SystemTime, UNIX_EPOCH};
use std::collections::HashMap;

fn concat(mut a: u32, b: u32) -> u32 {
    let mut t = b.clone();
    while t > 0 {
        a *= 10;
        t /= 10;
    }
    a + b
}

fn is_pair(a: u32, b: u32, sieve: &sieve::Sieve, rand: &mut rand::MinStdRand) -> bool {
    let ab = concat(a, b);
    let is_ab_prime = if ab < sieve.sieve_len() {
        sieve.is_prime(ab)
    } else {
        is_probable_prime(ab, rand)
    };
    if !is_ab_prime {
        return false;
    }
    let ba = concat(b, a);
    if ba < sieve.sieve_len() {
        sieve.is_prime(ba)
    } else {
        is_probable_prime(ba, rand)
    }
}

fn pairing(
    a: u32,
    primes: &[u32],
    sieve: &sieve::Sieve,
    rand: &mut rand::MinStdRand,
) -> Option<Vec<u32>> {
    let mut pairs: Option<Vec<u32>> = None;
    for &b in primes {
        if !is_pair(a, b, sieve, rand) {
            continue;
        }
        if let Some(vec) = pairs.as_mut() {
            vec.push(b);
        } else {
            pairs.insert(vec![b]);
        }
    }
    pairs
}

fn dig_to_bottom(
    candidates: &[u32],
    pair_table: &HashMap<u32, Vec<u32>>,
    drain: &[u32],
    angle: usize,
) -> Result<Vec<u32>, ()> {
    if angle == 1 {
        let set = std::iter::once(candidates.get(0).unwrap())
            .chain(drain.iter())
            .map(|&n| n)
            .collect::<Vec<u32>>();
        return Ok(set);
    }
    for p in candidates.iter() {
        let pairs = pair_table.get(p);
        let pairs = if pairs.is_none() {
            continue;
        } else {
            pairs.unwrap()
        };
        if pairs.len() < angle - 1 {
            continue;
        }
        let pairs = pairs
            .iter()
            .filter(|&e| candidates.binary_search(e).is_ok())
            .map(|e| *e)
            .collect::<Vec<u32>>();
        if pairs.len() < angle - 1 {
            continue;
        }
        let drain = std::iter::once(p)
            .chain(drain.iter())
            .map(|&n| n)
            .collect::<Vec<u32>>();
        let result = dig_to_bottom(&pairs, pair_table, &drain, angle - 1);
        if result.is_ok() {
            return result;
        }
    }
    Err(())
}

fn mod_pow(a: u32, exp: u32, m: u32) -> u32 {
    let (mut a, mut exp, m) = (a as u64, exp as u64, m as u64);
    if m == 1 {
        return 0;
    }
    if exp == 0 {
        return 1;
    }
    let mut result = 1;
    a %= m;
    loop {
        if exp % 2 == 1 {
            result = result * a % m;
        }
        exp >>= 1;
        if exp == 0 {
            break;
        }
        a = a * a % m;
    }
    result as u32
}

/// finds the k*2^e form of given n
fn coefficient_and_exponent_of_two(mut n: u32) -> (u32, u32) {
    let mut exp = 0u32;
    while n % 2 == 0 {
        n /= 2;
        exp += 1;
    }
    (n, exp)
}

fn is_probable_prime(n: u32, rand: &mut rand::MinStdRand) -> bool {
    if n == 1 {
        return false;
    }
    if n % 2 == 0 {
        return n == 2;
    }
    let (d, s) = coefficient_and_exponent_of_two(n - 1);
    'next_trial: for _ in 0..3 {
        let a = 2 + rand.next(n - 2);
        let mut x = mod_pow(a, d, n);
        if x == 1 || x == n - 1 {
            continue 'next_trial;
        }
        for _ in 1..s {
            x = (x as u64 * x as u64 % n as u64) as u32;
            if x == n - 1 {
                continue 'next_trial;
            }
        }
        return false;
    }
    true
}

mod index {
    pub struct Index {
        pub i: usize,
        f: u8,
    }

    impl Index {
        pub fn increment(&mut self) {
            self.i += 2 << self.f;
            self.f ^= 1;
        }
        pub fn new() -> Self {
            Self { i: 5, f: 0 }
        }
    }
}

mod sieve {
    pub struct Sieve {
        sieve: Vec<bool>,
        index: super::index::Index,
        primes: Vec<usize>,
        queue_cursor: usize,
    }

    impl Sieve {
        pub fn new(below: u32) -> Self {
            assert!(below > 4);
            let sieve = vec![true; below as usize];
            let mut s = Self {
                sieve: sieve,
                index: super::index::Index::new(),
                primes: vec![],
                queue_cursor: 0,
            };
            s.clean_sieve();
            s
        }
        pub fn sieve_len(&self) -> u32 {
            self.sieve.len() as u32
        }
        fn rule_out(&mut self, prime: usize) {
            for i in (prime * prime..self.sieve.len()).step_by(prime) {
                self.sieve[i] = false;
            }
        }
        fn rule_out_from_previous_position(&mut self, prime: usize, pp: usize) {
            use std::cmp::max;
            let begin = max((((pp - 1) / prime) + 1) * prime, prime * prime);
            for i in (begin..self.sieve.len()).step_by(prime) {
                self.sieve[i] = false;
            }
        }
        fn clean_sieve(&mut self) {
            let side = ((self.sieve.len() - 1) as f32).sqrt() as usize;
            while self.index.i <= side {
                if self.sieve[self.index.i] {
                    self.primes.push(self.index.i);
                    self.rule_out(self.index.i);
                }
                self.index.increment();
            }
            while self.index.i < self.sieve.len() {
                if self.sieve[self.index.i] {
                    self.primes.push(self.index.i);
                }
                self.index.increment();
            }
        }
        fn extend(&mut self) {
            let previous_len = self.sieve.len();
            self.sieve.extend(vec![true; previous_len]);
            for &p in &self.primes.clone() {
                self.rule_out_from_previous_position(p, previous_len);
            }
            self.clean_sieve();
        }
        pub fn next_prime(&mut self) -> u32 {
            loop {
                if self.queue_cursor == 0 {
                    self.queue_cursor += 1;
                    return 2;
                }
                if self.queue_cursor == 1 {
                    self.queue_cursor += 1;
                    return 3;
                }
                if self.queue_cursor - 2 < self.primes.len() {
                    self.queue_cursor += 1;
                    return self.primes[self.queue_cursor - 3] as u32;
                }
                self.extend();
            }
        }
        pub fn is_prime(&self, n: u32) -> bool {
            assert!(n < self.sieve.len() as u32);
            if n < 2 {
                return false;
            }
            if n % 2 == 0 {
                return n == 2;
            }
            if n % 3 == 0 {
                return n == 3;
            }
            return self.sieve[n as usize];
        }
    }
}

mod rand {
    pub struct MinStdRand {
        state: u64,
    }

    impl MinStdRand {
        const M: u64 = 2147483647;
        const A: u64 = 48271;
        const MAX: u64 = 2147483646;
        pub fn new(seed: u32) -> Self {
            Self { state: seed as u64 }
        }
        pub fn next(&mut self, partition: u32) -> u32 {
            let p = partition as u64;
            assert!(p > 0 && p <= Self::MAX);
            self.state = Self::A * self.state % Self::M;
            loop {
                let n = self.state * p / Self::MAX;
                if n < p {
                    return n as u32;
                }
            }
        }
    }
}

fn prime_graph(angle: usize) -> Vec<u32> {
    let mut primes = vec![];
    let mut sieve = sieve::Sieve::new(1000);
    let seed = SystemTime::now()
        .duration_since(UNIX_EPOCH)
        .unwrap()
        .subsec_nanos();
    let mut rand = rand::MinStdRand::new(seed);
    let mut pair_table: HashMap<u32, Vec<u32>> = HashMap::new();
    sieve.next_prime(); // discard 2
    loop {
        let p = sieve.next_prime();
        let pairs = pairing(p, &primes, &sieve, &mut rand);
        primes.push(p);
        let pairs = if pairs.is_none() {
            continue;
        } else {
            pairs.unwrap()
        };
        if pairs.len() < angle - 1 {
            pair_table.insert(p, pairs);
            continue;
        }
        if let Ok(ans) = dig_to_bottom(&pairs, &pair_table, &vec![p], angle - 1) {
            break ans;
        }
        pair_table.insert(p, pairs);
    }
} 

fn main() {
    {
        let ans = prime_graph(3);
        let sum = ans.iter().sum::<u32>();
        println!("{} {:?}", sum, ans);
        assert_eq!(sum, 107);
    }
    {
        let ans = prime_graph(4);
        let sum = ans.iter().sum::<u32>();
        println!("{} {:?}", sum, ans);
        assert_eq!(sum, 792);
    }
    {
        let ans = prime_graph(5);
        let sum = ans.iter().sum::<u32>();
        println!("{} {:?}", sum, ans);
        assert_eq!(sum, 26033);
    }
}

• Q.12 Highly divisible triangular number
• Q.42 Coded triangle numbers
• Q.44 Pentagon numbers
• Q.45 Triangular, pentagonal, and hexagonal

#[derive(Debug)]
struct PolyNum {
    left: u8,
    right: u8,
    side_ident: u8,
}

fn next(filter: u8, polynums: &[PolyNum], chain: &[&PolyNum]) -> Option<u32> {
    if filter == 0b11111100 {
        if chain[chain.len() - 1].right != chain[0].left {
            return None;
        }
        println!("{:#?}", chain);
        let sum = chain
            .iter()
            .map(|&pn| pn.left as u32 * 100 + pn.right as u32)
            .sum();
        return Some(sum);
    }
    let oks = polynums
        .iter()
        .filter(|&pn| pn.left == chain[chain.len() - 1].right)
        .filter(|&pn| pn.side_ident & filter == 0)
        .collect::<Vec<&PolyNum>>();
    for pn in oks {
        let chain = chain
            .iter()
            .map(|&p| p)
            .chain(std::iter::once(pn))
            .collect::<Vec<&PolyNum>>();
        let child = next(filter | pn.side_ident, polynums, &chain);
        if child.is_some() {
            return child;
        }
    }
    None
}

fn generate_four_digit_polygonal_numbers(side: u32) -> Vec<PolyNum> {
    let polygonal_number_genenerator_builder =
        |side: u32| move |n: u32| (side - 2) * n * (n - 1) / 2 + n;

    let gen = polygonal_number_genenerator_builder(side);
    let mut polynums = vec![];
    for n in 1u32.. {
        let x = gen(n);
        if x > 9999 {
            break;
        }
        if x < 1000 {
            continue;
        }
        polynums.push(PolyNum {
            left: (x / 100) as u8,
            right: (x % 100) as u8,
            side_ident: 1 << (side - 1),
        });
    }
    polynums
}

fn cyclical_figurate_numbers() -> u32 {
    let octs = generate_four_digit_polygonal_numbers(8);

    let mut polynums = vec![];
    for s in 3u32..=7 {
        polynums.extend(generate_four_digit_polygonal_numbers(s).into_iter());
    }

    for oct in &octs {
        if let Some(sum) = next(oct.side_ident, &polynums, &vec![oct]) {
            return sum;
        }
    }
    unreachable!();
}

fn main() {
   let ans = cyclical_figurate_numbers();
   println!("{}", ans);
   assert_eq!(ans, 28684);
}

use std::collections::HashMap;

fn freq(mut n: u64) -> u64 {
    let mut freq = 0u64;
    while n > 0 {
        freq += 0b000001 << ((n % 10) * 6);
        n /= 10;
    }
    freq
}

fn min(counts: &HashMap<u64, (u8, u16)>, count: u8) -> Option<&u16> {
    counts
        .iter()
        .filter(|(_, (c, _))| *c == count)
        .map(|(_, (_, n))| n)
        .min()
}

fn cubic_permutations(permutation: u8) -> u64 {
    assert!(permutation > 2);
    let mut counts: HashMap<u64, (u8, u16)> = HashMap::new();
    let mut digits = 1u64;
    while digits < 100u64.pow(3) {
        digits *= 10;
    }
    for n in 100u16.. {
        let cube = (n as u64).pow(3);
        if digits as f32 / cube as f32 <= 1f32 {
            if let Some(&n) = min(&counts, permutation) {
                return (n as u64).pow(3);
            }
            counts.clear();
            digits *= 10;
        }
        let freq = freq(cube);
        if let Some((cnt, _)) = counts.get_mut(&freq) {
            *cnt += 1;
            continue;
        }
        counts.insert(freq, (1, n));
    }
    unreachable!();
}

fn main() {
    {
        let ans = cubic_permutations(3);
        println!("{}", ans);
        assert_eq!(ans, 41063625);
    }
    {
        let ans = cubic_permutations(4);
        println!("{}", ans);
        assert_eq!(ans, 1006012008);
    }
    {
        let ans = cubic_permutations(5);
        println!("{}", ans);
        assert_eq!(ans, 127035954683);
    }
    {
        let ans = cubic_permutations(6);
        println!("{}", ans);
        assert_eq!(ans, 1000600120008);
    }
}

fn main() {
    let mut count = 0u8;
    for a in 1..=9 {
        let exp = 1f32 / (1f32 - (a as f32).log10());
        println!("a: {} \t exp: {}", a, exp);
        count += exp as u8;
    }
    println!("{}", count);
    assert_eq!(count, 49);
}

fn main() {
    let mut count = 0u8;
    for a in 1u128..=9 {
        for exp in 1.. {
            let n = a.pow(exp);
            if n < 10u128.pow(exp - 1) {
                break;
            }
            println!("{} ^ {} \t = {}", a, exp, n);
            count += 1;
        }
    }
    println!("{}", count);
    assert_eq!(count, 49);
}

• Floor and ceiling functions, Wikipedia

Real numbers

• Q.26 Reciprocal cycles

Continued fractions

• Q.57 Square root convergents

Floor function

• Q.63 Powerful digit counts

• Length of period of continued fraction for sqrt(m), m = n-th nonsquare, oeis.org
• Continued fraction expansion, Wikipedia
• https://projecteuler.net/action=quote;post_id=356667

mod fraction {
    trait MixedFraction {
        fn integer_part(&self) -> u32;
    }

    pub struct QuadraticIrrational {
        rational_part: u32,
        irrational_part: u32,
        downscaling_ratio: u32,
        pub integer_part: u32,
        pub iteration: u32,
    }

    impl MixedFraction for QuadraticIrrational {
        fn integer_part(&self) -> u32 {
            let mixed_fraction
                = self.rational_part as f64 
                + (self.irrational_part as f64).sqrt();
            (mixed_fraction / self.downscaling_ratio as f64) as u32
        }
    }

    impl QuadraticIrrational {
        pub fn new(square_free_integer: u32) -> Self {
            assert!(
                ((square_free_integer as f64).sqrt() as u32).pow(2)
                != square_free_integer
            );
            let mut q = Self {
                rational_part: 0,
                irrational_part: square_free_integer,
                downscaling_ratio: 1,
                integer_part: u32::MAX,
                iteration: 0,
            };
            q.integer_part = q.integer_part();
            q
        }
        pub fn next_iteration(&mut self) {
            self.iteration += 1;
            self.rational_part 
                = self.downscaling_ratio 
                * self.integer_part 
                - self.rational_part;
            self.downscaling_ratio
                = (self.irrational_part - self.rational_part.pow(2)) 
                / self.downscaling_ratio;
            self.integer_part = self.integer_part();
        }
    }
}

fn main() {
    let mut count = 0u32;
    for n in 2..=10000 {
        if ((n as f64).sqrt() as u32).pow(2) == n {
            continue;
        }
        let mut surd = fraction::QuadraticIrrational::new(n);
        let integer_part_orig = surd.integer_part;
        while {
            surd.next_iteration();
            surd.integer_part != integer_part_orig * 2
        } {}
        if surd.iteration % 2 != 0 {
            count += 1;
        }
    }
    println!("{}", count);
    assert_eq!(count, 1322);
}

Big numbers

• Q.56 Powerful digit sum
• Q.57 Square root convergents

mod bignum {
    #[derive(Clone)]
    pub struct BigNum {
        v: Vec<u64>,
    }

    impl BigNum {
        const TEN_MIL: u64 = 10_000_000_000;
        pub fn new(n: u8) -> Self {
            Self { v: vec![n as u64] }
        }
        fn merge(&mut self, page: usize, n: u64, carry: &mut u64) {
            if self.v.get(page).is_none() {
                self.v.push(0u64)
            }
            if let Some(con) = self.v.get_mut(page) {
                *con += n + *carry;
                if *con < Self::TEN_MIL {
                    *carry = 0;
                    return;
                }
                *carry = 1;
                *con -= Self::TEN_MIL;
            }
        }
        pub fn add(&mut self, b: &BigNum) {
            let mut p = 0usize;
            let mut carry = 0u64;
            let mut ite = b.v.iter();
            while let Some(n) = ite.next() {
                self.merge(p, *n, &mut carry);
                p += 1;
            }
            while carry != 0 {
                self.merge(p, 0, &mut carry);
                p += 1;
            }
        }
        pub fn multiply(&mut self, n: u8) {
            let mut carry = 0u64;
            for con in self.v.iter_mut() {
                *con = *con * n as u64 + carry;
                if *con < Self::TEN_MIL {
                    carry = 0;
                    continue;
                }
                carry = *con / Self::TEN_MIL;
                *con %= Self::TEN_MIL;
            }
            if carry != 0 {
                self.v.push(carry);
            }
        }
        pub fn digit_sum(&self) -> u32 {
            let mut sum = 0u32;
            for &con in &self.v {
                let mut t = con;
                while t > 0 {
                    sum += (t % 10) as u32;
                    t /= 10;
                }
            }
            sum
        }
    }
}

struct EulerNumberNumerator {
    prev: bignum::BigNum,
    value: bignum::BigNum,
    term: u8,
}

fn main() {
    let mut enn = EulerNumberNumerator {
        prev: bignum::BigNum::new(3),
        value: bignum::BigNum::new(8),
        term: 3,
    };
    while enn.term < 100 {
        enn.term += 1;
        let t = enn.value.clone();
        if enn.term % 3 == 0 {
            let k = enn.term / 3;
            enn.value.multiply(2 * k);
        }
        enn.value.add(&enn.prev);
        enn.prev = t;
    }
    let sum = enn.value.digit_sum();
    println!("{}", sum);
    assert_eq!(sum, 272);
}

Non primitive Pythagorean triples and parabolas

• Q.39 Integer right triangles

Continued fractions and their periods

• Q.64 Odd period square roots

x^2 - Dy^2 = 1 ⬄ √D ≈ x/y

• ペル方程式【連分数の魅力を伝えたい⑰】, AKITOの特異点, youtube

mod fraction {
    trait MixedFraction {
        fn integer_part(&self) -> u32;
    }

    pub struct QuadraticIrrational {
        rational_part: u32,
        irrational_part: u32,
        downscaling_ratio: u32,
        pub integer_part: u32,
        pub iteration: u32,
        integers: Vec<u32>,
    }

    impl MixedFraction for QuadraticIrrational {
        fn integer_part(&self) -> u32 {
            let mixed_fraction 
                = self.rational_part as f64 
                + (self.irrational_part as f64).sqrt();
            (mixed_fraction / self.downscaling_ratio as f64) as u32
        }
    }

    impl QuadraticIrrational {
        pub fn new(square_free_integer: u32) -> Self {
            assert!(
                ((square_free_integer as f64).sqrt() as u32).pow(2)
                != square_free_integer
            );
            let mut q = Self {
                rational_part: 0,
                irrational_part: square_free_integer,
                downscaling_ratio: 1,
                integer_part: u32::MAX,
                iteration: 0,
                integers: vec![],
            };
            q.integer_part = q.integer_part();
            q.integers.push(q.integer_part);
            q
        }
        pub fn next_iteration(&mut self) {
            self.iteration += 1;
            self.rational_part
                = self.downscaling_ratio 
                * self.integer_part 
                - self.rational_part;
            self.downscaling_ratio
                = (self.irrational_part - self.rational_part.pow(2))
                / self.downscaling_ratio;
            self.integer_part = self.integer_part();
            self.integers.push(self.integer_part);
        }
        pub fn last_numerator_approx(&self) -> f64 {
            let mut result = self.integers[0] as f64;
            let mut term_before_last = 1f64;
            for a in (&self.integers[1..self.integers.len() - 1])
                .iter()
                .map(|&a| a as f64)
            {
                let t = result.clone();
                result *= a;
                result += term_before_last;
                term_before_last = t;
            }
            result
        }
        pub fn last_denominator_approx(&self) -> f64 {
            let mut result = 1f64;
            let mut term_before_last = 0f64;
            for a in (&self.integers[1..self.integers.len() - 1])
                .iter()
                .map(|&a| a as f64)
            {
                let t = result.clone();
                result *= a;
                result += term_before_last;
                term_before_last = t;
            }
            result
        }
    }
}

fn main() {
    let mut max_numerator_aprox = 0f64;
    let mut max_d = 0u32;
    for n in 2..=1000 {
        if ((n as f64).sqrt() as u32).pow(2) == n {
            continue;
        }
        let mut surd = fraction::QuadraticIrrational::new(n);
        let integer_part_orig = surd.integer_part;
        while {
            surd.next_iteration();
            surd.integer_part != integer_part_orig * 2 || surd.iteration % 2 != 0
        } {}
        let last_numerator_approx = surd.last_numerator_approx();
        if last_numerator_approx > max_numerator_aprox {
            max_numerator_aprox = last_numerator_approx;
            max_d = n;
        }
    }

    println!("{}", max_d);
    assert_eq!(max_d, 661);
}

• Pell equation solver, Wolfram
• Mathematical dictionaries
• 世界は２乗でできている 自然にひそむ平方数の不思議

• Q.18 Maximum path sum I (identical code)

fn main() {
    let mut triangle: Vec<Vec<u16>> = data();
    triangle.push(vec![0; triangle.last().unwrap().len() + 1]);
    for y in (0..triangle.len() - 1).rev() {
        for x in 0..triangle[y].len() {
            let a = triangle[y + 1][x];
            let b = triangle[y + 1][x + 1];
            triangle[y][x] += std::cmp::max(a, b);
        }
    }
    let sum = triangle[0][0];

    println!("{}", sum);
    assert_eq!(sum, 635);
}

fn data() -> Vec<Vec<u16>> {
    vec![
        vec![59],
        vec![73,41],
        vec![52,40,09],
        vec![26,53,06,34],
        vec![10,51,87,86,81],
        vec![61,95,66,57,25,68],
        vec![90,81,80,38,92,67,73],
        vec![30,28,51,76,81,18,75,44],
        vec![84,14,95,87,62,81,17,78,58]
    ]
}

Problem 68 "Magic 5-gon ring"

Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.

Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely. For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.

It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.

Total	Solution Set
9	4,2,3; 5,3,1; 6,1,2
9	4,3,2; 6,2,1; 5,1,3
10	2,3,5; 4,5,1; 6,1,3
10	2,5,3; 6,3,1; 4,1,5
11	1,4,6; 3,6,2; 5,2,4
11	1,6,4; 5,4,2; 3,2,6
12	1,5,6; 2,6,4; 3,4,5
12	1,6,5; 3,5,4; 2,4,6

By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.

Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum 16-digit string for a "magic" 5-gon ring?

問 68 「マジックペンタゴン」

下に示す図のようなものを"magic" 3-gon ringという. これは1～6の数字を当てはめて, 各列の数字の和が9となっている. これを例として説明する.

外側のノードのうち一番小さいものの付いた列(例では4,3,2)から時計回りに回ってそれぞれ列の数字を3つ連ねて説明する. 例えば例のものは4,3,2; 6,2,1; 5,1,3という組で説明することができる.

1～6の数字を当てはめて, 各列の数字の和が等しくなるものは次の8通りある.

この組の各数字を連結して, 9桁の数字で表すことができる. 例えば, 上の図のものは4,3,2; 6,2,1; 5,1,3であるので432621513である.

さて, 下の図に1～10の数字を当てはめ, 各列の数字の和が等しくなる"magic" 5-gon ringを作って, それを表す16桁または17桁の数字のうち, 16桁のものの最大の数字を答えよ.

Generation of permurations using recursion

• Q.31 Coin sums
• Q.41 Pandigital prime
• Q.43 Sub-string divisibility
• Q.60 Prime pair sets

#[derive(Clone)]
struct MagicGonRing {
    mat: [Vec<u8>; 3],
    width: usize,
}

impl MagicGonRing {
    fn new(ngon: u8) -> Self {
        let n = ngon as usize;
        Self {
            mat: [vec![0u8; n], vec![0u8; n], vec![0u8; n]],
            width: n,
        }
    }
    fn fill(&mut self, initial: u8) -> Vec<MagicGonRing> {
        assert!(initial > 0 && initial <= self.width as u8 * 2);
        self.mat[0][0] = initial;
        let used = 1u32 << initial;
        let mut perfect_rings: Vec<MagicGonRing> = vec![];
        self.dig(used, 0, 1, &mut perfect_rings);
        perfect_rings
    }
    fn is_rotational_variation(&self, y: usize, n: u8) -> bool {
        y == 0 && n < self.mat[0][0]
    }
    fn is_violation_of_homogeneity(&mut self, x: usize, y: usize, n: u8) -> bool {
        if y == 0 || x == 0 {
            return false;
        }
        let total = self.mat[0][x - 1] + self.mat[1][x - 1] + n;
        if x == 1 {
            self.mat[2][x] = total;
            return false;
        }
        if self.mat[2][x - 1] != total {
            return true;
        }
        if x == self.width - 1 {
            let conjunction = self.mat[0][x] + n + self.mat[1][0];
            if conjunction != total {
                return true;
            }
            self.mat[2][0] = conjunction;
        }
        self.mat[2][x] = total;
        false
    }
    fn dig(&mut self, used: u32, x: usize, y: usize, drain: &mut Vec<MagicGonRing>) {
        if x > self.width - 1 {
            drain.push(self.clone());
            return;
        }
        let numbers = 1..=2 * self.width as u8;
        for n in numbers.filter(|&n| 1 << n & used == 0) {
            if self.is_rotational_variation(y, n) {
                continue;
            }
            if self.is_violation_of_homogeneity(x, y, n) {
                continue;
            }
            self.mat[y][x] = n;
            self.dig(used | 1u32 << n, x + y, y ^ 1, drain);
        }
    }
    fn stringfy(&self) -> String {
        let mut s = String::new();
        for i in 0..self.width {
            s.push_str(self.mat[0][i].to_string().as_str());
            s.push_str(self.mat[1][i].to_string().as_str());
            let conjunction = if i != self.width - 1 { i + 1 } else { 0 };
            s.push_str(self.mat[1][conjunction].to_string().as_str());
        }
        s
    }
}

fn main() {
    {
        let mut ring = MagicGonRing::new(3);
        for initial in (1u8..=6).rev() {
            let perfect_rings = ring.fill(initial);
            perfect_rings.iter().for_each(|g| println!("{:?}", g.mat));
        }
    }
    {
        let mut ans = None;
        let mut ring = MagicGonRing::new(3);
        for initial in (1u8..=4).rev() {
            let perfect_rings = ring.fill(initial);
            let mut list = perfect_rings
                .iter()
                .map(|g| g.stringfy())
                .collect::<Vec<String>>();
            list.sort();
            if let Some(s) = list.pop() {
                ans.insert(s);
                break;
            }
        }
        let ans = ans.expect("answer must exist");
        println!("{}", ans);
        assert_eq!(ans, "432621513");
    }
    {
        let mut ans = None;
        let mut ring = MagicGonRing::new(5);
        for initial in (1u8..=6).rev() {
            let perfect_rings = ring.fill(initial);
            let mut list = perfect_rings
                .iter()
                .map(|g| g.stringfy())
                .filter(|s| s.len() == 16)
                .collect::<Vec<String>>();
            list.sort();
            if let Some(s) = list.pop() {
                ans.insert(s);
                break;
            }
        }
        let ans = ans.expect("answer must exist");
        println!("{}", ans);
        assert_eq!(ans, "6531031914842725");
    }
}

• Q.31 Coin sums

Since the dataset of the question is too large, it's using a mini set.

fn main() {
    let mut table = vec![
        vec![131, 673, 234, 103, 18],
        vec![201, 96, 342, 965, 150],
        vec![630, 803, 746, 422, 111],
        vec![537, 699, 497, 121, 956],
        vec![805, 732, 524, 37, 331]
    ];
    for y in 0..table.len() {
        for x in 0..table[0].len() {
            table[y][x] += match (y, x) {
                (0, 0) => continue,
                (0, _) => table[y][x - 1],
                (_, 0) => table[y - 1][x],
                _ => std::cmp::min(table[y][x - 1], table[y - 1][x]),
            }
        }
    }
    let min = table[table.len() - 1][table[table.len() - 1].len() - 1];

    println!("{}", min);
    assert_eq!(min, 2427);
}

• Q.31 Coin sums
• Q.81 Path sum: two ways

Since the dataset of the question is too large, it's using a mini set.

fn row_internal_loop(
    col: usize,
    row: usize,
    table: &[[u32; 5]; 5],
    determineds: &Vec<u32>,
) -> u32 {
    let mut min = u32::MAX;
    {
        let mut d = 0u32;
        for r in (0..row).rev() {
            d += table[r][col];
            min = std::cmp::min(min, determineds[r] + d);
        }
    }
    min = std::cmp::min(min, determineds[row]);
    {
        let mut d = 0u32;
        for r in row + 1..table.len() {
            d += table[r][col];
            min = std::cmp::min(min, determineds[r] + d);
        }
    }
    min
}

fn main() {
    let table: [[u32; 5]; 5] = [
        [131, 673, 234, 103, 18],
        [201, 96, 342, 965, 150],
        [630, 803, 746, 422, 111],
        [537, 699, 497, 121, 956],
        [805, 732, 524, 37, 331]
    ];
    let mut determineds = vec![0u32; table.len()];
    let mut estimations = vec![0u32; table.len()];
    for col in 0..table[0].len() {
        for row in 0..table.len() {
            let min = row_internal_loop(col, row, &table, &determineds);
            estimations[row] = table[row][col] + min;
        }
        determineds.clone_from(&estimations);
    }
    let min = estimations
        .iter()
        .min()
        .map(|&m| m)
        .expect("the input table must have at least one row");

    println!("{}", min);
    assert_eq!(min, 994);
}

• Q.31 Coin sums
• Q.81 Path sum: two ways
• Q.82 Path sum: three ways

Since the dataset of the question is too large, it's using a mini set.

• Q.22 Names scores - Heap sort
• Module std::collections::binary_heap

use std::{cmp::Ordering, collections::BinaryHeap};

#[derive(Copy, Clone, Eq, PartialEq)]
struct Vertex {
    cost: u32,
    xy: (usize, usize),
}

impl Ord for Vertex {
    fn cmp(&self, other: &Self) -> Ordering {
        other.cost.cmp(&self.cost)
    }
}

impl PartialOrd for Vertex {
    fn partial_cmp(&self, other: &Self) -> Option<Ordering> {
        Some(self.cmp(other))
    }
}

fn update_adjacents(
    v: Vertex,
    table: &[[u32; 5]; 5],
    visited: &Vec<Vec<bool>>,
    estimations: &mut Vec<Vec<u32>>,
    pq: &mut BinaryHeap<Vertex>,
) {
    let Vertex { xy: (x, y), cost } = v;
    if y > 0 {
        let t = y - 1;
        if !visited[t][x] {
            let e = &mut estimations[t][x];
            *e = std::cmp::min(*e, table[t][x] + cost);
            pq.push(Vertex {
                cost: *e,
                xy: (x, t),
            });
        }
    }
    if x < table[0].len() - 1 {
        let t = x + 1;
        if !visited[y][t] {
            let e = &mut estimations[y][t];
            *e = std::cmp::min(*e, table[y][t] + cost);
            pq.push(Vertex {
                cost: *e,
                xy: (t, y),
            });
        }
    }
    if y < table.len() - 1 {
        let t = y + 1;
        if !visited[t][x] {
            let e = &mut estimations[t][x];
            *e = std::cmp::min(*e, table[t][x] + cost);
            pq.push(Vertex {
                cost: *e,
                xy: (x, t),
            });
        }
    }
    if x > 0 {
        let t = x - 1;
        if !visited[y][t] {
            let e = &mut estimations[y][t];
            *e = std::cmp::min(*e, table[y][t] + cost);
            pq.push(Vertex {
                cost: *e,
                xy: (t, y),
            });
        }
    }
}

fn suggest_next_vertex(pq: &mut BinaryHeap<Vertex>, visited: &Vec<Vec<bool>>) -> Option<Vertex> {
    loop {
        match pq.pop() {
            None => return None,
            Some(v) if !visited[v.xy.1][v.xy.0] => return Some(v),
            _ => (),
        }
    }
}

fn main() {
    let table: [[u32; 5]; 5] = [
        [131, 673, 234, 103, 18],
        [201, 96, 342, 965, 150],
        [630, 803, 746, 422, 111],
        [537, 699, 497, 121, 956],
        [805, 732, 524, 37, 331]
    ];
    let (w, h) = (table[0].len(), table.len());
    let mut visited = vec![vec![false; w]; h];
    let mut estimations = vec![vec![u32::MAX; w]; h];

    estimations[0][0] = table[0][0];
    let mut pq = std::collections::BinaryHeap::<Vertex>::new();
    pq.push(Vertex {
        cost: estimations[0][0],
        xy: (0, 0),
    });
    let is_goal = |x, y| -> bool { x == w - 1 && y == h - 1 };
    let min = loop {
        let vertex = suggest_next_vertex(&mut pq, &visited)
            .expect("Goal was unreachable!");
        let (x, y) = vertex.xy;
        if is_goal(x, y) {
            break vertex.cost;
        }
        visited[y][x] = true;
        update_adjacents(vertex, &table, &visited, &mut estimations, &mut pq);
    };

    println!("{}", min);
    assert_eq!(min, 2297);
}

TODO: implement a primarity queue by myself

fn update_adjacents(
    x: usize,
    y: usize,
    table: &[[u32; 5]; 5],
    visited: &Vec<Vec<bool>>,
    estimations: &mut Vec<Vec<u32>>,
) {
    let cost = estimations[y][x];
    if y > 0 {
        let t = y - 1;
        if !visited[t][x] {
            let e = &mut estimations[t][x];
            *e = std::cmp::min(*e, table[t][x] + cost);
        }
    }
    if x < table[0].len() - 1 {
        let t = x + 1;
        if !visited[y][t] {
            let e = &mut estimations[y][t];
            *e = std::cmp::min(*e, table[y][t] + cost);
        }
    }
    if y < table.len() - 1 {
        let t = y + 1;
        if !visited[t][x] {
            let e = &mut estimations[t][x];
            *e = std::cmp::min(*e, table[t][x] + cost);
        }
    }
    if x > 0 {
        let t = x - 1;
        if !visited[y][t] {
            let e = &mut estimations[y][t];
            *e = std::cmp::min(*e, table[y][t] + cost);
        }
    }
}

fn suggest_next_vertex(
    table: &[[u32; 5]; 5],
    visited: &Vec<Vec<bool>>,
    estimations: &Vec<Vec<u32>>,
) -> Option<(usize, usize)> {
    let mut next: Option<(usize, usize)> = None;
    let mut minimum_estimation = u32::MAX;
    for y in 0..table.len() {
        for x in 0..table[0].len() {
            if visited[y][x] {
                continue;
            }
            if estimations[y][x] < minimum_estimation {
                minimum_estimation = estimations[y][x];
                next = Some((x, y));
            }
        }
    }
    next
}

fn main() {
    let table: [[u32; 5]; 5] = [
        [131, 673, 234, 103, 18],
        [201, 96, 342, 965, 150],
        [630, 803, 746, 422, 111],
        [537, 699, 497, 121, 956],
        [805, 732, 524, 37, 331]
    ];
    let (w, h) = (table[0].len(), table.len());
    let mut visited = vec![vec![false; w]; h];
    let mut estimations = vec![vec![u32::MAX; w]; h];

    estimations[0][0] = table[0][0];
    let is_goal = |x, y| -> bool { x == w - 1 && y == h - 1 };
    let min = loop {
        let (x, y) = suggest_next_vertex(&table, &visited, &estimations)
            .expect("Goal was unreachable!");
        if is_goal(x, y) {
            break estimations[y][x];
        }
        visited[y][x] = true;
        update_adjacents(x, y, &table, &visited, &mut estimations);
    };

    println!("{}", min);
    assert_eq!(min, 2297);
}

<style type="text/css">

/----------------------------------------------------------------------------- | Copyright (c) Jupyter Development Team. | Distributed under the terms of the Modified BSD License. |----------------------------------------------------------------------------/

/* The following CSS variables define the main, public API for styling JupyterLab. These variables should be used by all plugins wherever possible. In other words, plugins should not define custom colors, sizes, etc unless absolutely necessary. This enables users to change the visual theme of JupyterLab by changing these variables.

Many variables appear in an ordered sequence (0,1,2,3). These sequences are designed to work well together, so for example, --jp-border-color1 should be used with --jp-layout-color1. The numbers have the following meanings:

• 0: super-primary, reserved for special emphasis
• 1: primary, most important under normal situations
• 2: secondary, next most important under normal situations
• 3: tertiary, next most important under normal situations

Throughout JupyterLab, we are mostly following principles from Google's Material Design when selecting colors. We are not, however, following all of MD as it is not optimized for dense, information rich UIs. */

:root { /* Elevation

• We style box-shadows using Material Design's idea of elevation. These particular numbers are taken from here:
• https://github.com/material-components/material-components-web
• https://material-components-web.appspot.com/elevation.html */

--jp-shadow-base-lightness: 0; --jp-shadow-umbra-color: rgba( var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), 0.2 ); --jp-shadow-penumbra-color: rgba( var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), 0.14 ); --jp-shadow-ambient-color: rgba( var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), var(--jp-shadow-base-lightness), 0.12 ); --jp-elevation-z0: none; --jp-elevation-z1: 0px 2px 1px -1px var(--jp-shadow-umbra-color), 0px 1px 1px 0px var(--jp-shadow-penumbra-color), 0px 1px 3px 0px var(--jp-shadow-ambient-color); --jp-elevation-z2: 0px 3px 1px -2px var(--jp-shadow-umbra-color), 0px 2px 2px 0px var(--jp-shadow-penumbra-color), 0px 1px 5px 0px var(--jp-shadow-ambient-color); --jp-elevation-z4: 0px 2px 4px -1px var(--jp-shadow-umbra-color), 0px 4px 5px 0px var(--jp-shadow-penumbra-color), 0px 1px 10px 0px var(--jp-shadow-ambient-color); --jp-elevation-z6: 0px 3px 5px -1px var(--jp-shadow-umbra-color), 0px 6px 10px 0px var(--jp-shadow-penumbra-color), 0px 1px 18px 0px var(--jp-shadow-ambient-color); --jp-elevation-z8: 0px 5px 5px -3px var(--jp-shadow-umbra-color), 0px 8px 10px 1px var(--jp-shadow-penumbra-color), 0px 3px 14px 2px var(--jp-shadow-ambient-color); --jp-elevation-z12: 0px 7px 8px -4px var(--jp-shadow-umbra-color), 0px 12px 17px 2px var(--jp-shadow-penumbra-color), 0px 5px 22px 4px var(--jp-shadow-ambient-color); --jp-elevation-z16: 0px 8px 10px -5px var(--jp-shadow-umbra-color), 0px 16px 24px 2px var(--jp-shadow-penumbra-color), 0px 6px 30px 5px var(--jp-shadow-ambient-color); --jp-elevation-z20: 0px 10px 13px -6px var(--jp-shadow-umbra-color), 0px 20px 31px 3px var(--jp-shadow-penumbra-color), 0px 8px 38px 7px var(--jp-shadow-ambient-color); --jp-elevation-z24: 0px 11px 15px -7px var(--jp-shadow-umbra-color), 0px 24px 38px 3px var(--jp-shadow-penumbra-color), 0px 9px 46px 8px var(--jp-shadow-ambient-color);

/* Borders

• The following variables, specify the visual styling of borders in JupyterLab. */

--jp-border-width: 1px; --jp-border-color0: var(--md-grey-400); --jp-border-color1: var(--md-grey-400); --jp-border-color2: var(--md-grey-300); --jp-border-color3: var(--md-grey-200); --jp-border-radius: 2px;

/* UI Fonts

• The UI font CSS variables are used for the typography all of the JupyterLab
• user interface elements that are not directly user generated content.
• The font sizing here is done assuming that the body font size of --jp-ui-font-size1
• is applied to a parent element. When children elements, such as headings, are sized
• in em all things will be computed relative to that body size. */

--jp-ui-font-scale-factor: 1.2; --jp-ui-font-size0: 0.83333em; --jp-ui-font-size1: 13px; /* Base font size */ --jp-ui-font-size2: 1.2em; --jp-ui-font-size3: 1.44em;

--jp-ui-font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', Helvetica, Arial, sans-serif, 'Apple Color Emoji', 'Segoe UI Emoji', 'Segoe UI Symbol';

/*

• Use these font colors against the corresponding main layout colors.
• In a light theme, these go from dark to light. */

/* Defaults use Material Design specification */ --jp-ui-font-color0: rgba(0, 0, 0, 1); --jp-ui-font-color1: rgba(0, 0, 0, 0.87); --jp-ui-font-color2: rgba(0, 0, 0, 0.54); --jp-ui-font-color3: rgba(0, 0, 0, 0.38);

/*

• Use these against the brand/accent/warn/error colors.
• These will typically go from light to darker, in both a dark and light theme. */

--jp-ui-inverse-font-color0: rgba(255, 255, 255, 1); --jp-ui-inverse-font-color1: rgba(255, 255, 255, 1); --jp-ui-inverse-font-color2: rgba(255, 255, 255, 0.7); --jp-ui-inverse-font-color3: rgba(255, 255, 255, 0.5);

/* Content Fonts

• Content font variables are used for typography of user generated content.
• The font sizing here is done assuming that the body font size of --jp-content-font-size1
• is applied to a parent element. When children elements, such as headings, are sized
• in em all things will be computed relative to that body size. */

--jp-content-line-height: 1.6; --jp-content-font-scale-factor: 1.2; --jp-content-font-size0: 0.83333em; --jp-content-font-size1: 14px; /* Base font size */ --jp-content-font-size2: 1.2em; --jp-content-font-size3: 1.44em; --jp-content-font-size4: 1.728em; --jp-content-font-size5: 2.0736em;

/* This gives a magnification of about 125% in presentation mode over normal. */ --jp-content-presentation-font-size1: 17px;

--jp-content-heading-line-height: 1; --jp-content-heading-margin-top: 1.2em; --jp-content-heading-margin-bottom: 0.8em; --jp-content-heading-font-weight: 500;

/* Defaults use Material Design specification */ --jp-content-font-color0: rgba(0, 0, 0, 1); --jp-content-font-color1: rgba(0, 0, 0, 0.87); --jp-content-font-color2: rgba(0, 0, 0, 0.54); --jp-content-font-color3: rgba(0, 0, 0, 0.38);

--jp-content-link-color: var(--md-blue-700);

--jp-content-font-family: -apple-system, BlinkMacSystemFont, 'Segoe UI', Helvetica, Arial, sans-serif, 'Apple Color Emoji', 'Segoe UI Emoji', 'Segoe UI Symbol';

/*

• Code Fonts
• Code font variables are used for typography of code and other monospaces content. */

--jp-code-font-size: 13px; --jp-code-line-height: 1.3077; /* 17px for 13px base / --jp-code-padding: 5px; / 5px for 13px base, codemirror highlighting needs integer px value */ --jp-code-font-family-default: Menlo, Consolas, 'DejaVu Sans Mono', monospace; --jp-code-font-family: var(--jp-code-font-family-default);

/* This gives a magnification of about 125% in presentation mode over normal. */ --jp-code-presentation-font-size: 16px;

/* may need to tweak cursor width if you change font size */ --jp-code-cursor-width0: 1.4px; --jp-code-cursor-width1: 2px; --jp-code-cursor-width2: 4px;

/* Layout

• The following are the main layout colors use in JupyterLab. In a light
• theme these would go from light to dark. */

--jp-layout-color0: white; --jp-layout-color1: white; --jp-layout-color2: var(--md-grey-200); --jp-layout-color3: var(--md-grey-400); --jp-layout-color4: var(--md-grey-600);

/* Inverse Layout

• The following are the inverse layout colors use in JupyterLab. In a light
• theme these would go from dark to light. */

--jp-inverse-layout-color0: #111111; --jp-inverse-layout-color1: var(--md-grey-900); --jp-inverse-layout-color2: var(--md-grey-800); --jp-inverse-layout-color3: var(--md-grey-700); --jp-inverse-layout-color4: var(--md-grey-600);

/* Brand/accent */

--jp-brand-color0: var(--md-blue-900); --jp-brand-color1: var(--md-blue-700); --jp-brand-color2: var(--md-blue-300); --jp-brand-color3: var(--md-blue-100); --jp-brand-color4: var(--md-blue-50);

--jp-accent-color0: var(--md-green-900); --jp-accent-color1: var(--md-green-700); --jp-accent-color2: var(--md-green-300); --jp-accent-color3: var(--md-green-100);

/* State colors (warn, error, success, info) */

--jp-warn-color0: var(--md-orange-900); --jp-warn-color1: var(--md-orange-700); --jp-warn-color2: var(--md-orange-300); --jp-warn-color3: var(--md-orange-100);

--jp-error-color0: var(--md-red-900); --jp-error-color1: var(--md-red-700); --jp-error-color2: var(--md-red-300); --jp-error-color3: var(--md-red-100);

--jp-success-color0: var(--md-green-900); --jp-success-color1: var(--md-green-700); --jp-success-color2: var(--md-green-300); --jp-success-color3: var(--md-green-100);

--jp-info-color0: var(--md-cyan-900); --jp-info-color1: var(--md-cyan-700); --jp-info-color2: var(--md-cyan-300); --jp-info-color3: var(--md-cyan-100);

/* Cell specific styles */

--jp-cell-padding: 5px;

--jp-cell-collapser-width: 8px; --jp-cell-collapser-min-height: 20px; --jp-cell-collapser-not-active-hover-opacity: 0.6;

--jp-cell-editor-background: var(--md-grey-100); --jp-cell-editor-border-color: var(--md-grey-300); --jp-cell-editor-box-shadow: inset 0 0 2px var(--md-blue-300); --jp-cell-editor-active-background: var(--jp-layout-color0); --jp-cell-editor-active-border-color: var(--jp-brand-color1);

--jp-cell-prompt-width: 64px; --jp-cell-prompt-font-family: var(--jp-code-font-family-default); --jp-cell-prompt-letter-spacing: 0px; --jp-cell-prompt-opacity: 1; --jp-cell-prompt-not-active-opacity: 0.5; --jp-cell-prompt-not-active-font-color: var(--md-grey-700); /* A custom blend of MD grey and blue 600

• See https://meyerweb.com/eric/tools/color-blend/#546E7A:1E88E5:5:hex / --jp-cell-inprompt-font-color: #307fc1; / A custom blend of MD grey and orange 600
• https://meyerweb.com/eric/tools/color-blend/#546E7A:F4511E:5:hex */ --jp-cell-outprompt-font-color: #bf5b3d;

/* Notebook specific styles */

--jp-notebook-padding: 10px; --jp-notebook-select-background: var(--jp-layout-color1); --jp-notebook-multiselected-color: var(--md-blue-50);

/* The scroll padding is calculated to fill enough space at the bottom of the notebook to show one single-line cell (with appropriate padding) at the top when the notebook is scrolled all the way to the bottom. We also subtract one pixel so that no scrollbar appears if we have just one single-line cell in the notebook. This padding is to enable a 'scroll past end' feature in a notebook. */ --jp-notebook-scroll-padding: calc( 100% - var(--jp-code-font-size) * var(--jp-code-line-height) - var(--jp-code-padding) - var(--jp-cell-padding) - 1px );

/* Rendermime styles */

--jp-rendermime-error-background: #fdd; --jp-rendermime-table-row-background: var(--md-grey-100); --jp-rendermime-table-row-hover-background: var(--md-light-blue-50);

/* Dialog specific styles */

--jp-dialog-background: rgba(0, 0, 0, 0.25);

/* Console specific styles */

--jp-console-padding: 10px;

/* Toolbar specific styles */

--jp-toolbar-border-color: var(--jp-border-color1); --jp-toolbar-micro-height: 8px; --jp-toolbar-background: var(--jp-layout-color1); --jp-toolbar-box-shadow: 0px 0px 2px 0px rgba(0, 0, 0, 0.24); --jp-toolbar-header-margin: 4px 4px 0px 4px; --jp-toolbar-active-background: var(--md-grey-300);

/* Statusbar specific styles */

--jp-statusbar-height: 24px;

/* Input field styles */

--jp-input-box-shadow: inset 0 0 2px var(--md-blue-300); --jp-input-active-background: var(--jp-layout-color1); --jp-input-hover-background: var(--jp-layout-color1); --jp-input-background: var(--md-grey-100); --jp-input-border-color: var(--jp-border-color1); --jp-input-active-border-color: var(--jp-brand-color1); --jp-input-active-box-shadow-color: rgba(19, 124, 189, 0.3);

/* General editor styles */

--jp-editor-selected-background: #d9d9d9; --jp-editor-selected-focused-background: #d7d4f0; --jp-editor-cursor-color: var(--jp-ui-font-color0);

/* Code mirror specific styles */

--jp-mirror-editor-keyword-color: #008000; --jp-mirror-editor-atom-color: #88f; --jp-mirror-editor-number-color: #080; --jp-mirror-editor-def-color: #00f; --jp-mirror-editor-variable-color: var(--md-grey-900); --jp-mirror-editor-variable-2-color: #05a; --jp-mirror-editor-variable-3-color: #085; --jp-mirror-editor-punctuation-color: #05a; --jp-mirror-editor-property-color: #05a; --jp-mirror-editor-operator-color: #aa22ff; --jp-mirror-editor-comment-color: #408080; --jp-mirror-editor-string-color: #ba2121; --jp-mirror-editor-string-2-color: #708; --jp-mirror-editor-meta-color: #aa22ff; --jp-mirror-editor-qualifier-color: #555; --jp-mirror-editor-builtin-color: #008000; --jp-mirror-editor-bracket-color: #997; --jp-mirror-editor-tag-color: #170; --jp-mirror-editor-attribute-color: #00c; --jp-mirror-editor-header-color: blue; --jp-mirror-editor-quote-color: #090; --jp-mirror-editor-link-color: #00c; --jp-mirror-editor-error-color: #f00; --jp-mirror-editor-hr-color: #999;

/* Vega extension styles */

--jp-vega-background: white;

/* Sidebar-related styles */

--jp-sidebar-min-width: 250px;

/* Search-related styles */

--jp-search-toggle-off-opacity: 0.5; --jp-search-toggle-hover-opacity: 0.8; --jp-search-toggle-on-opacity: 1; --jp-search-selected-match-background-color: rgb(245, 200, 0); --jp-search-selected-match-color: black; --jp-search-unselected-match-background-color: var( --jp-inverse-layout-color0 ); --jp-search-unselected-match-color: var(--jp-ui-inverse-font-color0);

/* Icon colors that work well with light or dark backgrounds */ --jp-icon-contrast-color0: var(--md-purple-600); --jp-icon-contrast-color1: var(--md-green-600); --jp-icon-contrast-color2: var(--md-pink-600); --jp-icon-contrast-color3: var(--md-blue-600); }

<script src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.7/latest.js?config=TeX-AMS_CHTML-full,Safe"> </script>
<!-- MathJax configuration -->
<script type="text/x-mathjax-config">
init_mathjax = function() {
    if (window.MathJax) {
    // MathJax loaded
        MathJax.Hub.Config({
            TeX: {
                equationNumbers: {
                autoNumber: "AMS",
                useLabelIds: true
                }
            },
            tex2jax: {
                inlineMath: [ ['$','$'], ["\\(","\\)"] ],
                displayMath: [ ['$$','$$'], ["\\[","\\]"] ],
                processEscapes: true,
                processEnvironments: true
            },
            displayAlign: 'center',
            CommonHTML: {
                linebreaks: { 
                automatic: true 
                }
            }
        });
    
        MathJax.Hub.Queue(["Typeset", MathJax.Hub]);
    }
}
init_mathjax();
</script>
<!-- End of mathjax configuration --></head>

In [1]:

ls

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Go.ipynb        Untitled1.ipynb            java.ipynb    rust.ipynb
Untitled.ipynb  java-ryoji-20211025.ipynb  python.ipynb  typescript.ipynb

In [3]:

echo "abc" | tee abc.txt && stat abc.txt

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

abc
  File: abc.txt
  Size: 4         	Blocks: 24         IO Block: 4096   regular file
Device: 38h/56d	Inode: 10003282    Links: 1
Access: (0664/-rw-rw-r--)  Uid: ( 1000/   ryoji)   Gid: ( 1000/   ryoji)
Access: 2021-10-25 21:40:37.145779673 +0900
Modify: 2021-10-25 21:42:38.355751530 +0900
Change: 2021-10-25 21:42:38.355751530 +0900
 Birth: -

In [4]:

cat abc.txt | sed 's/b/d/g'

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

adc

In [42]:

tr abc XYZ < abc.txt #translate

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

XYZ

In [7]:

whoami

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

ryoji

In [11]:

uname --all

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Linux ubuntu 5.4.0-84-generic #94-Ubuntu SMP Thu Aug 26 20:27:37 UTC 2021 x86_64 x86_64 x86_64 GNU/Linux

In [21]:

echo "first-name last-name" | awk '{print $2}'

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

last-name

In [36]:

find . -maxdepth 1 -name 'j*.ipynb' -type f | xargs jq '.metadata.kernelspec'

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

{
  "display_name": "Java",
  "language": "java",
  "name": "java"
}
{
  "display_name": "Java",
  "language": "java",
  "name": "java"
}

In [33]:

du #disk usage

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

300	./.ipynb_checkpoints
632	.

In [34]:

df / #disk file system

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Filesystem     1K-blocks      Used Available Use% Mounted on
/dev/sda5      229484764 184497236  33307336  85% /

In [35]:

wc --chars abc.txt #word count

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

4 abc.txt

In [7]:

sha1sum abc.txt

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

03cfd743661f07975fa2f1220c5194cbaff48451  abc.txt

In [8]:

date

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Mon Oct 25 22:09:41 JST 2021

In [10]:

uuidgen

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

c61fff27-3fbb-4da1-8598-0f20282aaafc

In [16]:

openssl rand -hex 1 #random 0 up to 255

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

8c

In [32]:

echo "8c" | tr [:lower:] [:upper:] | xargs echo "obase=10; ibase=16; " | bc

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

140

In [5]:

cat << EOF > a.yaml
items:
    - part_no:   A4786
      descrip:   Water Bucket (Filled)
      price:     1.47
      quantity:  4
EOF

 </div>

In [39]:

yq e '.items[0]' a.yaml

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

part_no: A4786
descrip: Water Bucket (Filled)
price: 1.47
quantity: 4

In [40]:

curl --head https://google.com

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

HTTP/2 301 
location: https://www.google.com/
content-type: text/html; charset=UTF-8
date: Mon, 25 Oct 2021 13:33:55 GMT
expires: Wed, 24 Nov 2021 13:33:55 GMT
cache-control: public, max-age=2592000
server: gws
content-length: 220
x-xss-protection: 0
x-frame-options: SAMEORIGIN
alt-svc: h3=":443"; ma=2592000,h3-29=":443"; ma=2592000,h3-Q050=":443"; ma=2592000,h3-Q046=":443"; ma=2592000,h3-Q043=":443"; ma=2592000

In [41]:

factor 360

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

360: 2 2 2 3 3 5

In [43]:

date

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Mon Oct 25 22:38:04 JST 2021

In [44]:

if [ -s abc.txt ]
then
    echo "abc isn't an empty file"
else
    echo "abc is an empty file"
fi

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

abc isn't an empty file

In [53]:

for i in $(seq 0 5)
do
    echo "$i"
done

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

0
1
2
3
4
5

In [52]:

for ((i=0; i < 4; i++))
do
    echo $i
done

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

0
1
2
3

In [69]:

# ##*/ extracts the filename from a full path
n=$(ls *.yaml)\
&& echo "${n##*/}"\
&& n=$(basename "${n##*/}" .yaml)\
&& echo $n

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

a.yaml
a

In [77]:

foo="1,2 3 4"
txt=(${foo//,/ })
IFS=' ' read -r -a arr <<< "$txt"
for ((i = 0; i < ${#arr[@]}; i++))
do
  echo "${arr[$i]}"
done
for e in "${arr[@]}"
do
  echo "$e"
done

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

1
2
3
4
1
2
3
4

for

$ ls *.zip | parallel unzip {}
$ find . -type f -name "*.zip" -exec unzip '{}' \;

In [1]:

cd /home/ryoji/image-slicer/
IFS=$'\n'
files=$(ls -1 high_school_math_slices/ | grep jpg | sort)
for e in $files
do
  parent=$(echo $e | sed -e 's/\([0-9]\)_.*/\1/')'.jpg'
  echo -e "<img src=\"$e\">\t<img src=\"$parent\">" >> high-school-math.tab
done

 </div>

In [1]:

cat a.tar.gz | xxd | head

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

00000000: 612e 7961 6d6c 0000 0000 0000 0000 0000  a.yaml..........
00000010: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000020: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000030: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000040: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000050: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000060: 0000 0000 3030 3030 3636 3400 3030 3031  ....0000664.0001
00000070: 3735 3000 3030 3031 3735 3000 3030 3030  750.0001750.0000
00000080: 3030 3030 3135 3600 3134 3133 3535 3432  0000156.14135542
00000090: 3030 3300 3031 3132 3335 0020 3000 0000  003.011235. 0...
xxd: Broken pipe

In [90]:

echo -n "iVBORw0KGgoAAAANSUhEUgAAABAAAAAPBAMAAAAfXVIcAAAAD1BMVEV63/39//w5TVIZFhXDjXbHNiz1AAAARUlEQVR4nJTJUQ3AIAwG4aMzsBYD9FdQEfjXtJBiYPf0JYeHJKUTC8CShYNjaMwas4xoJNHrgKdo7H0x3ovTP3wBAAD//9u1Bcrd6KY0AAAAAElFTkSuQmCC"\
| base64 -d | base64

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

iVBORw0KGgoAAAANSUhEUgAAABAAAAAPBAMAAAAfXVIcAAAAD1BMVEV63/39//w5TVIZFhXDjXbH
Niz1AAAARUlEQVR4nJTJUQ3AIAwG4aMzsBYD9FdQEfjXtJBiYPf0JYeHJKUTC8CShYNjaMwas4xo
JNHrgKdo7H0x3ovTP3wBAAD//9u1Bcrd6KY0AAAAAElFTkSuQmCC

In [ ]:

cat ./a.yaml |
awk '{print $2}' |
while read -r first
do
  echo "${first}" |
  tr 012345678 999999999
done

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

part_no:
Water
9.99
9

In [3]:

ssh-keygen --help

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

unknown option -- -
usage: ssh-keygen [-q] [-b bits] [-C comment] [-f output_keyfile] [-m format]
                  [-t dsa | ecdsa | ecdsa-sk | ed25519 | ed25519-sk | rsa]
                  [-N new_passphrase] [-O option] [-w provider]
       ssh-keygen -p [-f keyfile] [-m format] [-N new_passphrase]
                   [-P old_passphrase]
       ssh-keygen -i [-f input_keyfile] [-m key_format]
       ssh-keygen -e [-f input_keyfile] [-m key_format]
       ssh-keygen -y [-f input_keyfile]
       ssh-keygen -c [-C comment] [-f keyfile] [-P passphrase]
       ssh-keygen -l [-v] [-E fingerprint_hash] [-f input_keyfile]
       ssh-keygen -B [-f input_keyfile]
       ssh-keygen -D pkcs11
       ssh-keygen -F hostname [-lv] [-f known_hosts_file]
       ssh-keygen -H [-f known_hosts_file]
       ssh-keygen -K [-w provider]
       ssh-keygen -R hostname [-f known_hosts_file]
       ssh-keygen -r hostname [-g] [-f input_keyfile]
       ssh-keygen -M generate [-O option] output_file
       ssh-keygen -M screen [-f input_file] [-O option] output_file
       ssh-keygen -I certificate_identity -s ca_key [-hU] [-D pkcs11_provider]
                  [-n principals] [-O option] [-V validity_interval]
                  [-z serial_number] file ...
       ssh-keygen -L [-f input_keyfile]
       ssh-keygen -A [-f prefix_path]
       ssh-keygen -k -f krl_file [-u] [-s ca_public] [-z version_number]
                  file ...
       ssh-keygen -Q -f krl_file file ...
       ssh-keygen -Y find-principals -s signature_file -f allowed_signers_file
       ssh-keygen -Y check-novalidate -n namespace -s signature_file
       ssh-keygen -Y sign -f key_file -n namespace file ...
       ssh-keygen -Y verify -f allowed_signers_file -I signer_identity
       		-n namespace -s signature_file [-r revocation_file]

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

In [8]:

tar -cvf a.tar.gz a.yaml && tar -xvf a.tar.gz -C . #tar+gunzip

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

a.yaml
a.yaml

In [10]:

ssh -p 4118 ryoji@localhost

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

ssh: connect to host localhost port 4118: Connection refused

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

In [11]:

netstat -tulpn

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

(Not all processes could be identified, non-owned process info
 will not be shown, you would have to be root to see it all.)
Active Internet connections (only servers)
Proto Recv-Q Send-Q Local Address           Foreign Address         State       PID/Program name    
tcp        0      0 127.0.0.1:53            0.0.0.0:*               LISTEN      -                   
tcp        0      0 0.0.0.0:46485           0.0.0.0:*               LISTEN      -                   
tcp        0      0 0.0.0.0:22              0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:50999         0.0.0.0:*               LISTEN      41916/python        
tcp        0      0 0.0.0.0:57559           0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:631           0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:8888          0.0.0.0:*               LISTEN      41840/python        
tcp        0      0 127.0.0.1:37561         0.0.0.0:*               LISTEN      41916/python        
tcp        0      0 0.0.0.0:25              0.0.0.0:*               LISTEN      -                   
tcp        0      0 0.0.0.0:33401           0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:38907         0.0.0.0:*               LISTEN      42030/node          
tcp        0      0 127.0.0.1:48571         0.0.0.0:*               LISTEN      41896/gophernotes   
tcp        0      0 127.0.0.1:52347         0.0.0.0:*               LISTEN      41896/gophernotes   
tcp        0      0 127.0.0.1:36893         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 0.0.0.0:57149           0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:40671         0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:37217         0.0.0.0:*               LISTEN      41896/gophernotes   
tcp        0      0 0.0.0.0:2049            0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:43173         0.0.0.0:*               LISTEN      42030/node          
tcp        0      0 127.0.0.1:52133         0.0.0.0:*               LISTEN      41916/python        
tcp        0      0 127.0.0.1:34695         0.0.0.0:*               LISTEN      42030/node          
tcp        0      0 127.0.0.1:33095         0.0.0.0:*               LISTEN      41916/python        
tcp        0      0 127.0.0.1:43113         0.0.0.0:*               LISTEN      41896/gophernotes   
tcp        0      0 127.0.0.1:33291         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 127.0.0.1:33771         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 127.0.0.1:54347         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 127.0.0.1:47819         0.0.0.0:*               LISTEN      41896/gophernotes   
tcp        0      0 127.0.0.1:6379          0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:52781         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 127.0.0.1:45487         0.0.0.0:*               LISTEN      42030/node          
tcp        0      0 127.0.0.1:54895         0.0.0.0:*               LISTEN      42030/node          
tcp        0      0 127.0.0.1:36143         0.0.0.0:*               LISTEN      41916/python        
tcp        0      0 127.0.0.1:35599         0.0.0.0:*               LISTEN      41910/python3       
tcp        0      0 0.0.0.0:111             0.0.0.0:*               LISTEN      -                   
tcp        0      0 127.0.0.1:56817         0.0.0.0:*               LISTEN      41916/python        
tcp6       0      0 :::1716                 :::*                    LISTEN      6607/kdeconnectd    
tcp6       0      0 127.0.0.1:56469         :::*                    LISTEN      41907/java          
tcp6       0      0 :::36533                :::*                    LISTEN      -                   
tcp6       0      0 ::1:53                  :::*                    LISTEN      -                   
tcp6       0      0 :::22                   :::*                    LISTEN      -                   
tcp6       0      0 :::45911                :::*                    LISTEN      -                   
tcp6       0      0 ::1:631                 :::*                    LISTEN      -                   
tcp6       0      0 ::1:8888                :::*                    LISTEN      41840/python        
tcp6       0      0 :::25                   :::*                    LISTEN      -                   
tcp6       0      0 127.0.0.1:43483         :::*                    LISTEN      41907/java          
tcp6       0      0 127.0.0.1:50175         :::*                    LISTEN      41907/java          
tcp6       0      0 127.0.0.1:47391         :::*                    LISTEN      41907/java          
tcp6       0      0 127.0.0.1:46241         :::*                    LISTEN      41907/java          
tcp6       0      0 :::2049                 :::*                    LISTEN      -                   
tcp6       0      0 :::54337                :::*                    LISTEN      -                   
tcp6       0      0 ::1:6379                :::*                    LISTEN      -                   
tcp6       0      0 :::56397                :::*                    LISTEN      -                   
tcp6       0      0 :::111                  :::*                    LISTEN      -                   
udp        0      0 0.0.0.0:4500            0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:37715           0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:5353            0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:38439           0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:47086           0.0.0.0:*                           -                   
udp        0      0 127.0.0.1:53            0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:111             0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:500             0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:631             0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:2049            0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:59513           0.0.0.0:*                           -                   
udp        0      0 0.0.0.0:52130           0.0.0.0:*                           -                   
udp6       0      0 :::45471                :::*                                25836/firefox       
udp6       0      0 :::5353                 :::*                                -                   
udp6       0      0 :::40576                :::*                                -                   
udp6       0      0 :::40772                :::*                                25836/firefox       
udp6       0      0 :::49075                :::*                                25836/firefox       
udp6       0      0 ::1:53                  :::*                                -                   
udp6       0      0 :::111                  :::*                                -                   
udp6       0      0 :::41466                :::*                                -                   
udp6       0      0 :::33275                :::*                                25836/firefox       
udp6       0      0 fe80::857c:b4ed:da2:546 :::*                                -                   
udp6       0      0 :::57901                :::*                                -                   
udp6       0      0 :::1716                 :::*                                6607/kdeconnectd    
udp6       0      0 :::59159                :::*                                -                   
udp6       0      0 :::51185                :::*                                -                   
udp6       0      0 :::2049                 :::*                                -                   
udp6       0      0 :::43268                :::*                                25836/firefox       
udp6       0      0 :::52799                :::*                                25836/firefox       
udp6       0      0 :::53035                :::*                                25836/firefox       

In [12]:

docker ps -a | head

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

CONTAINER ID   IMAGE                                       COMMAND                  CREATED         STATUS                       PORTS                                                            NAMES
26f2be46d51f   5c25aaeaa996                                "/bin/sh -c 'cargo b…"   8 weeks ago     Exited (1) 8 weeks ago                                                                        suspicious_fermat
ba458bfbfb99   be4e3ffba3c1                                "/bin/sh -c 'cargo b…"   8 weeks ago     Exited (101) 8 weeks ago                                                                      competent_lovelace
1edb38cf5c73   d0727d18c097                                "/bin/sh -c 'gradle …"   3 months ago    Exited (1) 3 months ago                                                                       infallible_wozniak
8aa3abeaecd1   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     tender_leavitt
f2ec1d9baa52   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     magical_pare
2d8c65442138   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     practical_tu
a694ad4e6ec3   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     jolly_sutherland
e28e78a99265   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     bold_heisenberg
805e143bd573   8cbaea90e92f                                "java -jar /app/spri…"   3 months ago    Exited (130) 3 months ago                                                                     agitated_ellis

$ kubectl config view

apiVersion: v1
clusters:
- cluster:
    insecure-skip-tls-verify: true
    server: https://35.228.189.126:6443
  name: kubernetes
contexts:
- context:
    cluster: kubernetes
    user: kubernetes-admin
  name: kubernetes-admin@kubernetes
current-context: kubernetes-admin@kubernetes
kind: Config
preferences: {}
users:
- name: kubernetes-admin
  user:
    client-certificate-data: REDACTED
    client-key-data: REDACTED

In [9]:

pwd

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

/home/ryoji/jupyter

In [2]:

mkdir -p "b"

 </div>

In [8]:

cd /home/ryoji/jupyter

 </div>

In [10]:

ln -s b c

 </div>

In [40]:

if [ "$(pwd)" = "/home/ryoji/jupyter" ]
then
    # --include="*/"
    rsync -avh --progress\
    --include="java*.ipynb"\
    --exclude="*" ./ c
fi

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

sending incremental file list
./
java-ryoji-20211025.ipynb
         42.78K 100%    9.55MB/s    0:00:00 (xfr#1, to-chk=1/3)
java.ipynb
         42.78K 100%   40.80MB/s    0:00:00 (xfr#2, to-chk=0/3)
sent 85.78K bytes  received 57 bytes  171.68K bytes/sec
total size is 85.57K  speedup is 1.00

In [41]:

ls b/* -1

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

b/java-ryoji-20211025.ipynb
b/java.ipynb

PDF commands

$ pdfcrop 1300_math_formulas.pdf
$ pdftk 1300_math_formulas-crop.pdf burst
$ for pdf in pg_*.pdf
do
  echo "${pdf##*/}"
  n=$(basename "${pdf##*/}" .pdf)
  convert -density 300 "${pdf}" -resize 36% "png/${n}-%03d.png"
done
$ mogrify -format jpg -background white -alpha remove -alpha off -quality 75%  *.png
$ rename 's/pg_/m1k3-pg_/g' *.jpg
---
$ pdfimages -all -p a.pdf
$ pdftotext a.pdf
$ for png in *.png
do
  echo "${png##*/}"
  tesseract -l eng "${png}" ./eng/"${png##*/}"
done

FFmpeg

$ ffmpeg -i oo3.mp4 -vf scale=700:-1 -r 10 screenshot-3.gif
$ ffplay https://upload.wikimedia.org/wikipedia/commons/transcoded/d/dc/Galton_box.webm/Galton_box.webm.480p.vp9.webm

In [43]:

systemctl status thinkfan

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

● thinkfan.service - simple and lightweight fan control program
     Loaded: loaded (/lib/systemd/system/thinkfan.service; enabled; vendor preset: enabled)
     Active: failed (Result: exit-code) since Tue 2021-10-26 00:23:36 JST; 28min ago
    Process: 1230 ExecStart=/usr/sbin/thinkfan $DAEMON_ARGS (code=exited, status=4)
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwm…tory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwm…tory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwm…tory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwm…tory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwm…tory
Oct 26 00:23:36 ubuntu thinkfan[1230]: readconfig: Error getting temperature.
Oct 26 00:23:36 ubuntu thinkfan[1230]: Refusing to run without usable confi…ile!
Oct 26 00:23:36 ubuntu systemd[1]: thinkfan.service: Control process exited…SION
Oct 26 00:23:36 ubuntu systemd[1]: thinkfan.service: Failed with result 'ex…de'.
Oct 26 00:23:36 ubuntu systemd[1]: Failed to start simple and lightweight f…ram.
Hint: Some lines were ellipsized, use -l to show in full.

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

In [46]:

journalctl -b -u thinkfan --since yesterday

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

-- Logs begin at Sun 2021-10-17 09:31:40 JST, end at Tue 2021-10-26 00:55:36 JST. --
Oct 26 00:23:36 ubuntu systemd[1]: Starting simple and lightweight fan control program...
Oct 26 00:23:36 ubuntu thinkfan[1230]: thinkfan 0.9.1 starting...
Oct 26 00:23:36 ubuntu thinkfan[1230]: WARNING: Using default fan control in /proc/acpi/ibm/fan.
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwmon/hwmon2/temp3_input: No such file or directory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwmon/hwmon2/temp4_input: No such file or directory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwmon/hwmon2/temp1_input: No such file or directory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwmon/hwmon2/temp5_input: No such file or directory
Oct 26 00:23:36 ubuntu thinkfan[1230]: /sys/devices/platform/coretemp.0/hwmon/hwmon2/temp2_input: No such file or directory
Oct 26 00:23:36 ubuntu thinkfan[1230]: readconfig: Error getting temperature.
Oct 26 00:23:36 ubuntu thinkfan[1230]: Refusing to run without usable config file!
Oct 26 00:23:36 ubuntu systemd[1]: thinkfan.service: Control process exited, code=exited, status=4/NOPERMISSION
Oct 26 00:23:36 ubuntu systemd[1]: thinkfan.service: Failed with result 'exit-code'.
Oct 26 00:23:36 ubuntu systemd[1]: Failed to start simple and lightweight fan control program.

In [50]:

crontab -l

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

no crontab for ryoji

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

https://crontab.guru/

In [57]:

cat /etc/fstab | head -n 14 #mount points

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

# /etc/fstab: static file system information.
#
# Use 'blkid' to print the universally unique identifier for a
# device; this may be used with UUID= as a more robust way to name devices
# that works even if disks are added and removed. See fstab(5).
#
# <file system> <mount point>   <type>  <options>       <dump>  <pass>
# / was on /dev/sda5 during installation
UUID=06031935-5dad-47c4-99ee-0bbef6a66588 /               ext4    errors=remount-ro 0       1
# swap was on /dev/sda6 during installation
UUID=19984fa7-4281-4fb4-9297-1c1da6c834d1 none            swap    sw              0       0
# /dev/mapper/cryptswap1 none swap sw 0 0
UUID=c4d2a396-42cc-47ab-8562-9ce100cf6816 /var/lib/docker ext4 defaults,noatime 0 0
UUID=2cade63a-7be9-4b16-9217-46d4b9158d2c /media/dev ext4 defaults,user,noatime,exec 0 0

In [58]:

ifconfig docker0

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

docker0: flags=4099<UP,BROADCAST,MULTICAST>  mtu 1500
        inet 172.17.0.1  netmask 255.255.0.0  broadcast 172.17.255.255
        inet6 fe80::42:60ff:fee7:bde5  prefixlen 64  scopeid 0x20<link>
        ether 02:42:60:e7:bd:e5  txqueuelen 0  (Ethernet)
        RX packets 0  bytes 0 (0.0 B)
        RX errors 0  dropped 0  overruns 0  frame 0
        TX packets 5  bytes 568 (568.0 B)
        TX errors 0  dropped 0 overruns 0  carrier 0  collisions 0

In [59]:

lspci | egrep -i --color 'network|ethernet'

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

00:19.0 Ethernet controller: Intel Corporation 82579LM Gigabit Network Connection (Lewisville) (rev 04)
03:00.0 Network controller: Intel Corporation Centrino Advanced-N 6205 [Taylor Peak] (rev 34)

In [60]:

lshw -class network

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

WARNING: you should run this program as super-user.
  *-network                 
       description: Ethernet interface
       product: 82579LM Gigabit Network Connection (Lewisville)
       vendor: Intel Corporation
       physical id: 19
       bus info: pci@0000:00:19.0
       logical name: enp0s25
       version: 04
       serial: 28:d2:44:44:7d:47
       capacity: 1Gbit/s
       width: 32 bits
       clock: 33MHz
       capabilities: cap_list ethernet physical tp 10bt 10bt-fd 100bt 100bt-fd 1000bt-fd autonegotiation
       configuration: autonegotiation=on broadcast=yes driver=e1000e driverversion=3.2.6-k firmware=0.13-3 latency=0 link=no multicast=yes port=twisted pair
       resources: irq:28 memory:f2500000-f251ffff memory:f253b000-f253bfff ioport:6080(size=32)
  *-network
       description: Wireless interface
       product: Centrino Advanced-N 6205 [Taylor Peak]
       vendor: Intel Corporation
       physical id: 0
       bus info: pci@0000:03:00.0
       logical name: wlp3s0
       version: 34
       serial: a4:4e:31:d1:cd:3c
       width: 64 bits
       clock: 33MHz
       capabilities: bus_master cap_list ethernet physical wireless
       configuration: broadcast=yes driver=iwlwifi driverversion=5.4.0-84-generic firmware=18.168.6.1 ip=192.168.100.102 latency=0 link=yes multicast=yes wireless=IEEE 802.11
       resources: irq:33 memory:f1c00000-f1c01fff
WARNING: output may be incomplete or inaccurate, you should run this program as super-user.

In [63]:

chmod 0700 abc.txt && stat abc.txt\
&& chmod 0664 abc.txt\
&& chmod +x abc.txt && stat abc.txt\
&& chmod -x abc.txt && stat abc.txt

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

  File: abc.txt
  Size: 4         	Blocks: 24         IO Block: 4096   regular file
Device: 3ah/58d	Inode: 10003282    Links: 1
Access: (0700/-rwx------)  Uid: ( 1000/   ryoji)   Gid: ( 1000/   ryoji)
Access: 2021-10-25 21:44:17.157383860 +0900
Modify: 2021-10-25 21:42:38.355751530 +0900
Change: 2021-10-26 01:23:25.824830846 +0900
 Birth: -
  File: abc.txt
  Size: 4         	Blocks: 24         IO Block: 4096   regular file
Device: 3ah/58d	Inode: 10003282    Links: 1
Access: (0775/-rwxrwxr-x)  Uid: ( 1000/   ryoji)   Gid: ( 1000/   ryoji)
Access: 2021-10-25 21:44:17.157383860 +0900
Modify: 2021-10-25 21:42:38.355751530 +0900
Change: 2021-10-26 01:23:25.832831101 +0900
 Birth: -
  File: abc.txt
  Size: 4         	Blocks: 24         IO Block: 4096   regular file
Device: 3ah/58d	Inode: 10003282    Links: 1
Access: (0664/-rw-rw-r--)  Uid: ( 1000/   ryoji)   Gid: ( 1000/   ryoji)
Access: 2021-10-25 21:44:17.157383860 +0900
Modify: 2021-10-25 21:42:38.355751530 +0900
Change: 2021-10-26 01:23:25.836831229 +0900
 Birth: -

In [65]:

chown 1001:1001 abc.txt

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

chown: changing ownership of 'abc.txt': Operation not permitted

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

In [68]:

cat /etc/passwd | head -n 2 #useradd

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

root:x:0:0:root:/root:/bin/bash
daemon:x:1:1:daemon:/usr/sbin:/usr/sbin/nologin

In [3]:

env | sort | tail -7

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

SDKMAN_CANDIDATES_API=https://api.sdkman.io/2
SDKMAN_CANDIDATES_DIR=/home/ryoji/.sdkman/candidates
SDKMAN_DIR=/home/ryoji/.sdkman
SDKMAN_PLATFORM=linuxx64
SDKMAN_VERSION=5.12.4
SHLVL=0
_=/usr/bin/env

In [16]:

export NUM=1;
echo $NUM;

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

1

In [17]:

NUM=2 printenv NUM

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

2

In [18]:

echo $NUM

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

1

In [5]:

ip addr show docker0

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

4: docker0: <NO-CARRIER,BROADCAST,MULTICAST,UP> mtu 1500 qdisc noqueue state DOWN group default 
    link/ether 02:42:c9:ab:88:61 brd ff:ff:ff:ff:ff:ff
    inet 172.17.0.1/16 brd 172.17.255.255 scope global docker0
       valid_lft forever preferred_lft forever

In [5]:

which deno

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

/home/ryoji/.cargo/bin/deno

In [6]:

ps aux | head -n 4

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

USER         PID %CPU %MEM    VSZ   RSS TTY      STAT START   TIME COMMAND
root           1  1.5  0.1 168468 12548 ?        Ss   19:54   0:11 /sbin/init splash
root           2  0.0  0.0      0     0 ?        S    19:54   0:00 [kthreadd]
root           3  0.0  0.0      0     0 ?        I<   19:54   0:00 [rcu_gp]

In [10]:

cat /etc/hosts

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

127.0.0.1        localhost
127.0.1.1        ubuntu
The following lines are desirable for IPv6 capable hosts
::1              localhost ip6-localhost ip6-loopback
ff02::1          ip6-allnodes
ff02::2          ip6-allrouters

In [7]:

dig yahoo.co.jp

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

; <<>> DiG 9.16.1-Ubuntu <<>> yahoo.co.jp
;; global options: +cmd
;; Got answer:
;; ->>HEADER<<- opcode: QUERY, status: NOERROR, id: 37037
;; flags: qr rd ra; QUERY: 1, ANSWER: 8, AUTHORITY: 0, ADDITIONAL: 1
;; OPT PSEUDOSECTION:
; EDNS: version: 0, flags:; udp: 512
;; QUESTION SECTION:
;yahoo.co.jp.			IN	A
;; ANSWER SECTION:
yahoo.co.jp.		163	IN	A	183.79.250.123
yahoo.co.jp.		163	IN	A	182.22.25.124
yahoo.co.jp.		163	IN	A	182.22.25.252
yahoo.co.jp.		163	IN	A	183.79.219.252
yahoo.co.jp.		163	IN	A	183.79.217.124
yahoo.co.jp.		163	IN	A	182.22.16.251
yahoo.co.jp.		163	IN	A	183.79.250.251
yahoo.co.jp.		163	IN	A	182.22.28.252
;; Query time: 80 msec
;; SERVER: 192.168.100.1#53(192.168.100.1)
;; WHEN: Thu Oct 28 20:15:43 JST 2021
;; MSG SIZE  rcvd: 168

• https://docs.microsoft.com/en-us/azure/dns/dns-getstarted-portal

In [13]:

docker network inspect bridge

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

[
    {
        "Name": "bridge",
        "Id": "af34c9cd68d18c2ac326c6faded174f7f45685d3d0f7ec488bc7be9722cd3556",
        "Created": "2021-10-28T19:55:05.352829424+09:00",
        "Scope": "local",
        "Driver": "bridge",
        "EnableIPv6": false,
        "IPAM": {
            "Driver": "default",
            "Options": null,
            "Config": [
                {
                    "Subnet": "172.17.0.0/16",
                    "Gateway": "172.17.0.1"
                }
            ]
        },
        "Internal": false,
        "Attachable": false,
        "Ingress": false,
        "ConfigFrom": {
            "Network": ""
        },
        "ConfigOnly": false,
        "Containers": {},
        "Options": {
            "com.docker.network.bridge.default_bridge": "true",
            "com.docker.network.bridge.enable_icc": "true",
            "com.docker.network.bridge.enable_ip_masquerade": "true",
            "com.docker.network.bridge.host_binding_ipv4": "0.0.0.0",
            "com.docker.network.bridge.name": "docker0",
            "com.docker.network.driver.mtu": "1500"
        },
        "Labels": {}
    }
]

In [16]:

ip route

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

default via 192.168.100.1 dev wlp3s0 proto dhcp metric 600 
169.254.0.0/16 dev wlp3s0 scope link metric 1000 
172.17.0.0/16 dev docker0 proto kernel scope link src 172.17.0.1 linkdown 
172.18.0.0/16 dev br-e1604f91b0da proto kernel scope link src 172.18.0.1 linkdown 
172.19.0.0/16 dev br-e4a69edd1eb4 proto kernel scope link src 172.19.0.1 linkdown 
172.20.0.0/16 dev br-d89fe5f13325 proto kernel scope link src 172.20.0.1 linkdown 
172.21.0.0/16 dev br-6d2f1b776d01 proto kernel scope link src 172.21.0.1 linkdown 
172.22.0.0/16 dev br-17ceecb1cb0a proto kernel scope link src 172.22.0.1 
192.168.100.0/24 dev wlp3s0 proto kernel scope link src 192.168.100.102 metric 600 

ryoji@ubuntu:~$ sudo iptables -L
Chain DOCKER (6 references)
target     prot opt source               destination

ACCEPT     tcp  --  anywhere             172.22.0.2           tcp dpt:4444
ACCEPT     tcp  --  anywhere             172.22.0.3           tcp dpt:5900

In [17]:

docker ps

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

CONTAINER ID   IMAGE                                COMMAND                  CREATED              STATUS              PORTS                    NAMES
b9a94b4a9211   selenium/node-chrome-debug:3.141.0   "/opt/bin/entry_poin…"   About a minute ago   Up About a minute   0.0.0.0:5900->5900/tcp   selenium_chrome-node_1
557f254f7ffe   selenium/hub:3.141.0                 "/opt/bin/entry_poin…"   About a minute ago   Up About a minute   0.0.0.0:4444->4444/tcp   selenium_selenium-hub_1

ryoji@ubuntu:~$ ping 172.21.0.1
PING 172.21.0.1 (172.21.0.1) 56(84) bytes of data.
64 bytes from 172.21.0.1: icmp_seq=1 ttl=64 time=0.108 ms
64 bytes from 172.21.0.1: icmp_seq=2 ttl=64 time=0.090 ms
^C
--- 172.21.0.1 ping statistics ---
2 packets transmitted, 2 received, 0% packet loss, time 1014ms
rtt min/avg/max/mdev = 0.090/0.099/0.108/0.009 ms
ryoji@ubuntu:~$ ping 172.22.0.1
PING 172.22.0.1 (172.22.0.1) 56(84) bytes of data.
64 bytes from 172.22.0.1: icmp_seq=1 ttl=64 time=0.114 ms
^C
--- 172.22.0.1 ping statistics ---
1 packets transmitted, 1 received, 0% packet loss, time 0ms
rtt min/avg/max/mdev = 0.114/0.114/0.114/0.000 ms
ryoji@ubuntu:~$ ping 172.22.0.2
PING 172.22.0.2 (172.22.0.2) 56(84) bytes of data.
64 bytes from 172.22.0.2: icmp_seq=1 ttl=64 time=0.112 ms
^C
--- 172.22.0.2 ping statistics ---
2 packets transmitted, 2 received, 0% packet loss, time 1029ms
rtt min/avg/max/mdev = 0.101/0.106/0.112/0.005 ms
ryoji@ubuntu:~$ ping 172.22.0.3
PING 172.22.0.3 (172.22.0.3) 56(84) bytes of data.
64 bytes from 172.22.0.3: icmp_seq=1 ttl=64 time=0.087 ms
^C
--- 172.22.0.3 ping statistics ---
3 packets transmitted, 3 received, 0% packet loss, time 2030ms
rtt min/avg/max/mdev = 0.087/0.099/0.111/0.009 ms
ryoji@ubuntu:~$ ping 172.22.0.4
PING 172.22.0.4 (172.22.0.4) 56(84) bytes of data.
From 172.22.0.1 icmp_seq=1 Destination Host Unreachable
^C
--- 172.22.0.4 ping statistics ---
4 packets transmitted, 0 received, +3 errors, 100% packet loss, time 3062ms
pipe 4

In [18]:

id

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

uid=1000(ryoji) gid=1000(ryoji) groups=1000(ryoji),4(adm),24(cdrom),27(sudo),30(dip),46(plugdev),113(lpadmin),128(sambashare),131(kvm),132(ubridge),133(libvirtd),145(wireshark),991(microk8s),997(docker)

kind: ConfigMap
apiVersion: v1
metadata:
  name: config
  namespace: metallb-system
data:
  config: |
    address-pools:
    - name: default
      protocol: layer2
      addresses:
      - 192.168.49.50 - 192.168.49.60

In [24]:

ip route

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

default via 192.168.100.1 dev wlp3s0 proto dhcp metric 600 
169.254.0.0/16 dev wlp3s0 scope link metric 1000 
172.17.0.0/16 dev docker0 proto kernel scope link src 172.17.0.1 linkdown 
192.168.49.0/24 dev br-9384eda79fdc proto kernel scope link src 192.168.49.1 
192.168.99.0/24 dev vboxnet2 proto kernel scope link src 192.168.99.1 linkdown 
192.168.100.0/24 dev wlp3s0 proto kernel scope link src 192.168.100.102 metric 600 

Network Address Port Translation¶

ryoji@ubuntu:~$ sudo iptables -L
Chain DOCKER (2 references)
target     prot opt source               destination         
ACCEPT     tcp  --  anywhere             192.168.49.2         tcp dpt:32443
ACCEPT     tcp  --  anywhere             192.168.49.2         tcp dpt:8443
ACCEPT     tcp  --  anywhere             192.168.49.2         tcp dpt:5000
ACCEPT     tcp  --  anywhere             192.168.49.2         tcp dpt:2376
ACCEPT     tcp  --  anywhere             192.168.49.2         tcp dpt:ssh

Classless Inter-Domain Routing¶

• docs.microsoft.com/en-us/azure/vpn-gateway/tutorial-create-gateway-portal#CreatVNet
• VPN tunnel IPSec
• docs.aws.amazon.com/en_en/vpc/latest/userguide/vpc-nat-gateway.html

gateway & router¶

$ mtr yahoo.co.jp

In [1]:

nslookup speedwifi-next.home

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

;; Got recursion not available from 192.168.100.1, trying next server
Server:		fe80::8a10:8fff:fe5a:2ebb%3%3
Address:	fe80::8a10:8fff:fe5a:2ebb%3#53
Non-authoritative answer:
Name:	speedwifi-next.home
Address: 192.168.100.1
;; Got recursion not available from 192.168.100.1, trying next server
Name:	speedwifi-next.home
Address: fe80::8a10:8fff:fe5a:2ebb

In [1]:

netstat --route

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

Kernel IP routing table
Destination     Gateway         Genmask         Flags   MSS Window  irtt Iface
default         speedwifi-next. 0.0.0.0         UG        0 0          0 wlp3s0
link-local      0.0.0.0         255.255.0.0     U         0 0          0 wlp3s0
172.17.0.0      0.0.0.0         255.255.0.0     U         0 0          0 docker0
192.168.49.0    0.0.0.0         255.255.255.0   U         0 0          0 br-9384eda79fdc
192.168.100.0   0.0.0.0         255.255.255.0   U         0 0          0 wlp3s0

In [3]:

route | grep wlp3s0

 </div>

<div class="jp-OutputPrompt jp-OutputArea-prompt"></div>

default         speedwifi-next. 0.0.0.0         UG    600    0        0 wlp3s0
link-local      0.0.0.0         255.255.0.0     U     1000   0        0 wlp3s0
192.168.100.0   0.0.0.0         255.255.255.0   U     600    0        0 wlp3s0

For example, add NAPT settings that let it go from the internet to a server with a local address.

Find the global address of the gateway.

• https://www.myglobalip.com/
• http://inet-ip.info/

Theoretically this request will be forwarded to port 22 of one of my docker services.

ssh -p 34567 user@111.239.178.96

kubernetes CoreDNS¶

Other stuff¶

ryoji@ubuntu:~$ sudo pmap 36900
36900:   w
00005567d18f5000     32K r---- w
00005567d18fd000    336K r-x-- w
00005567d1951000  43388K r---- w
00005567d43b0000     20K r---- w
00005567d43b5000      4K rw--- w
00005567d4499000  47088K rw---   [ anon ]
00007f28b5e68000   6148K rw---   [ anon ]
00007f28b6469000   3076K rw---   [ anon ]
00007f28b6a0d000      8K rw---   [ anon ]
00007f28b6a0f000    148K r---- libc-2.31.so
00007f28b6a34000   1504K r-x-- libc-2.31.so
00007f28b6bac000    296K r---- libc-2.31.so
00007f28b6bf6000      4K ----- libc-2.31.so
00007f28b6bf7000     12K r---- libc-2.31.so
00007f28b6bfa000     12K rw--- libc-2.31.so
00007f28b6bfd000     16K rw---   [ anon ]
00007f28b6c01000      4K r---- libdl-2.31.so
00007f28b6c02000      8K r-x-- libdl-2.31.so
00007f28b6c04000      4K r---- libdl-2.31.so
00007f28b6c05000      4K r---- libdl-2.31.so
00007f28b6c06000      4K rw--- libdl-2.31.so
00007f28b6c07000     60K r---- libm-2.31.so
00007f28b6c16000    668K r-x-- libm-2.31.so
00007f28b6cbd000    604K r---- libm-2.31.so
00007f28b6d54000      4K r---- libm-2.31.so
00007f28b6d55000      4K rw--- libm-2.31.so
00007f28b6d56000     28K r---- libpthread-2.31.so
00007f28b6d5d000     68K r-x-- libpthread-2.31.so
00007f28b6d6e000     20K r---- libpthread-2.31.so
00007f28b6d73000      4K r---- libpthread-2.31.so
00007f28b6d74000      4K rw--- libpthread-2.31.so
00007f28b6d75000     16K rw---   [ anon ]
00007f28b6d79000     12K r---- libgcc_s.so.1
00007f28b6d7c000     72K r-x-- libgcc_s.so.1
00007f28b6d8e000     16K r---- libgcc_s.so.1
00007f28b6d92000      4K r---- libgcc_s.so.1
00007f28b6d93000      4K rw--- libgcc_s.so.1
00007f28b6d94000      8K rw---   [ anon ]
00007f28b6dc8000      4K -----   [ anon ]
00007f28b6dc9000      8K rw---   [ anon ]
00007f28b6dcb000      4K r---- ld-2.31.so
00007f28b6dcc000    140K r-x-- ld-2.31.so
00007f28b6def000     32K r---- ld-2.31.so
00007f28b6df8000      4K r---- ld-2.31.so
00007f28b6df9000      4K rw--- ld-2.31.so
00007f28b6dfa000      4K rw---   [ anon ]
00007ffc0eb38000    136K rw---   [ stack ]
00007ffc0eba1000     12K r----   [ anon ]
00007ffc0eba4000      4K r-x--   [ anon ]
ffffffffff600000      4K --x--   [ anon ]
 total           104068K

ryoji@ubuntu:~$ ldd .local/bin/w
    linux-vdso.so.1 (0x00007ffd61da7000)
    libgcc_s.so.1 => /lib/x86_64-linux-gnu/libgcc_s.so.1 (0x00007f624afe2000)
    libpthread.so.0 => /lib/x86_64-linux-gnu/libpthread.so.0 (0x00007f624afbf000)
    libm.so.6 => /lib/x86_64-linux-gnu/libm.so.6 (0x00007f624ae70000)
    libdl.so.2 => /lib/x86_64-linux-gnu/libdl.so.2 (0x00007f624ae6a000)
    libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007f624ac78000)
    /lib64/ld-linux-x86-64.so.2 (0x00007f624daf5000)

In [ ]:

 </div>

public class HelloWorld {
    public static void main(String[] args) {
        System.out.println("Hello, World");
    }
}

public class HelloGoodbye {
    public static void main(String[] args) {
        System.out.println("Hello " + args[0] + " and " + args[1] + ".");
        System.out.println("Goodbye " + args[1] + " and " + args[0] + ".");
    }
}

import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdRandom;

public class RandomWord {
    public static void main(String[] args) {
        int idx = 1;
        String champ = "";
        while (!StdIn.isEmpty()) {
            String word = StdIn.readString();
            double odds = 1.0D / idx;
            boolean isWinner = StdRandom.bernoulli(odds);
            if (isWinner) {
                champ = word;
            }
            idx++;
        }
        StdOut.println(champ);
    }
}

coursera/src$ zip -r hello.zip HelloGoodbye.java HelloWorld.java RandomWord.java
updating: HelloGoodbye.java (deflated 44%)
updating: HelloWorld.java (deflated 19%)
updating: RandomWord.java (deflated 65%)

coursera/src$ CLASSPATH=../algs4.jar javac RandomWord.java
coursera/src$ CLASSPATH=.:../algs4.jar java RandomWord
# in my environment, `while (!StdIn.isEmpty())` didn't stop

---

The following code was not allowed.

Checkstyle ends with 5 errors.
[ERROR] RandomWord.java:6:5: Do not declare instance variables in this program. [NothingButMain]
[ERROR] RandomWord.java:7:5: Do not declare instance variables in this program. [NothingButMain]
[ERROR] RandomWord.java:9:5: Do not define instance methods in this program. [NothingButMain]
[ERROR] RandomWord.java:18:5: Do not define instance methods in this program. [NothingButMain]
[ERROR] RandomWord.java:38:25: Do not create arrays (or other objects) with 'new' in this program. [Design]

/**
 * RandomWordSelector selects one of the words, which are fed sequentially, in a real-time manner.
 */
class RandomWordSelector {
    private int consumptionCount;
    private String selection;

    public void consume(String word) {
        double odds = 1.0D / (consumptionCount + 1);
        boolean retain = StdRandom.bernoulli(odds);
        if (retain) {
            selection = word;
        }
        consumptionCount++;
    }

    public String getSelection() {
        return selection;
    }
}

public class RandomWord {
    public static void main(String[] args) {
        RandomWordSelector rws = new RandomWordSelector();
        while (!StdIn.isEmpty()) {
            rws.consume(StdIn.readString());
        }
        StdOut.println(rws.getSelection());
    }
}

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to Maclaurin series approximation

1. Brute force

use std::time::Instant;

fn square_root_brute(aa: u32) -> u32 {
    let mut a = 0u32;
    while a as u64 * a as u64 <= aa as u64 {
        a += 1;
    }
    a - 1
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_brute(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_brute(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to Maclaurin series approximation

2. Newton's method

• https://tour.golang.org/flowcontrol/8

use std::time::Instant;

fn square_root_newton(a: u32) -> u32 {
    let mut x = 1f32;
    let mut x_next: f32;
    loop {
        x_next = (x + a as f32 / x) / 2f32;
        if (x - x_next).abs() < 0.1 {
            break x_next as u32;
        }
        x = x_next;
    }
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f32).sqrt() as u32, square_root_newton(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f32).sqrt() as u32, square_root_newton(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

use std::time::Instant;

fn square_root_newton(a: u32) -> u32 {
    let mut x = 1f64;
    let mut x_next: f64;
    loop {
        x_next = (x + a as f64 / x) / 2f64;
        if (x - x_next).abs() < 0.1 {
            break x_next as u32;
        }
        x = x_next;
    }
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_newton(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_newton(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

use std::time::Instant;

fn square_root_newton(a: u32) -> u32 {
    let mut x = 1u64;
    let mut x_next: u64;
    loop {
        x_next = (x + a as u64 / x) / 2;
        if x == x_next || x_next * x_next <= a as u64 {
            break x_next as u32;
        }
        x = x_next;
    }
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_newton(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_newton(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

• The Go Playground

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to Maclaurin series approximation

3. Digit-by-digit calculation

use std::time::Instant;

fn subtract_largest_block_from_carry(carry: &mut u32, divisor: &mut u32, x: &mut u32) {
    for i in (0u32..10).rev() {
        let block = (*divisor + i) * i;
        if block > *carry {
            continue;
        }
        *carry -= block;
        *divisor += i * 2;
        *x += i;
        break;
    }
}

fn square_root_digit_by_digit(mut a: u32) -> u32 {
    let mut digits = vec![];
    while a > 0 {
        digits.push(a % 100);
        a /= 100;
    }
    let (mut x, mut divisor, mut carry) = (0u32, 0u32, 0u32);
    for &n in digits.iter().rev() {
        carry = carry * 100 + n;
        divisor *= 10;
        x *= 10;
        subtract_largest_block_from_carry(&mut carry, &mut divisor, &mut x);
    }
    x
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_digit_by_digit(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_digit_by_digit(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

use std::time::Instant;

fn square_root_digit_by_digit(mut a: u32) -> u32 {
    let mut x = 0u32;
    let mut bit: u32 = 0b01000000000000000000000000000000;
    while bit > a {
        bit >>= 2;
    }
    while bit != 0 {
        let block = x + bit;
        x >>= 1;
        if a >= block {
            a -= block;    
            x += bit;
        }
        bit >>= 2;
    }
    x
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_digit_by_digit(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_digit_by_digit(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to Maclaurin series approximation

4. Bisection method

use std::time::Instant;
use std::cmp::Ordering;

fn square_root_bisection(a: u32) -> u32 {
    let (mut top, mut bottom) = (a.clone() as f64, 0f64);
    loop {
        if top - bottom < 0.00001 {
            break top as u32;
        }
        let median = bottom + (top - bottom) / 2f64;
        match (&(a as f64)).partial_cmp(&(median * median)).unwrap() {
            Ordering::Less => top = median,
            Ordering::Equal => return median as u32,
            Ordering::Greater => bottom = median,
        }
    }
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        assert_eq!((i as f64).sqrt() as u32, square_root_bisection(i));
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        assert_eq!((i as f64).sqrt() as u32, square_root_bisection(i));
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to Maclaurin series approximation

5. Maclaurin series approximation

It's also applicable for logarithm

• L.69 Square root
• Q.42 Coded triangle numbers

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

1. Brute force

use std::time::Instant;

fn is_perfect_square_brute(aa: u32) -> bool {
    if aa == 0 || aa == 1 {
        return true;
    }
    for a in 0u64..=aa as u64 / 2 {
        let square = a * a;
        if square == aa as u64 {
            return true;
        }
        if square > aa as u64 {
            return false;
        }
    }
    false
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_brute(i), "{}", i);
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_brute(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

2. Newton's method

use std::time::Instant;

fn is_perfect_square_newton(a: u32) -> bool {
    let mut x = a / 2 + 1;
    while x as u64 * x as u64 > a as u64 {
        x = (a / x + x) / 2;
    }
    x * x == a
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_newton(i), "{}", i);
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_newton(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

3. Digit-by-digit calculation

use std::time::Instant;

fn is_perfect_square_digit_by_digit(mut a: u32) -> bool {
    let mut x = 0u32;
    let mut bit: u32 = 0b01000000000000000000000000000000;
    while bit > a {
        bit >>= 2;
    }
    while bit != 0 {
        let block = x + bit;
        x >>= 1;
        if a >= block {
            a -= block;
            x += bit;
        }
        bit >>= 2;
    }
    a == 0
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_digit_by_digit(i), "{}", i);
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_digit_by_digit(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

4. Bisection method

use std::time::Instant;
use std::cmp::Ordering;

fn is_perfect_square_bisection(a: u32) -> bool {
    let (mut top, mut bottom) = (a.clone(), 0u32);
    while bottom <= top {
        let median = bottom + (top - bottom) / 2;
        match (&(a as u64))
            .partial_cmp(&(median as u64 * median as u64))
            .unwrap()
        {
            Ordering::Less => top = median - 1,
            Ordering::Equal => return true,
            Ordering::Greater => bottom = median + 1,
        }
    }
    false
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..100 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_bisection(i), "{}", i);
    }
    for i in 2_147_395_500u32..2_147_395_601 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_bisection(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

5. Number of divisors

• Q.12 Highly divisible triangular number

use std::time::Instant;

fn rule_out(sieve: &mut Vec<bool>, prime: usize) {
    for i in (prime * prime..sieve.len()).step_by(prime) {
        sieve[i] = false;
    }
}

fn primes(below: u32) -> Vec<u32> {
    match below {
        0 | 1 | 2 => return vec![],
        3 => return vec![2],
        _ => (),
    }
    let mut primes: Vec<u32> = vec![2u32, 3u32];
    let mut sieve = vec![true; below as usize];
    let mut index = 5usize;
    let mut ite = [2usize, 4].iter().cycle();
    while index * index < below as usize {
        if sieve[index] {
            primes.push(index as u32);
            rule_out(&mut sieve, index);
        }
        index += ite.next().unwrap();
    }
    while index < sieve.len() {
        if sieve[index] {
            primes.push(index as u32);
        }
        index += ite.next().unwrap();
    }
    primes
}

fn num_of_divisors(mut n: u32) -> u64 {
    let mut count = 1u64;
    for &p in &primes(n + 1) {
        if n % p != 0 {
            continue;
        }
        let mut exp = 0u64;
        while {
            n /= p;
            exp += 1;
            n % p == 0
        } {}
        count *= exp + 1;
    }
    count
}

pub fn is_perfect_square_prime(a: u32) -> bool {
    num_of_divisors(a) % 2 == 1
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..1_000 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_prime(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

---

• 1. Go to a brute force solution
• 2. Go to Newton's method aka. Babylonian method solutions
• 3. Go to digit-by-digit calculation solutions
• 4. Go to a bisection method solution
• 5. Go to a number of divisor function proposal
• 6. Go to a difference sequence proposal

6. Difference sequence

use std::time::Instant;

fn is_perfect_square_difference_sequence(a: u32) -> bool {
    let mut sum = 0u32;
    for i in (1..).step_by(2) {
        if sum == a {
            return true;
        }
        sum += i;
        if sum > a {
            break;
        }
    }
    false
}

fn main() {
    let timer = Instant::now();
    for i in 0u32..10_000 {
        let sqrt = (i as f64).sqrt() as u32;
        assert_eq!(sqrt * sqrt == i, is_perfect_square_difference_sequence(i), "{}", i);
    }
    println!("Time elapsed {:?}", timer.elapsed());
}

I'd like to pick up four famous bugs that are hard to detect.

1. Let's Encrypt, loop with reference

• bugzilla.mozilla.org/show_bug.cgi?id=1619047

Something that the compiler should detect. But the compiler can't tell if it's an illegal practice or just a clever hack to update values in place.

&vs converge into one single address.

func authzModelMapToPB(m map[string]authzModel) (*apb.Authorizations, error) {
        resp := &apb.Authorizations{}
        for k, v := range m {
                // Make a copy of k because it will be reassigned with each loop.
                kCopy := k
                authzPB, err := modelToAuthzPB(&v)
                if err != nil {
                        return nil, err
                }
                resp.Authz = append(resp.Authz, &apb.Authorizations_MapElement{Domain: &kCopy, Authz: authzPB})
        }
        return resp, nil
}

• github.com/golang/go/wiki/CommonMistakes#using-reference-to-loop-iterator-variable

package main

import "fmt"

func main() {
	var out []*int
	for i := 0; i < 3; i++ {
		out = append(out, &i)
	}
	fmt.Println("Values:", *out[0], *out[1], *out[2])
	fmt.Println("Addresses:", out[0], out[1], out[2])
	// Values: 3 3 3
	// Addresses: 0xc000126000 0xc000126000 0xc000126000
}

package main

import (
	"fmt"
)

func main() {
	set := map[int]bool{}
	set[175] = true
	set[119] = false
	set[450] = true

	fmt.Println(set)
	for k, v := range set {
		fmt.Println(&k, k, &v, v)
	}
	// map[119:false 175:true 450:true]
	// 0xc000018068 175 0xc000018080 true
	// 0xc000018068 119 0xc000018080 false
	// 0xc000018068 450 0xc000018080 true
}

In Rust, for loop is a "consumer" by default. That is very confusing at a first look.

use std::collections::HashMap;

fn consuming_iter() {
    let m = HashMap::from([(123, true), (456, false), (789, true)]);
    println!("{:p}", &m);
    for (k, v) in m.into_iter() {
        println!("{}\t{:p}\t{}\t{:p}", k, &k, v, &v);
    }
    // println!("{:?}", m) value borrowed here after move error
}

fn consuming_iter_to_be_called() {
    let m = HashMap::from([(123, true), (456, false), (789, true)]);
    println!("{:p}", &m);
    // "for _ in m" is a syntax sugar for m.into_iter()
    for (k, v) in m {
        println!("{}\t{:p}\t{}\t{:p}", k, &k, v, &v);
    }
    // println!("{:?}", m) value borrowed here after move error
}

fn non_consuming_iter() {
    let m = HashMap::from([(123, true), (456, false), (789, true)]);
    println!("{:p}", &m);
    for (k, v) in m.iter() {
        println!("{}\t{:p}\t{}\t{:p}", k, k, v, v);
        // println!("{}\t{:p}\t{}\t{:p}", *k, k, *v, v); // same. explicit dereferencing
    }
    println!("{:?}", m)
}

fn non_consuming_iter_to_be_called() {
    let m = HashMap::from([(123, true), (456, false), (789, true)]);
    println!("{:p}", &m);
    // "for _ in &m" is a syntax sugar for .iter()
    for (k, v) in &m {
        println!("{}\t{:p}\t{}\t{:p}", k, k, v, v);
        // println!("{}\t{:p}\t{}\t{:p}", *k, k, *v, v); // same. explicit dereferencing
    }
    println!("{:?}", m)
}

fn main() {
    // same address of a value in loop
    consuming_iter();
    consuming_iter_to_be_called();
    println!("---");
    // the original addresses of the values in map
    non_consuming_iter();
    non_consuming_iter_to_be_called();
}

// 0x7ffc7da2ff30 <- frame of map struct in stack pointing to actual values in heap
// 789	0x7ffc7da2feac	true	0x7ffc7da2fe1f <- value copied to stack
// 123	0x7ffc7da2feac	true	0x7ffc7da2fe1f <- value copied to stack
// 456	0x7ffc7da2feac	false	0x7ffc7da2fe1f <- value copied to stack
// 0x7ffc7da2ff30 <- frame of map struct in stack pointing to actual values in heap
// 123	0x7ffc7da2feac	true	0x7ffc7da2fe1f <- value copied to stack
// 456	0x7ffc7da2feac	false	0x7ffc7da2fe1f <- value copied to stack
// 789	0x7ffc7da2feac	true	0x7ffc7da2fe1f <- value copied to stack
// ---
// 0x7ffc7da2feb0 <- frame of map struct in stack pointing to actual values in heap
// 456	0x562b9bf4ac98	false	0x562b9bf4ac9c <- value in heap
// 123	0x562b9bf4ac88	true	0x562b9bf4ac8c <- value in heap
// 789	0x562b9bf4ac80	true	0x562b9bf4ac84 <- value in heap
// {456: false, 123: true, 789: true}
// 0x7ffc7da2feb0 <- frame of map struct in stack pointing to actual values in heap
// 456	0x562b9bf4ac98	false	0x562b9bf4ac9c <- value in heap
// 123	0x562b9bf4ac90	true	0x562b9bf4ac94 <- value in heap
// 789	0x562b9bf4ac88	true	0x562b9bf4ac8c <- value in heap
// {456: false, 123: true, 789: true}

---

• wantedly.com/companies/wantedly/post_articles/290761 (Japanese)

In a sense, it's working like the union type of C that enables the sharing of the same memory address between different things.

package main

import "fmt"

func main() {
	slice := []int{2, 2, 5, 3, 6, 9, 2}
	fmt.Println("original =", slice)
	// original = [2 2 5 3 6 9 2]
	filtered := slice[:0]
	for _, elem := range slice {
		if elem%2 == 0 {
			filtered = append(filtered, elem)
		}
	}
	fmt.Println("filtered =", filtered)
	fmt.Println("original =", slice)
	// filtered = [2 2 6 2]
	// original = [2 2 6 2 6 9 2]
}

In some other languages, immutability resolves this difficulty.

public static void main(String[] args) {
    List<String> list = new ArrayList<String>();
    list.add("A");
    list.add("B");
    list.add("C");
    for (String str : list) {
        if ("B".equals(str)) {
            // ConcurrentModificationException
            list.remove(str);
        }
    }
}

2. Chrome OS, typo in log-in condition && and &

• news.ycombinator.com/item?id=27922545

if (key_data_.has_value() && !key_data_->label().empty()) {}
if (key_data_.has_value() & !key_data_->label().empty()) {}

In modern languages, except for javascript, 0 1 and false true are segregated. It's more dangerous than convenient.

3. log4j, composition of functionalities

Due to the combinatorial explosion and the devil's proof, you can't say there surely won't be a new combination of functionalities in the uncertain future that introduces a critical bug to the ecosystem.

In software engineering, "the single-responsibility principle" is heuristically known to tackle this difficulty. It's what's called Unix philosophy: 'Make each program do one thing well. To do a new job, build afresh rather than complicate old programs by adding new "features".'

A downside of microservice architecture is that it's beyond the checking mechanism of compilers, like Regular Expression itself is a powerful language so that it comes with both flexibility and unpredictability. Integration testing and debugging often become harder. Please read this with a grain of salt because perhaps I'm wrong, but I recalled the Linux victory over GNU Hurd of microkernel and the controversies over the conglomerate systemd architecture.

4. Hewlett-Packard, data loss incident - backup Ops with shell script

• bot.rnewshub.com/77tb-of-kyoto-university-supercomputer-information-lacking-because-of-bug-in-hp-japan-pc-watch-software-program/

The back-up operation was written in a shell script which contained the find command and some bash functions. It was during the operation. The shell script was overwitten with a newer version of the code, which caused the hot reloading by the sh process. The Unix shell interpreter returned an empty string '' as one of bash functions became undefined or one of variables get cleared, and the succeeding procedure executed the delete command on the root of directory subtree.

A direct protective measure was the writing of the code in a compiler language such as C, Rust, and Go but not in Bash. An example is rustup. This installer itself is written in Rust. Writing an extensive application in something like Bash or AWK can be abusive. But it's not the nitty-gritty.

Systematic approach is more conservative, and it's recommended to backup addition-wise with generation info like the way git keeps the full development history. But it's expensive.

Another problem is the locking or things like the garbage collector's Stop The World. Keep observing and applying changes on an ever-changing system is not easy stuff. If possible, it's preferred to make the transition from system-wide approaches to the ones having the nature of divide-and-conquer with lock as keeping atomicity and consistency.

(to talk about this incident specifically and the cheapest way of prevention, they should have started the Bash process as a special user purposely created who didn't have the permission to modify files anywhere but in logs. thus this data loss could be averted by the permission denial of the OS as a fail-safe measure.)

P.S. for 1. Let's Encrypt, loop with reference

It's very often a bad practice not to use the pass-by-value feature in Go which is the default mode of the language.

package main

import (
	"fmt"
)

func coalesce(v *bool, zero *interface{}) interface{} {
	if v != nil {
		return *v
	}
	return *zero
}

func main() {
	set := map[int]*bool{}
	a, b, c, d := 175, 119, 450, 999
	yes, no := true, false
	set[a] = &yes
	set[b] = &no
	set[c] = &yes
	set[d] = nil

	fmt.Println(set)
	for k, v := range set {
		fmt.Println(&k, k, v, coalesce(v, new(interface{})))
	}
	// map[119:0xc000126001 175:0xc000126000 450:0xc000126000 999:<nil>]
	// 0xc000126030 119 0xc000126001 false
	// 0xc000126030 450 0xc000126000 true
	// 0xc000126030 999 <nil> <nil>
	// 0xc000126030 175 0xc000126000 true
}

---

Off topic but initialization in Go can be confusing at a glance.

• Difference between var, new and :=

package main

import (
	"fmt"
	"unsafe"
)

func Example() {
	fmt.Println("make([]int, 0) -> not nil")
	if slice := make([]int, 0); slice != nil {
		fmt.Println(unsafe.Sizeof(slice))
		slice = append(slice, 1)
	}
	fmt.Println("new([]int) -> pointer to nil")
	if slice := new([]int); *slice == nil {
		fmt.Println(unsafe.Sizeof(*slice))
		*slice = append(*slice, 1)
	}
	fmt.Println("var slice []int -> nil")
	var slice []int
	if slice == nil {
		fmt.Println(unsafe.Sizeof(slice))
		slice = append(slice, 1)
	}
	// Output:
	// make([]int, 0) -> not nil
	// 24
	// new([]int) -> pointer to nil
	// 24
	// var slice []int -> nil
	// 24
}

This website is a collection of Ryoji's memos in github.com/growingspaghetti/project-euler as the scrapbox.